Skip to main content
LibreTexts - Ukrayinska

8.17: Композитні перетворення

  1. Last updated
  2. Save as PDF
  • Page ID
    54925

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Дізнайтеся, як складати перетворення фігури на координатній площині, і зрозумійте порядок їх застосування.

    Резюме перетворень

    Трансформація - це операція, яка рухає, перевертає або іншим чином змінює фігуру для створення нової фігури. Жорстке перетворення (також відоме як ізометрія або перетворення конгруентності) - це трансформація, яка не змінює розмір або форму фігури. Нова фігура, створена перетворенням, називається зображенням. Оригінальна фігура називається передзображенням.

    Існує три жорстких перетворення: переклади, обертання і роздуми. Переклад - це перетворення, яке переміщує кожну точку фігури на однакову відстань в одному напрямку. Обертання - це перетворення, коли фігура обертається навколо фіксованої точки для створення зображення. Відображення - це перетворення, яке перетворює фігуру в її дзеркальне відображення, перевертаючи її над лінією.

    Склад перетворень

    Композиція (перетворень) - це коли на фігурі виконується більше одного перетворення. Твори завжди можна написати за одним правилом. Скласти можна будь-які перетворення, але ось кілька найпоширеніших композицій:

    1. Відбиття ковзання - це композиція рефлексії та перекладу. Переклад відбувається в напрямку, паралельному лінії відображення.

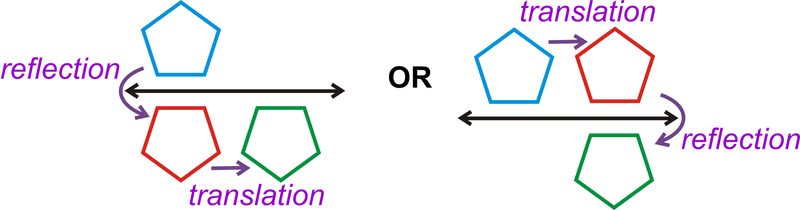
    F-д_Д9Б3А436Е15470 ДБ9653Б3Б3Б3С0824936А10А39752КС4617Е1ДК057+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)
    1. Склад двох відображень над паралельними лініями, які є\(h\) одиницями один від одного, такий же, як і переклад\(2h\) одиниць (Теорема про роздуми над паралельними лініями).
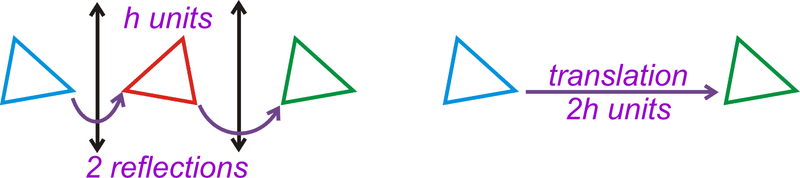
    F-д_6д6645aafb3a96521e804a784f570ЕС7 БББ 8900A5CE381F17A2C32+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Якщо скласти два відображення над кожною віссю, то остаточне зображення - це обертання\(180^{\circ}\) навколо початку оригіналу (Відображення над теоремою осей).

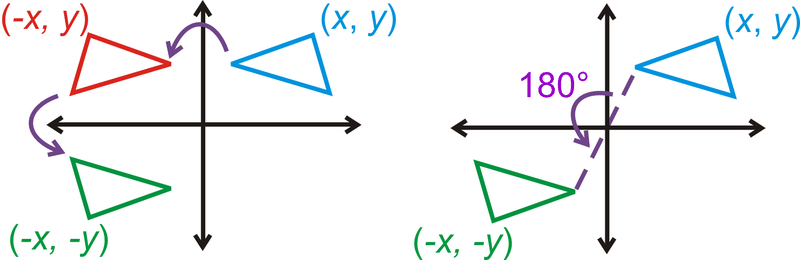
    F-D_729A80EABE 6 ФА0Ф48 ДБ1Б33А4Б3А4Б31855Е31ФБ54291 ЦББД 61CE07085+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Композиція з двох відображень над лініями, які перетинаються на\(x^{\circ}\) те саме, що і обертання\(2x^{\circ}\). Центр обертання - точка перетину двох ліній відображення (Теорема про відбиття над перетинаються лініями).

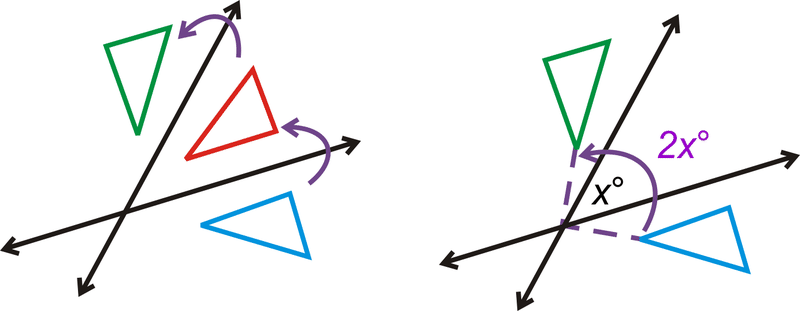
    F-д_8909А91 ДБ3С62ДА9ДАФД 2 АБФ 5939А79Д90ФК 6672300E54805D5EB02+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Що робити, якщо вам дали координати чотирикутника, і вас попросили відобразити чотирикутник, а потім перевести його? Якими будуть його нові координати?

    Приклад\(\PageIndex{1}\)

    Відображати\(\Delta ABC\) над\(y\) -віссю, а потім перевести зображення на 8 одиниць вниз.

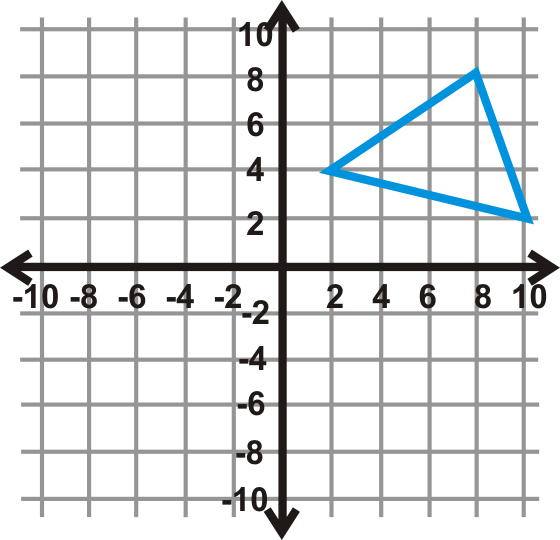
    Ф-д_ЕКА 88ДА091Ф6Ф7360393Ф28Д7 ЕЦ5Д586089Ф189Б 6ДФ34ФКК4Б26А76+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Зелене зображення зліва є остаточною відповіддю.

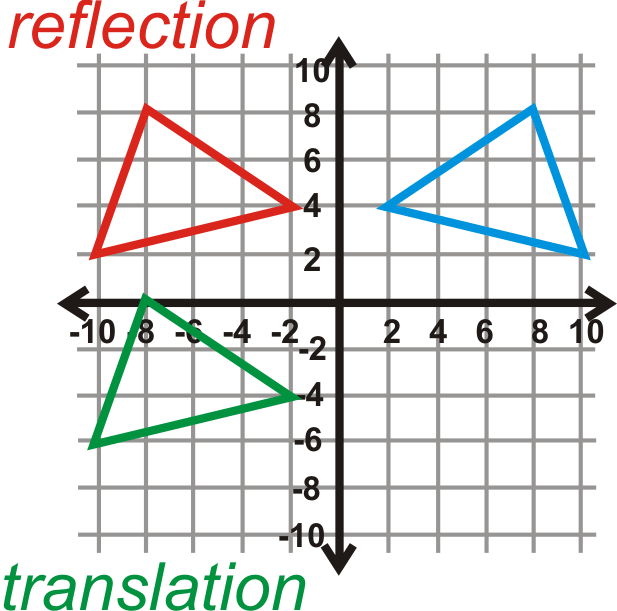
    F-д_48С8 АА 375Д5811Ф149Б15С4Ф7Б4Е5Ф27С КАС 41Б6Д04Е067Ф935211+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    \(\begin{aligned} A(8,8)&\rightarrow A′′(−8,0) \\ B(2,4)&\rightarrow B′′(−2,−4) \\ C(10,2)&\rightarrow C′′(−10,−6) \end{aligned}\)

    Приклад\(\PageIndex{2}\)

    Напишіть єдине правило для\(\Delta ABC\) to\(\Delta A′′B′′C′′\) з Прикладу 1.

    Рішення

    Дивлячись на координати\(A\) to\(A′′\),\(x\) −value є протилежним знаком, а\(y\) −value -\(y−8\). Тому правило було б\((x,y)\rightarrow (−x,y−8)\).

    Приклад\(\PageIndex{3}\)

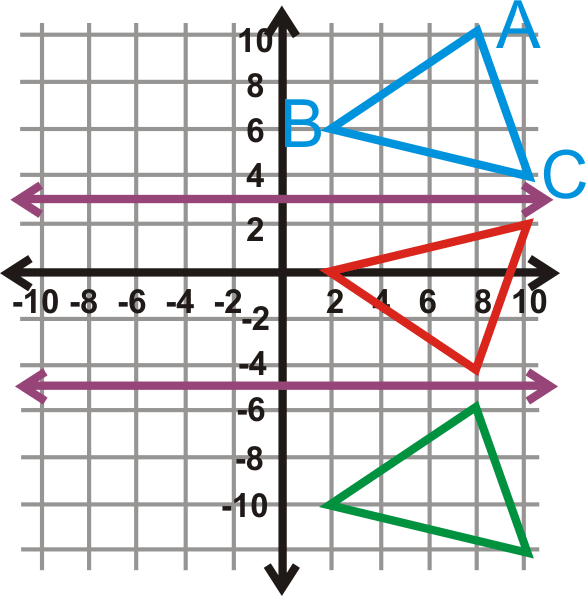
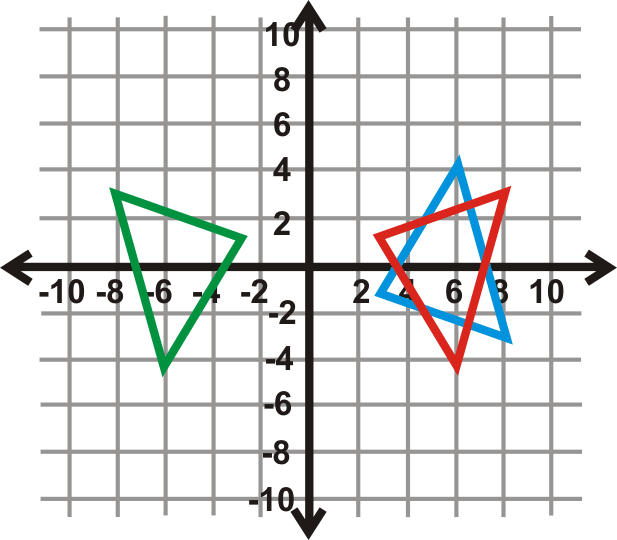
    \(\Delta ABC\)Відображати,\(y=3\) а потім відобразити зображення\(y=−5\).

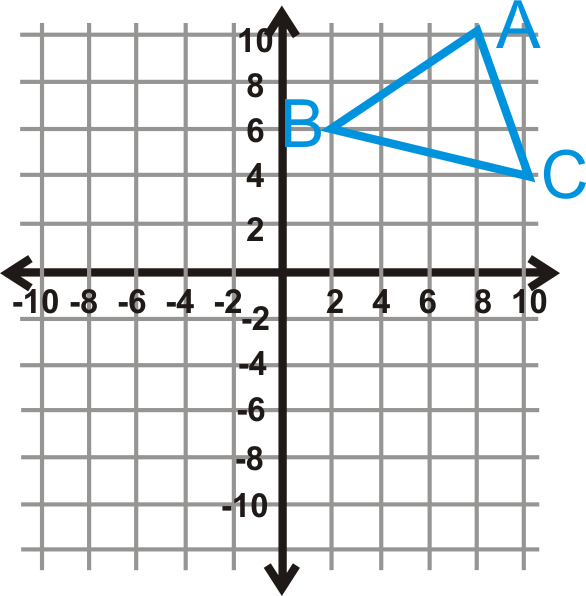
    F-D_A18A7 Б936544А6А3Б9Ф0Д8186ДФД6Д 4Б010Б974309457С39+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Рішення

    Порядок має значення, тому ви б\(y=3\) спочатку подумали (червоний трикутник), а потім відобразити його\(y=−5\) (зелений трикутник).

    Ф-д_5БК 0А6ФА71Ф52341А41А41А6369 СД7А6ДД6А099Б37АААА1Ф3А89Ф21Д+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)

    Приклад\(\PageIndex{4}\)

    Квадрат відбивається над двома лініями, які перетинаються під\(79^{\circ}\) кутом. Яка трансформація буде такою ж, як?

    Рішення

    З теореми про відображення над перетинаються лініями, це те саме, що обертання\(2\cdot 79^{\circ}\) =178^ {\ circ}\).

    Приклад\(\PageIndex{5}\)

    \(\Delta DEF\)має вершини\(D(3,−1)\)\(E(8,−3)\), і\(F(6,4)\). \(\Delta DEF\)Роздумуйте знову\(x=−5\) і потім\(x=1\). Визначте, в якому перекладі це подвійне відображення було б таким же, як.

    Рішення

    З теореми про роздуми над паралельними лініями ми знаємо, що це подвійне відображення буде таким самим, як одиночний переклад\(2(1−(−5))\) або одиниць 12.

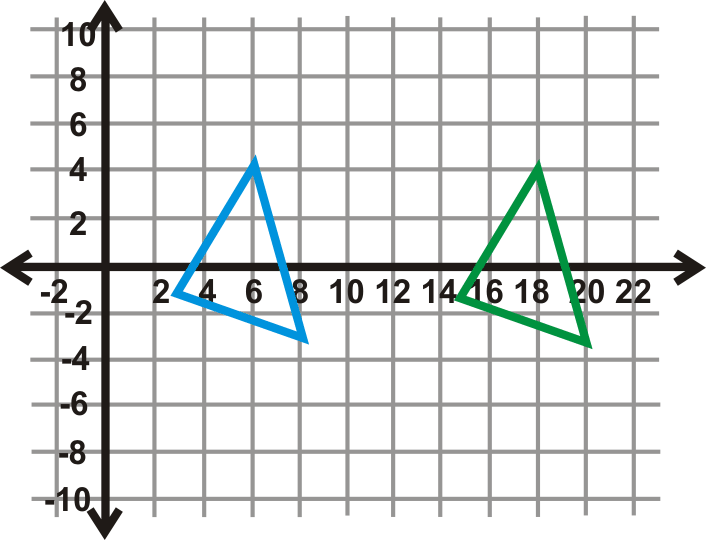
    F-д_822Б22824713С88344Б6774 Б3С1АС699БД9Д32С9БД6Б000С180221+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)

    Приклад\(\PageIndex{6}\)

    \(\Delta DEF\)Відображати з питання 2 над\(x\) -вісь, а потім\(y\) -вісь. Знайдіть координати\(\Delta D′′E′′F′′\) і одне перетворення цього подвійного відображення таке ж, як.

    Рішення

    \(\Delta D′′E′′F′′\)зелений трикутник на графіку зліва. Якщо порівняти координати з ним\(\Delta DEF\), ми маємо:

    Ф-д_7349732563А450 Е080Е9А30А3ФД01Б6АЕ0Ф3Ф5Ф77Д936К1Ф24Ф82С4+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)

    \(\begin{aligned}D(3,−1)&\rightarrow D′′(−3,1) \\ E(8,−3)&\rightarrow E′′(−8,3) \\ F(6,4)&\rightarrow F′′(−6,−4)\end{aligned}\)

    Рецензія

    1. Поясніть, чому склад двох і більше ізометрій також повинен бути ізометрією.
    2. Яке одне перетворення таке ж, як відображення над двома паралельними лініями?
    3. Яке одне перетворення таке ж, як відображення над двома перетинаються лініями?

    Використовуйте графік квадрата зліва, щоб відповісти на питання 4-6.

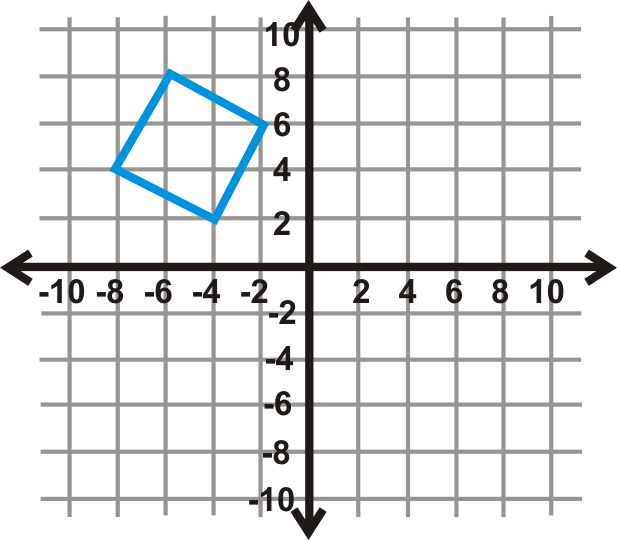
    F-д_ФА 1БД 9667422810C2AE3265BC де 299ЕС39 ЕБ995ЕБ8ДЕ18А9Ф447Б7Е7+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{11}\)
    1. Виконайте відображення ковзання над\(x\) -віссю і вправо 6 одиниць. Напишіть нові координати.
    2. Яке правило для цього відображення ковзання?
    3. Яке відображення ковзання поверне зображення назад до попереднього зображення?

    Використовуйте графік квадрата зліва, щоб відповісти на питання 7-9.

    F-д_ФА 1БД 9667422810C2AE3265BC де 299ЕС39 ЕБ995ЕБ8ДЕ18А9Ф447Б7Е7+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{12}\)
    1. Виконайте відбиття ковзання вправо на 6 одиниць, потім над\(x\) -віссю. Напишіть нові координати.
    2. Яке правило для цього відображення ковзання?
    3. Чи відрізняється правило в #8, ніж правило в #5? Чому чи чому ні?

    Використовуйте графік трикутника зліва, щоб відповісти на 10-12 питань.

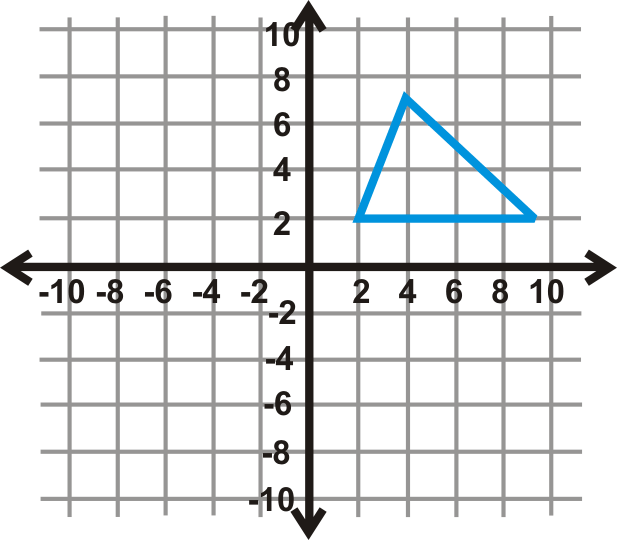
    Ф-Д_Б9БД БББ 04 КД3С1СД 335Д605А35 ББ9105А11КС9ФФ 128Д22081626КС84+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{13}\)
    1. Виконайте відображення ковзання по\(y\) осі -і вниз на 5 одиниць. Напишіть нові координати.
    2. Яке правило для цього відображення ковзання?
    3. Яке відображення ковзання поверне зображення назад до попереднього зображення?

    Використовуйте графік трикутника зліва, щоб відповісти на питання 13-15.

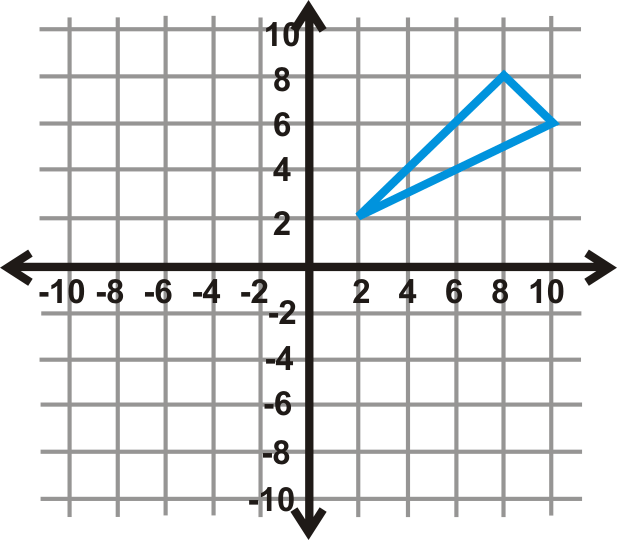
    F-д_7Б40Е7111СА842А0695 ДД1Б5037СА305Е486А1ДФ5ДФ 6ФА1А595638+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{14}\)
    1. Відображати попереднє зображення над\(y=−1\) подальшим\(y=−7\). Намалюйте новий трикутник.
    2. Яка трансформація є таким же подвійним відображенням?
    3. Напишіть правило.

    Використовуйте графік трикутника зліва, щоб відповісти на питання 16-18.

    F-д_7Б40Е7111СА842А0695 ДД1Б5037СА305Е486А1ДФ5ДФ 6ФА1А595638+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{15}\)
    1. Відображати попереднє зображення над\(y=−7\) подальшим\(y=−1\). Намалюйте новий трикутник.
    2. Яка трансформація є таким же подвійним відображенням?
    3. Напишіть правило.
    4. Чим відрізняються кінцеві трикутники в #13 і #16?

    Використовуйте трапецію на графіку зліва, щоб відповісти на питання 20-22.

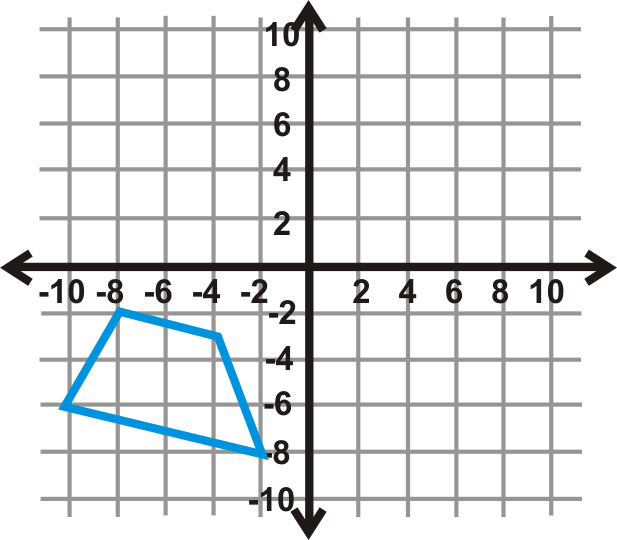
    F-D_38Е 85С61570399E9672 FCFDF 1d75579a9a94дфа5874Б11683E33C93B2B+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{16}\)
    1. Відобразіть попереднє зображення над\(x\) -віссю, а потім\(y\) -вісь. Намалюйте нову трапецію.
    2. Тепер почніть спочатку. Відобразіть трапецію над\(y\) -віссю, потім\(x\) -вісь. Намалюйте цю трапецію.
    3. Чи відрізняються кінцеві трапеції від #20 та #21? Чому ви думаєте, що це так?

    Дайте відповідь на питання нижче. Будьте настільки конкретними, наскільки можете.

    1. Дві паралельні лінії знаходяться на відстані 7 одиниць один від одного. Якщо ви відобразите фігуру над тим, як далеко один від одного з попереднім зображенням і остаточним зображенням бути?
    2. Після подвійного відображення над паралельними лініями попереднє зображення та його зображення знаходяться на відстані 28 одиниць один від одного. Наскільки далеко один від одного розташовані паралельні лінії?
    3. Дві лінії перетинаються під\(165^{\circ}\) кутом. Якщо фігура відбивається над обома лініями, наскільки далеко один від одного буде попереднє зображення та зображення?
    4. Що таке центр обертання для #25?
    5. Дві лінії перетинаються під\(83^{\circ}\) кутом. Якщо фігура відбивається над обома лініями, наскільки далеко один від одного буде попереднє зображення та зображення?
    6. Передзображення та його образ є\(244^{\circ}\) відокремленими. Якщо передзображення відбивалося над двома пересічними лініями, під яким кутом вони перетиналися?
    7. Передзображення та його образ є\(98^{\circ}\) відокремленими. Якщо передзображення відбивалося над двома пересічними лініями, під яким кутом вони перетиналися?
    8. Після подвійного відображення над паралельними лініями попередній образ і його зображення знаходяться на відстані 62 одиниць один від одного. Наскільки далеко один від одного розташовані паралельні лінії?

    Огляд (Відповіді)

    Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 12.6.

    Лексика

    Термін Визначення
    склад (перетворень) Коли на фігурі виконується не одне перетворення.
    Обертання Обертання - це перетворення, яке перетворює фігуру на координатній площині на певну кількість градусів навколо заданої точки без зміни форми або розміру фігури.
    Відображення Відбиття - це перетворення, яке перевертає фігуру на координатній площині через задану лінію без зміни форми або розміру фігури.
    Відбиття ковзання Відображення з подальшим перекладом, де лінія відображення паралельна напрямку перекладу, називається відображенням ковзання або прогулянкою.
    Композитна трансформація Композитне перетворення, також відоме як композиція перетворення, являє собою серію множинних перетворень, що виконуються одна за одною.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи складання трансформацій - основні

    Види діяльності: Склад трансформацій Дискусійні питання

    Навчальні посібники: Навчальний посібник зі складу трансформацій

    Практика: Композитні перетворення