8.3: Симетрія відображення

Last updated

Oct 27, 2022
Save as PDF
- 8.2: Лінії симетрії
- 8.4: Симетрія обертання

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Властивість фігури з однією або декількома лініями симетрії.

Лінія симетрії - це лінія, яка проходить через фігуру таким чином, що вона розділяє фігуру на дві конгруентні половини таким чином, що якщо одна половина була складена поперек лінії симетрії, вона приземлилася б прямо поверх іншої половини.

F-D_E32568C4D0C3 ЕАБ 68А 5А2БА5С7А5С7294Б60917БАФ 1ФБ 96БФ2FF3+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Відображення симетрії присутній, коли фігура має одну або кілька ліній симетрії. Ці фігури мають симетрію відображення:

F-д_4170355c1f9a7721cd63А326407Б821552CA688D36885201c06C340+зображення_крихіткий+зображення_крихіткий_png — Малюнок $\PageIndex{2}$

Ці фігури не мають симетрії відображення:

F-D_B90FC9 АФБ9ДБ9ДБ9ДБ 1976 АФ 5Ф9Ф09Б67А561Д1Б84083Б7422 ЕББ1+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Що робити, якщо у вас була шестикутна зірка, ви намалювали лінію вниз, а потім склали її вздовж цієї лінії? Якби дві сторони зірки вишикувалися, що б це означало про лінію?

Приклад $\PageIndex{1}$

Знайдіть усі лінії симетрії для фігури нижче.

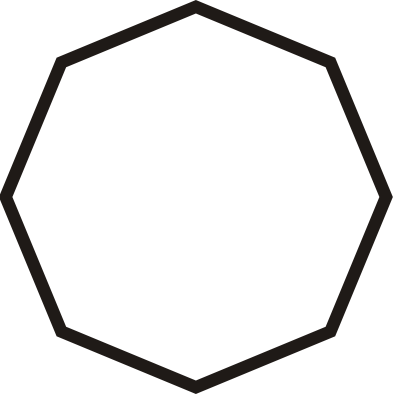
F-D_26888E2B4 АЦБ 88d76cd15e670cd68b90B28A3A693022FD4E1985+зображення_крихіткий+зображення_крихіткий_крошечкою.PNG — Малюнок $\PageIndex{4}$

Рішення

Проведіть лінії по фігурі так, щоб лінії ідеально розрізали фігуру навпіл. Ця цифра має вісім ліній симетрії.

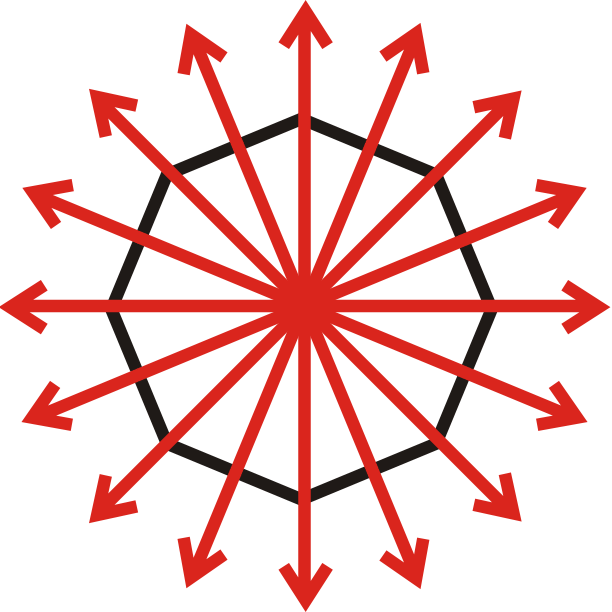
F-д_афф 530794 FBE87923690D24E53E0595C48E960B3163 ФАБ5825ЕДДД 61+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{5}$

Приклад $\PageIndex{2}$

Знайдіть усі лінії симетрії для фігури нижче.

Ф-д_5Е5Е843Е58Ф68А0А4СБ99БА 2285А874Д0Ф5Ф5Ф58К1А014А742де8+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{6}$

Рішення

Не можна проводити лінії через фігуру так, щоб лінії ідеально розрізали фігуру навпіл, тому ця фігура не має ліній симетрії.

Приклад $\PageIndex{3}$

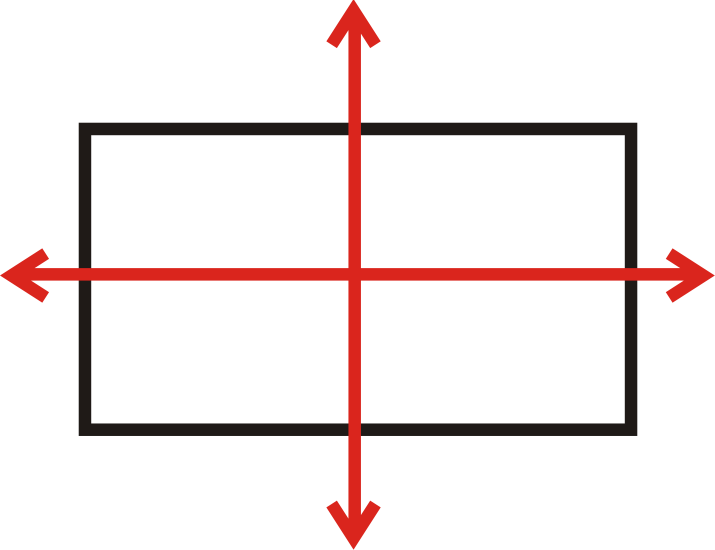
Знайдіть усі лінії симетрії для фігури нижче.

F-д_59Б8Д2КС0А6 ЕЕ2 ЦЕЕ8А60Ф9935ДФ1Д07С7Б14433Д531147318C8E685+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{7}$

Рішення

Ця фігура має дві лінії симетрії.

F-D_B9A Додати 8749829 ББ1Е82Д33704C1450А9С7Б5 Бад 33Б87171C20+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{8}$

Приклад $\PageIndex{4}$

Чи має малюнок нижче симетрію відображення?

F-д_35С78А6 АБ 9С4155А1А52А64805ФЦ17Ф5 АБФФ 7CDEB9A541D1375EA6A+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{9}$

Рішення

Так, ця фігура має симетрію відображення.

F-D_DC 47C51022FFA48C BAA446358D4927B3E6588333577 ADC 55C6057163+зображення_крихіткий+зображення_крихіткий_png — Малюнок $\PageIndex{10}$

Приклад $\PageIndex{5}$

Чи має малюнок нижче симетрію відображення?

F-д_0е4ф 49д 553E4A55c7 фаф 26cd21526ce1d209e421a4517a8926800D48+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{11}$

Рішення

Так, ця фігура має симетрію відображення.

F-D_F53DE1 АБ3Ф8АЦ907СА1797Б6ФД CF8780C5D9892AFC9CD37C72E3F738+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{12}$

Рецензія

Визначте, чи є кожне твердження істинним чи помилковим.

Всі правильні трикутники мають симетрію ліній.
Всі рівнобедрені трикутники мають симетрію ліній.
Кожен прямокутник має симетрію ліній.
Кожен прямокутник має рівно дві лінії симетрії.
Кожен паралелограм має симетрію лінії.
Кожен квадрат має рівно дві лінії симетрії.
Кожен правильний багатокутник має три лінії симетрії.
Кожен сектор кола має лінію симетрії.

Намалюйте наступні фігури.

Чотирикутник, який має дві пари конгруентних сторін і рівно одну лінію симетрії.
Фігура з нескінченною кількістю ліній симетрії.

Знайдіть всі лінії симетрії для букв нижче.

Малюнок $\PageIndex{13}$
Малюнок $\PageIndex{14}$
Малюнок $\PageIndex{15}$
Малюнок $\PageIndex{16}$
Малюнок $\PageIndex{17}$

Визначте, чи мають наведені нижче слова симетрію відображення.

ОГАЙО
КОСИТИ
WOW
УДАР
стручок

Проведіть кожну фігуру, а потім проведіть у всіх лініях симетрії.

Малюнок $\PageIndex{18}$
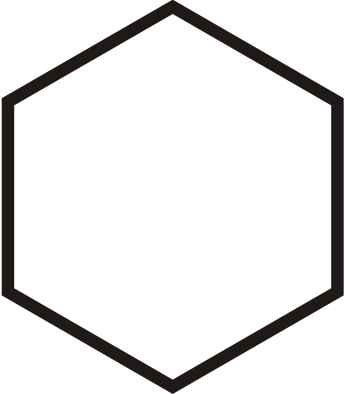
Малюнок $\PageIndex{19}$
Малюнок $\PageIndex{20}$

Визначте, чи мають наведені нижче цифри симетрію відображення. Визначте всі лінії симетрії.

Малюнок $\PageIndex{13}$
Малюнок $\PageIndex{13}$
Малюнок $\PageIndex{13}$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 12.1.

Лексика

Термін	Визначення
Лінія симетрії	Лінія симетрії - це лінія, яку можна провести, щоб розділити фігуру на рівні половини.
Конгруентний	Конгруентні фігури ідентичні за розміром, формою і мірою.
Рівнобедрений трикутник	Рівнобедрений трикутник - це трикутник, у якого рівно дві сторони мають однакову довжину.
Симетрія ліній	Фігура має симетрію лінії або симетрію відображення, коли її можна розділити на рівні половини, які збігаються.
симетрія відображення	Фігура має симетрію відображення, якщо вона може бути відображена через лінію і виглядати точно так само, як і до відображення.
Симетрія	Фігура має симетрію, якщо її можна перетворити і при цьому виглядати однаково.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи симетрії відображення - основні

Види діяльності: Відображення Симетрія Дискусії Питання

Навчальні посібники: Посібник з вивчення симетрії та тесселяції

Практика: Відображення симетрії