8.9: Позначення перекладу
- Page ID
- 54886
Графічне введення в переклади зображень. Навчіться використовувати нотації для опису правил відображення та зображень графіків, заданих попереднім зображенням та перекладом
Правила перекладу
Джек описує переклад як точку, що рухається від\(J(−2, 6)\) до\(J′(4,9)\). Напишіть правило відображення, щоб описати цей переклад для Джека.
У геометрії трансформація - це операція, яка переміщує, перевертає або змінює фігуру (називається попереднім зображенням) для створення нової форми (званої зображенням). Переклад - це тип перетворення, який переміщує кожну точку фігури на однакову відстань в одному напрямку. Переклади часто називають слайдами. Ви можете описати переклад, використовуючи такі слова, як «переміщено вгору 3 і більше 5 ліворуч» або з позначеннями. Існує два типи позначень, які потрібно знати.
- Одне позначення виглядає так\(T_{(3, 5)}\). Це позначення говорить вам додати 3 до\(x\) значень і додати 5 до\(y\) значень.
- Друге позначення - правило відображення виду\((x,y) \rightarrow (x−7, y+5)\). Це позначення говорить вам, що\(y\) координати\(x\) і перекладені на\(x−7\) і\(y+5\).
Позначення правила відображення є найбільш поширеним.
Інтерактивний елемент
Давайте напишемо правило відображення для кожного з наступних перекладів:
- Сара описує переклад як точку,\(P\) що рухається від\(P(−2,2)\) до\(P′(1,−1)\).
Загалом,\(P(x, y) \rightarrow P′(x+a, y+b)\).
У цьому випадку,\(P(−2, 2) \rightarrow P′(−2+a, 2+b)\) або\(P(−2, 2) \rightarrow P′(1, −1)\)
Тому:
\ (\ begin {масив} {rr}
-2+a=1 &\ текст {і}\ quad 2+b = -1\\
a=3 &\ quad b = -3
\ end {масив}\)
Правило таке:\((x,y) \rightarrow (x+3, y−3)\)
- Mikah описує переклад як точку D на діаграмі, що рухається від\(D(1, −5)\) до\(D′(−3,1)\).
Загалом,\(P(x,y) \rightarrow P′(x+a, y+b)\).
У цьому випадку,\(D(1,−5) \rightarrow D′(1+a,−5+b)\) або\(D(1,−5) \rightarrow D′(−3,1)\)
Тому:
\ (\ begin {масив} {rrr}
1+a=-3 &\ текст {і} & -5+b=1\
a=4 & & b=6
\ end {масив}\)
Правило таке:\((x,y) \rightarrow (x−4, y+6)\)
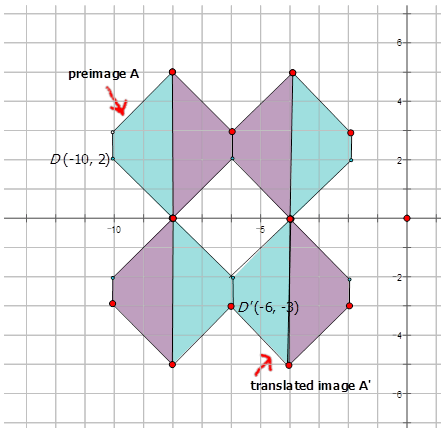
- Переклад попереднього зображення на\(A\) перекладене зображення на\(J\) діаграмі нижче:
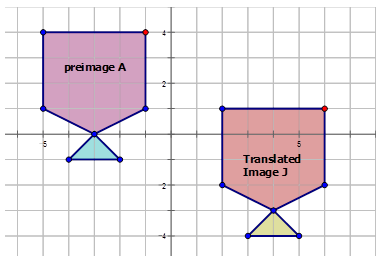
Спочатку виберіть точку на діаграмі, щоб побачити, як вона перекладається.
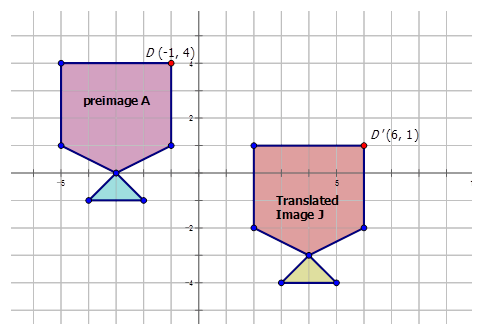
\(D:(−1,4) D′:(6,1)\)
\(D(x,y) \rightarrow D′(x+a,y+b)\)
Отже:\(D(−1,4) \rightarrow D′(−1+a,4+b)\) або\(D(−1,4) \rightarrow D′(6,1)\)
Тому:
\ (\ begin {масив} {rrr}
-1+a=6 &\ текст {і} & 4+b=1\
a=7 & b=-3
\ end {масив}\)
Правило таке:\((x,y) \rightarrow (x+7,y−3)\)
Приклад\(\PageIndex{1}\)
Раніше вам сказали, що Джек описав переклад як точку, що\(J\) рухається від\(J(−2,6)\) до\(J′(4,9)\). Що таке правило відображення, яке описує цей переклад?
Рішення
\((x,y) \rightarrow (x+6, y+3)\)
Приклад\(\PageIndex{2}\)
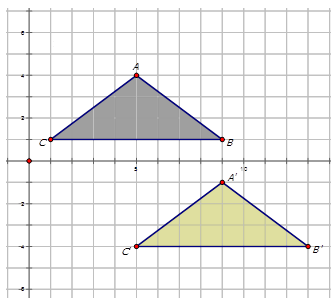
Напишіть правило відображення, яке представляє переклад червоного трикутника до перекладеного зеленого трикутника на діаграмі нижче.
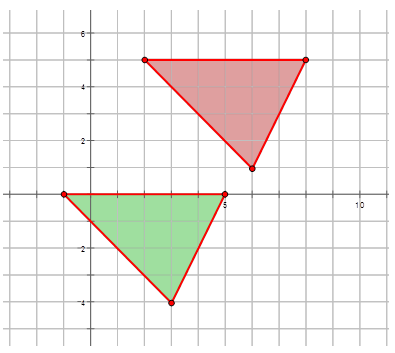
Рішення
\((x, y) \rightarrow (x−3, y−5)\)
Приклад\(\PageIndex{3}\)
Наступний візерунок є частиною шпалер, знайдених у вестибюлі готелю. Напишіть правило відображення, яке представляє переклад однієї синьої трапеції на перекладену синю трапецію, показану на діаграмі нижче.
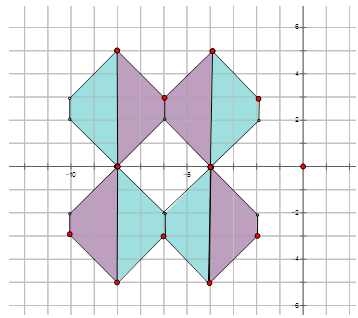
Рішення
Якщо придивитися до наведеної нижче схеми, то там дві пари трапецій, які є перекладами один одного. Тому ви можете вибрати одну синю трапецію, яка є перекладом іншої, і вибрати точку, щоб дізнатися, наскільки фігура перемістилася, щоб дістатися до перекладеного положення.
Для цих двох трапецій:\((x,y) \rightarrow (x+4, y−5)\)
Рецензія
Напишіть правило відображення, щоб описати рух точок у кожному з наведених нижче перекладів.
- \(S(1,5) \rightarrow S′(2,7)\)
- \(W(−5,−1) \rightarrow W′(−3,1)\)
- \(Q(2,−5) \rightarrow Q′(−6,3)\)
- \(M(4,3) \rightarrow M′(−2,9)\)
- \(B(−4,−2) \rightarrow B′(2,−2)\)
- \(A(2,4) \rightarrow A′(2,6)\)
- \(C(−5,−3) \rightarrow C′(−3,4)\)
- \(D(4,−1) \rightarrow D′(−4,2)\)
- \(Z(7,2) \rightarrow Z′(−3,6)\)
- \(L(−3,−2) \rightarrow L′(4,−1)\)
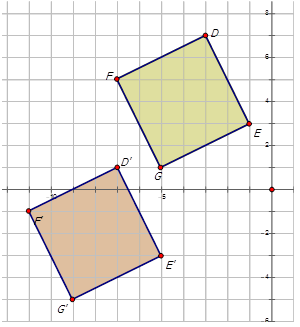
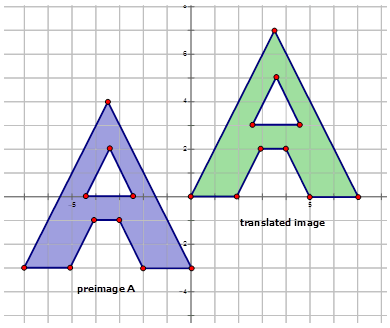
Напишіть правило відображення, яке представляє переклад попереднього зображення на зображення для кожної діаграми нижче.
-
Малюнок\(\PageIndex{6}\) -
Малюнок\(\PageIndex{7}\) -
Малюнок\(\PageIndex{8}\) -
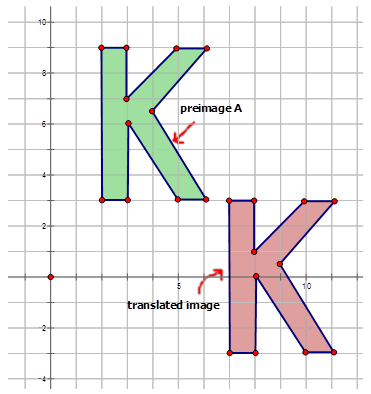
Малюнок\(\PageIndex{9}\) -
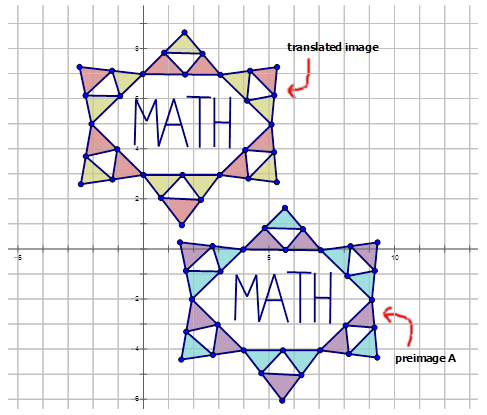
Малюнок\(\PageIndex{10}\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.3.
Додаткові ресурси
Інтерактивний елемент
Відео: Квадранти координатної площини
Практика: Позначення перекладу