8.16: Відображаючі цифри
- Page ID
- 54896
Переміщення фігур на координатній площині за допомогою візерунків.
Переклади, обертання та роздуми
Тайлер фотографує предмет і його відображення. Він розміщує координатну площину над малюнком. Координатна площина розташована так, що\(x\) вісь −відокремлює зображення від відбиття. Потім він робить сітку відповідно до ключових особливостей малюнка, так що точка в\((2, 0)\) відбивається в точці\((-2, 0)\). Якщо вихідні координати зображення є\((3, 0)\),\((4, 6)\) і\((5, 1)\), які координати відображення?

У цій концепції ви дізнаєтеся, як знайти координати для перекладів, обертань і роздумів.
Пошук координат для перекладів, обертань та роздумів
Коли ви виконуєте переклади, ви ковзаєте фігуру вліво або вправо, вгору або вниз. Це означає, що на координатній площині координати вершин фігури будуть змінюватися.
Щоб скласти графік перекладу, виконайте однакові зміни для кожної точки.
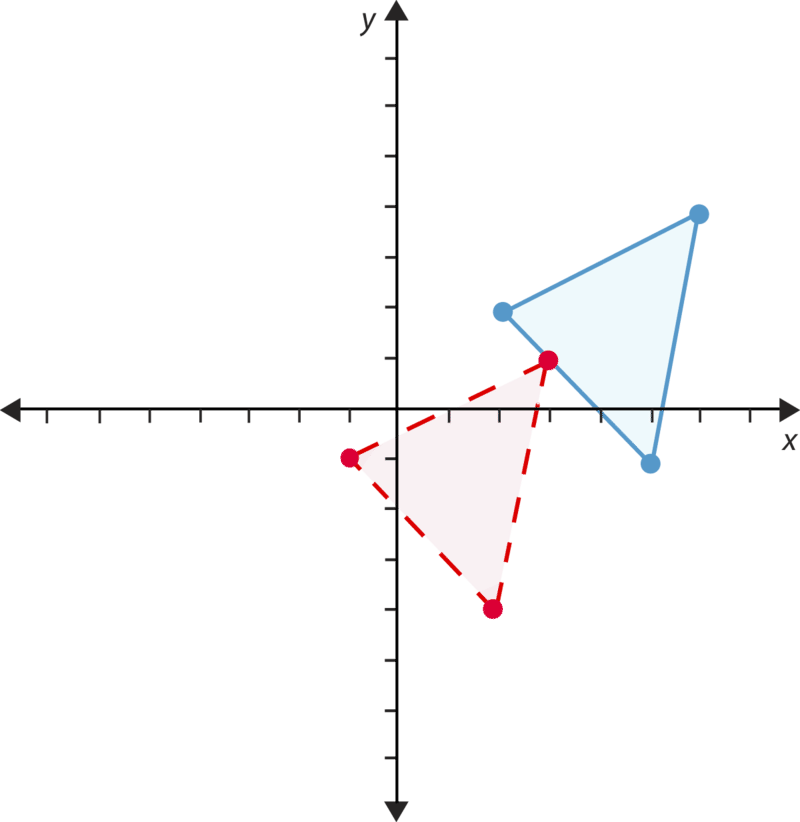
Ви можете ідентифікувати відображення за змінами його координат. У відображенні фігура перевертається поперек лінії, щоб зробити дзеркальне відображення себе. Погляньте на відображення нижче.
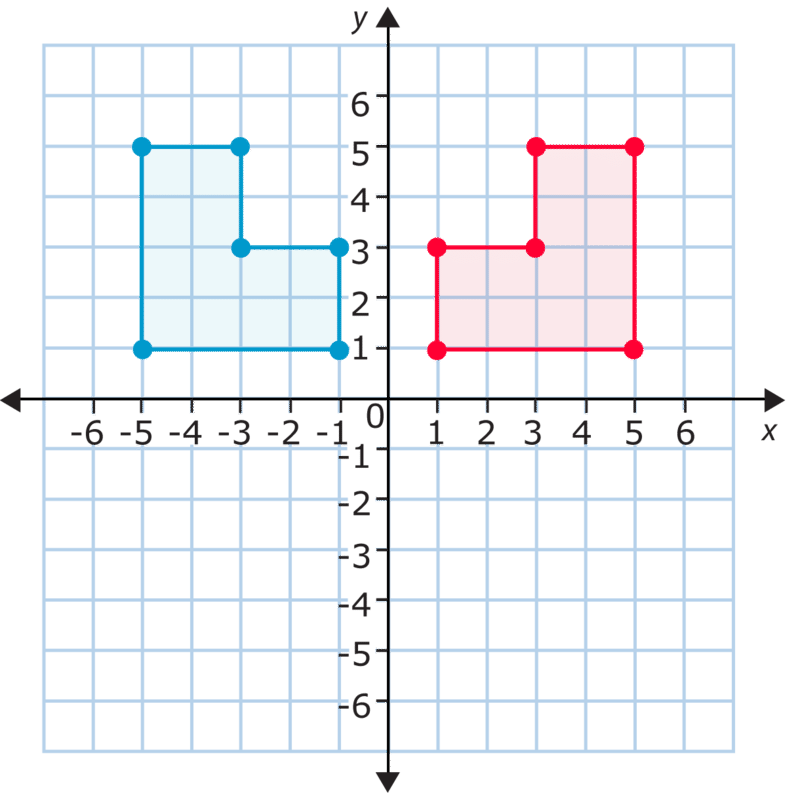
Цифри зазвичай відображаються по\(y\) осі\(x\) − або -. При цьому фігура відбивається поперек\(y\) -осі. Якщо ви порівнюєте цифри у першому прикладі вершини за вершиною, ви побачите, що\(x\) −coordinates змінюються, але\(y\) −coordinates залишаються незмінними. Це пов'язано з тим, що відображення відбувається зліва направо через\(y\) -вісь. Якщо ви відбиваєте по\(x\) осі\(y\) −координати, −coordinates змінюються, а\(x\) −coordinates залишаються незмінними. Погляньте на цей приклад.
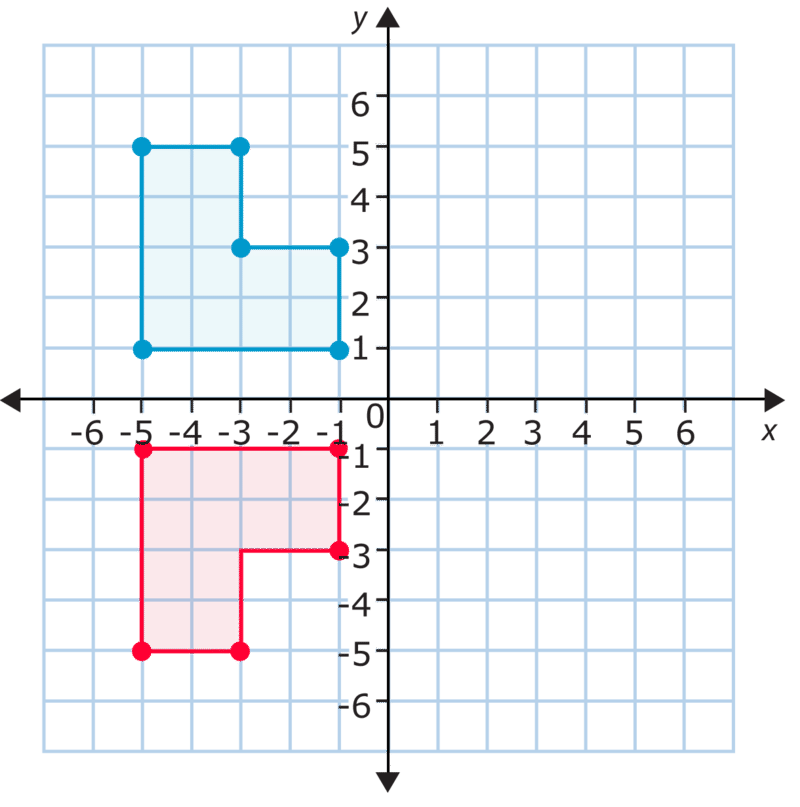
На малюнку вище вказані координати лівої верхньої вершини вихідної фігури\((-5, 5)\). Після того, як ви відобразите його по\(x\) осі −−, координати відповідної вершини будуть\((-5, -5)\). Як щодо нижньої правої вершини? Він починається в\((-1, 1)\), і після фліп він знаходиться на\((-1, -1)\). Як ви можете бачити,\(x\) −coordinates залишаються незмінними, поки параметри\(y\) −coordinates змінюються. Фактично, всі\(y\) −координати стають протилежними цілими числами початкових\(y\) −координат. Це означає, що це вертикальне (вгору/вниз) відображення або відображення над\(x\) віссю −.
У горизонтальному (ліво/правому) відображенні або відображенні над\(y\) віссю\(x\) -координати стануть цілими протилежностями. Давайте розглянемо приклад.
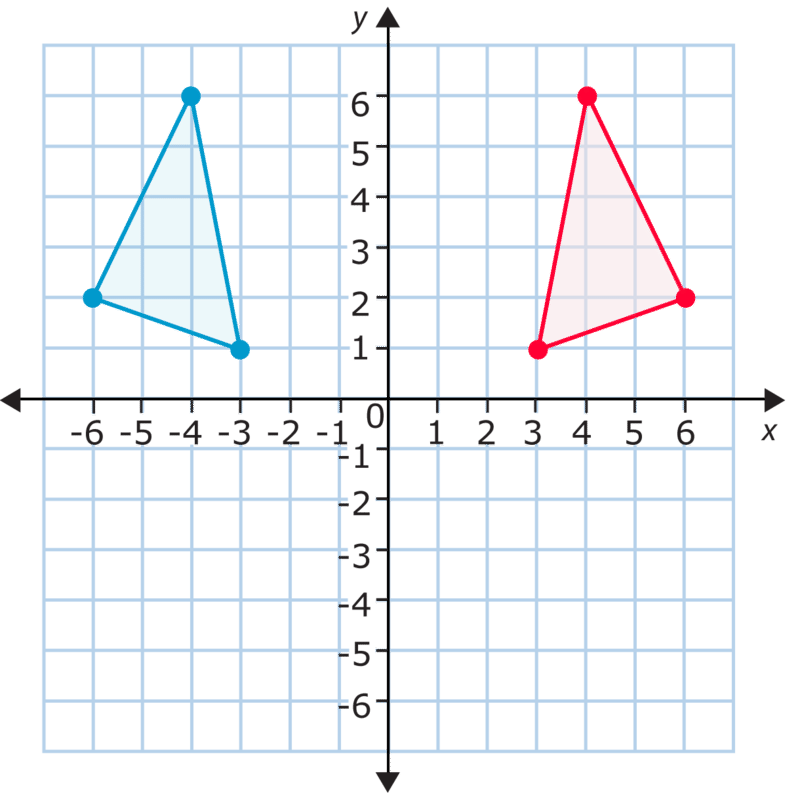
Це відображення поперек\(y\) -осі. Порівняйте пункти. Зауважте, що\(y\) −координати залишаються незмінними. \(x\)−coordines стають цілими протилежностями початкових\(x\) −координат. Подивіться на верхню точку трикутника, наприклад. Координати початкової точки є\((-4, 6)\), а координати нової точки -\((4, 6)\). \(x\)−coordinate було змінено з -4 на 4.
Ви можете розпізнати відображення за цими змінами\(y\) координат\(x\) − та −. Якщо ви відобразите по\(x\) осі\(y\) −−координати, параметри −coordinates стануть протилежними. Якщо ви відобразите поперек\(y\) -осі,\(x\) −coordinates стане протилежним.
Ви також можете використовувати цю інформацію для графіків відображень. Щоб намалювати відображення, вам потрібно вирішити, чи буде відображатися поперек\(x\) −осі або\(y\) -осі, а потім змінити\(y\) координати\(x\) − або −.
Тепер давайте розглянемо третій вид трансформації: обертання. Обертання - це перетворення, яке повертає фігуру або за годинниковою стрілкою, або проти годинникової стрілки. Малюнок нижче був повернутий. Які його нові координати?
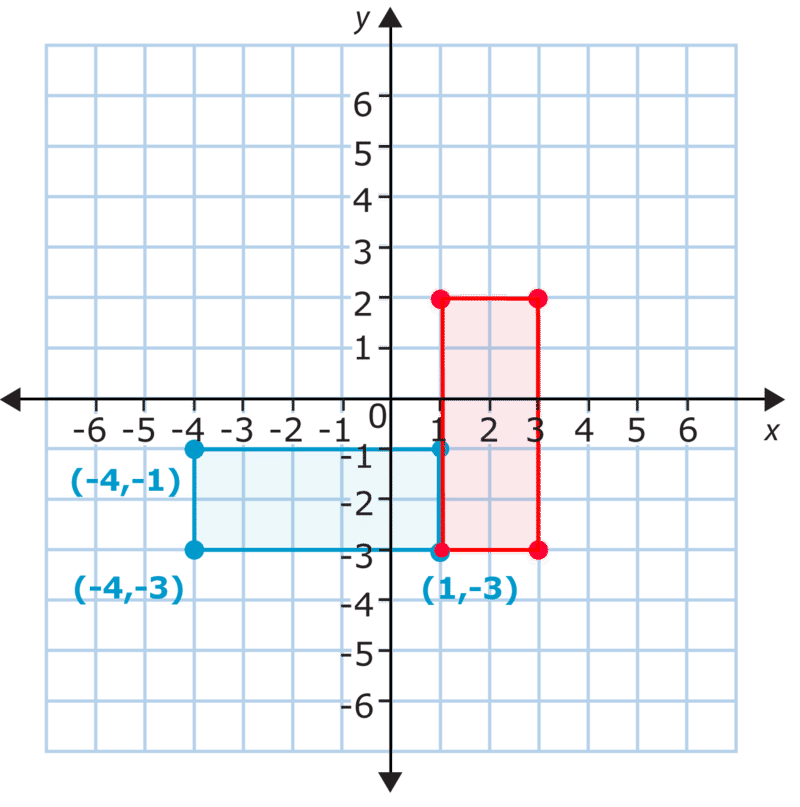
Нові координати вершин прямокутника:\((1, -3)\)\((1, 2)\),\((3, 2)\), і\((3, -3)\). Як ви можете бачити, змінилися як\(y\) координати\(x\) −, так і −. Один з пунктів залишився точно таким же. Це означає, що фігура була повернута навколо цієї точки. Уявіть, що ви поклали палець на цей кут прямокутника і закручували його. Ось що сталося в ротації. Прямокутник повернуто\(90^{\circ}\) за годинниковою стрілкою.
Коли ви графуєте обертання, спочатку потрібно знати, на скільки буде повертатися фігура. Обертаючи прямокутник вгорі, він\(90^{\circ}\) стоїть на кінці. Обертання його\(180^{\circ}\) зробить його знову плоским. Ви також повинні знати, в якій точці ви будете обертати його навколо. Це той момент, який залишається незмінним.
Далі потрібно порахувати, скільки одиниць довжини і ширини становить цифра. Наведена вище цифра тягнеться від 1 по\(x\) осі −4 на\(x\) осі −4. Це всього 5 одиниць вздовж\(x\) осі −. Коли ви обертаєте фігуру\(90^{\circ}\), відстань на\(x\) осі −стає відстанню на\(y\) осі -. Подивіться на прямокутник. Довгі сторони спочатку горизонтальні, але після того, як ви її обертаєте, вони стають вертикальними сторонами. Це означає, що відстань x−5 стане y−відстанню, рівною 5.
Тепер пам'ятайте, що точка\((1, -3)\) залишається незмінною, тому це один кут повернутої фігури. Ви додаєте 5 до\(y\) −coordinate, щоб знайти наступну вершину прямокутника. \(−3+5=2\). Це ставить вершину в (1, 2)\).
Щоб знайти інші точки повернутого прямокутника, потрібно подумати про його ширині. Знайдіть ширину або коротку сторону вихідного прямокутника, підрахувавши одиниці між вершинами вздовж\(y\) -осі. Прямокутник охоплює 2 одиниці на\(y\) -осі. Як ви могли здогадатися, ця\(x\) відстань стає −distance у повернутій фігурі. Іншими словами, ви додаєте 2 до\(x\) −координати точки, яка залишається незмінною. \(1+2=3\), Таким чином, інша вершина прямокутника буде\((3, -3)\). Щоб знайти четверту та останню вершину, додайте 2 до\(x\) −координати іншої впорядкованої пари\((1, 2)\). Це ставить останню вершину на\((3, 2)\).
Запишіть кожен набір координат, щоб показати відображення в\(y\) -осі.
Приклад\(\PageIndex{1}\)
Раніше вам давали проблему про Тайлера і його фотографії.
Якщо вихідні координати зображення є\((3, 0)\),\((4, 6)\) і\((5, 1)\), які координати відображення?
Рішення
По-перше, запам'ятайте, як відображати поперек\(x\) −осі.
Переверніть форму по\(x\) осі −.
Далі запам'ятайте правила.
\(y\)−coordinates зміниться на їхні цілочисельні протилежності.
Потім напишіть нові пункти.
\((3, 0)\),\((4, -6)\),\((5, -1)\)
Відповідь полягає в тому, що координати відображення є\((3, 0)\),\((4, -6)\),\((5, -1)\).
Приклад\(\PageIndex{2}\)
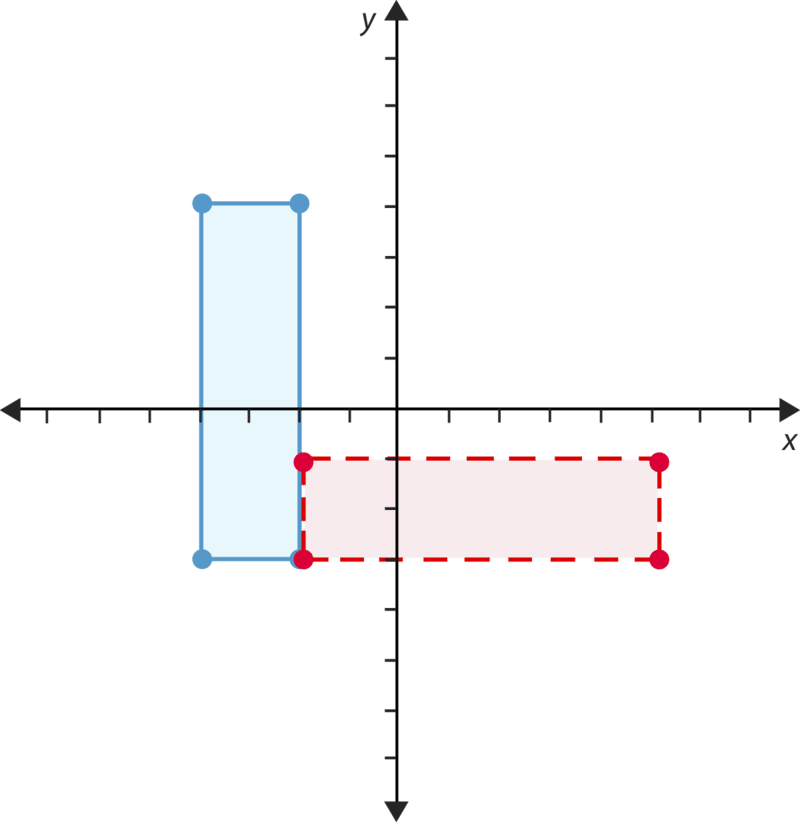
На малюнку нижче відображається поперек\(x\) −осі. Які координати відображення?
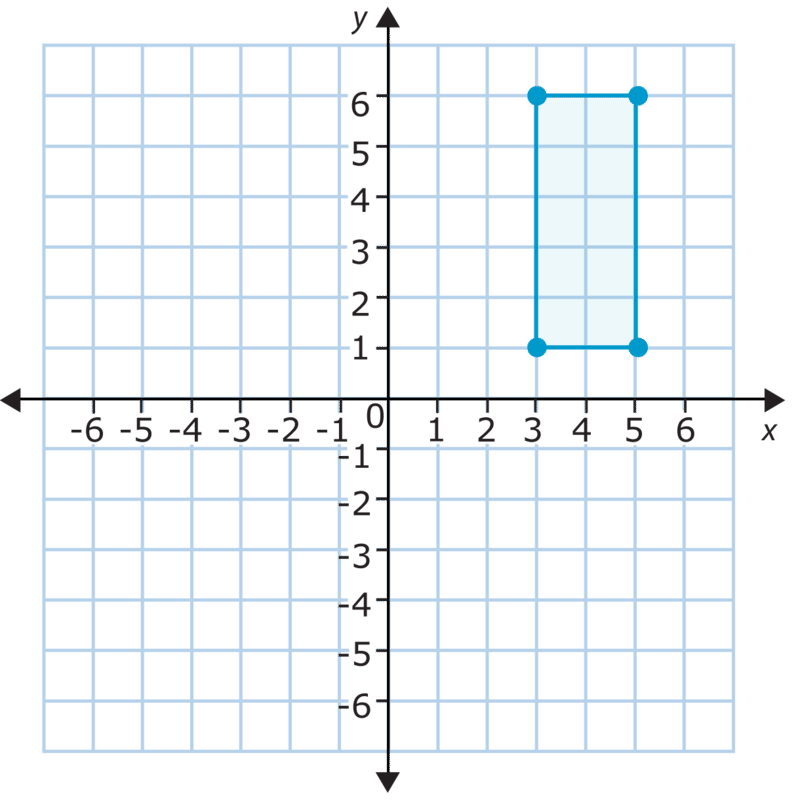
Рішення
По-перше, запам'ятайте, як відображати поперек\(x\) −осі.
Переверніть форму по\(x\) осі −.
Далі запам'ятайте правила.
\(y\)−coordinates зміниться на їхні цілочисельні протилежності.
Потім напишіть нові пункти.
\((3, -6)\),\((3, -1)\),\((5, -6)\),\((5, -1)\)
Відповідь полягає в тому, що координати відображення є\((3, -6)\),\((3, -1)\),\((5, -6)\),\((5, -1)\).
Приклад\(\PageIndex{3}\)
Визначте, чи є зміна результатом перекладу, відображення або обертання.
Після перетворення вершини\((3, 1)\),\((0, 3)\),\((1, 2)\) стають\((3, -1)\),\((0, -3)\),\((1, -2)\).
Рішення
Спочатку подивіться на координати, щоб побачити, які координати змінюються.
\(x\)−coordinates залишаються незмінними, а\(y\) −coordinates змінюються для кожної з точок.
Далі визначаємо тип зміни координат.
Нові\(y\) −координати протилежні початковим координатам.
Потім вкажіть тип трансформації.
Відображення
Відповідь полягає в тому, що зміна є результатом рефлексії.
Приклад\(\PageIndex{4}\)
Визначте, чи є зміна результатом перекладу, відображення або обертання.
Після перетворення вершини\((-3, 6)\),,\((-2, 3)\)\((2, 3)\),\((3, 6)\) стають\((-3, -1)\),\((-2, 8)\),\((2, 8)\),\((3, 11)\).
Рішення
Спочатку подивіться на координати, щоб побачити, які координати змінюються.
\(x\)−coordinates залишаються незмінними, а\(y\) −coordinates змінюються для кожної з точок.
Далі визначаємо тип зміни координат.
Нові\(y\) −координати кожне на 5 більше, ніж початкові координати.
Потім вкажіть тип трансформації.
Переклад
Відповідь полягає в тому, що зміна є результатом перекладу.
Приклад\(\PageIndex{5}\)
Точки\((1, 2)\),,\((3, 7)\)\((3, 4)\),\((5, 6)\) відображаються над\(y\) -віссю. Які нові координати?
Рішення
Спочатку запам'ятайте зміни, які відбуваються з відображенням над\(y\) -віссю.
\(x\)−coordinates стають протилежними, а\(y\) −coordinates залишаються незмінними.
Потім напишіть нові координати.
\((-1, 2)\),\((-3, 7)\),\((-3, 4)\),\((-5, 6)\)
Відповідь полягає в тому, що нові координати є\((-1, 2)\)\((-3, 7)\),,\((-3, 4)\),\((-5, 6)\).
Правда чи брехня. Коли в\(y\) -осі є відображення, обидві координати змінюються на протилежності.
Рецензія
Використовуйте цю цифру, щоб відповісти на кожне питання. Обов'язково запишіть все в позначеннях координат, коли це можливо.
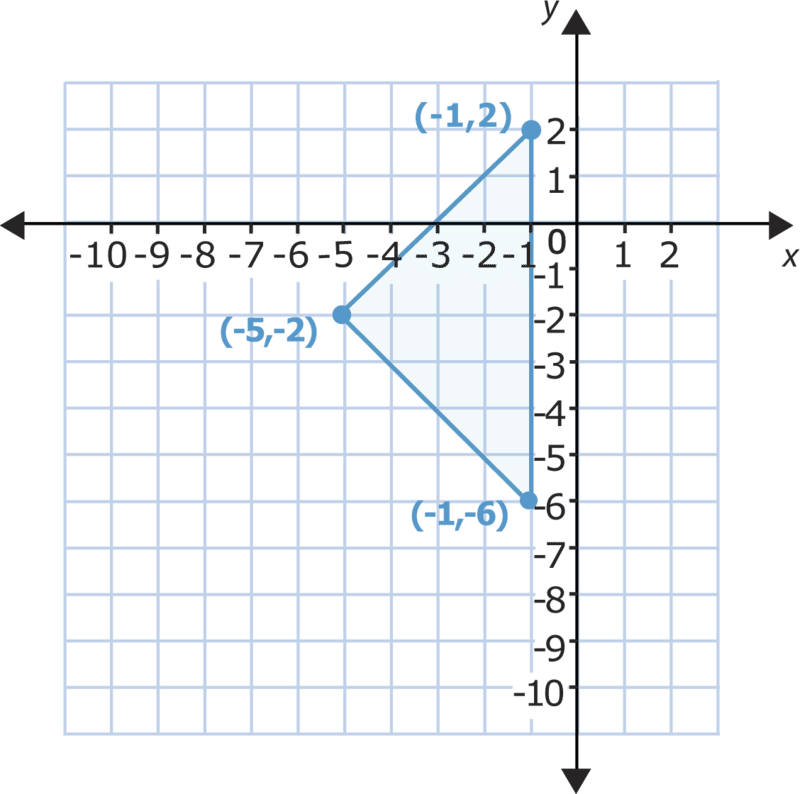
- Переведіть цю цифру на три одиниці вгору.
- Переведіть цю цифру чотири одиниці вправо.
- Переведіть цю цифру на п'ять одиниць вниз.
- Переведіть цю цифру шість одиниць вліво.
- Переведіть цю цифру на одну одиницю вниз і дві одиниці вправо.
- Переведіть цю цифру на дві одиниці вгору і одну одиницю вліво.
- Переведіть цю цифру на три одиниці вгору і одну одиницю вправо.
- Поверніть цю цифру на 180 градусів.
- Поверніть цю цифру на 90 градусів.
- Відобразіть цю цифру над віссю x.
- Відобразіть цю цифру над віссю y.
- Переведіть цю цифру на п'ять одиниць вгору і три одиниці вправо.
- Переведіть цю цифру на шість одиниць вниз і чотири одиниці вліво.
- Правда чи брехня. На малюнку нижче зображено відображення.
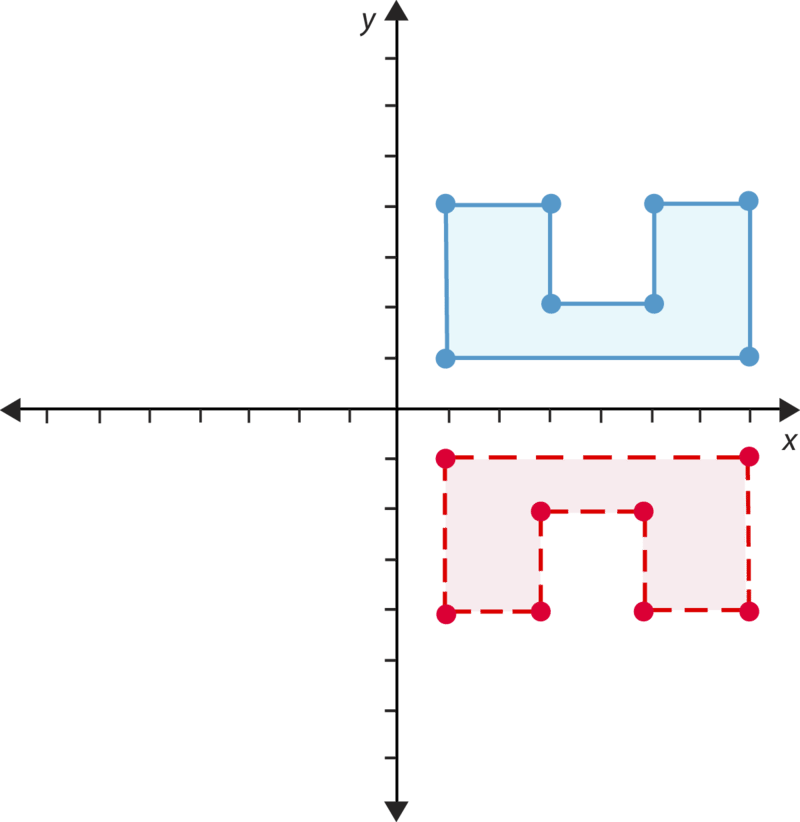
- Правда чи брехня. Ця цифра була повернута\(180^{\circ}\).
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.19.
Ресурси
Лексика
| Термін | Визначення |
|---|---|
| \(x\)−вісь | \(x\)−вісь — це горизонтальна вісь у координатній площині, яка зазвичай представляє значення вхідної або незалежної змінної. |
| \(y\)-вісь | \(y\)-вісь - це вертикальна числова лінія декартової площини. |
| Позначення координат | Координатна точка - це опис місця розташування на координатній площині. Координатні точки зазвичай записуються у вигляді,\((x, y)\) де\(x\) горизонтальна відстань від початку, а y - вертикальна відстань від початку. |
| Координатна площина | Координатна площина - це сітка, утворена горизонтальною цифровою лінією і вертикальною цифровою лінією, які перетинаються в\((0, 0)\) точці, яка називається початком. Координатна площина також називається декартовою площиною. |
| Відображення | Відбиття - це перетворення, яке перевертає фігуру на координатній площині через задану лінію без зміни форми або розміру фігури. |
| Обертання | Обертання - це перетворення, яке перетворює фігуру на координатній площині на певну кількість градусів навколо заданої точки без зміни форми або розміру фігури. |
| Трансформація | Перетворення певним чином переміщує фігуру на координатну площину. |
| Переклад | Переклад - це перетворення, яке ковзає фігуру по координатній площині без зміни її форми, розміру або орієнтації. |
Додаткові ресурси
Інтерактивний елемент
Практика: Відображення фігур
Реальний світ: Дзеркало, Дзеркало