8.12: Програмне забезпечення геометрії та графічні обертання

Last updated

Oct 27, 2022
Save as PDF
- 8.11: Правила ротації
- 8.13: Визначення відображення

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Графік повернуто зображення з урахуванням попереднього зображення та кількості градусів. Виконайте обертання за допомогою Geogebra.

Чотирикутник $WXYZ$ має координати $W(−5,−5)$ , $X(−2,0), \(Y(2,3)$ і $Z(−1,3)$ . Намалюйте чотирикутник на декартовій площині. Поверніть зображення $110^{\circ}$ проти годинникової стрілки навколо точки $X$ . Показувати отримане зображення.

Графіки обертань

У геометрії трансформація - це операція, яка переміщує, перевертає або змінює фігуру для створення нової форми. Обертання - це приклад перетворення, коли фігура обертається навколо певної точки (званої центром обертання), певної кількості градусів.

Наразі для того, щоб графікувати обертання загалом, ви будете використовувати програмне забезпечення для геометрії. Це дозволить повертати будь-яку фігуру на будь-яку кількість градусів щодо будь-якої точки. Є кілька поширених обертань, які добре знати, як обійтися без програмного забезпечення геометрії, наведені в таблиці нижче.

Центр обертання	Кут повороту	Передзображення (точка $P$ )	Повернене зображення (точка $P′$ )
$(0, 0)$	$90^{\circ}$ (або\ (−270^ {\ circ})	\ (P\))» клас = "lt-k12-6056"> $(x,y)$	\ (P′\))» клас = "lt-k12-6056"> $(−y,x)$
$(0, 0)$	$180^{\circ}$ (або $−180^{\circ}$ )	\ (P\))» клас = "lt-k12-6056"> $(x,y)$	\ (P′\))» клас = "lt-k12-6056"> $(−x,−y)$
$(0, 0)$	$270^{\circ}$ (або $−90^{\circ}$ )	\ (P\))» клас = "lt-k12-6056"> $(x,y)$	\ (P′\))» клас = "lt-k12-6056"> $(y,−x)$

Давайте намалюємо попереднє зображення та зображення та належним чином позначимо кожне для наступного перетворення:

Лінія, $\overline{AB}$ $(-4, 2)$ проведена від до, $(3, 2)$ була повернута навколо початку під кутом $90^{\circ}$ CW.

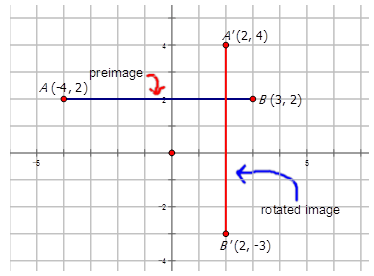
Ф-д_4е8293Б23Ф1108 ЕБ46Б23Б1Б 739624АЦ7421ДББДК195594564A7E+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Тепер давайте намалюємо та позначимо повернуте зображення для наступних обертань:

Алмаз $ABCD$ обертається $145^{\circ}$ CCW щодо походження, щоб сформувати зображення $A′B′C′D′$ .

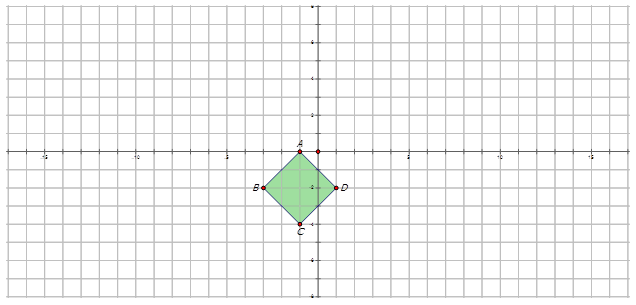
F-д_867Д3Е90Е4Б46С 1Дек 081С2Ф1Д13Е0АД 1ЕБФ 473Е1ЕБ5Б37Ф3АСС87+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{2}$

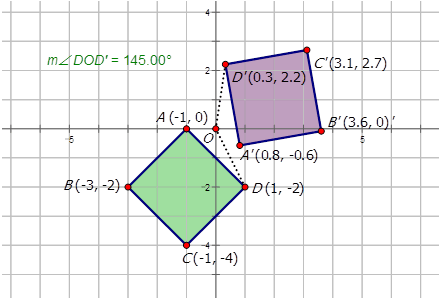
F-D_15917E414351 ліжко 4 особи БК 51Б0ФЦ 65С528909378997202E4FDAD295E+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Зверніть увагу на напрямок проти годинникової стрілки.

Наступний малюнок обертається навколо вихідного $200^{\circ}$ CW, щоб зробити повернуте зображення.

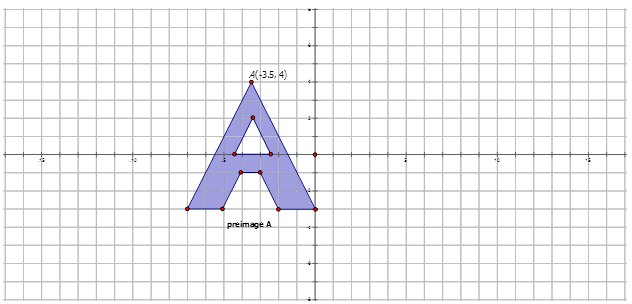
F-D_6489C7A10DF04071 DC CADD8D756F2C77 BEA669F2716B1ACE4E0745A5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{4}$

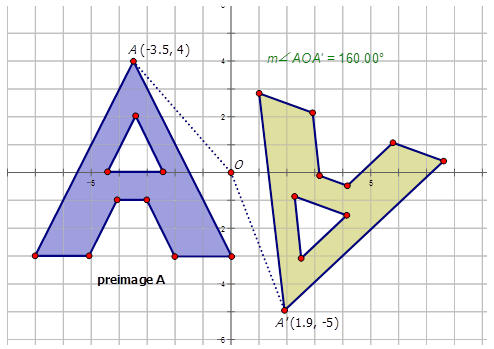
F-D_B1EB7FCD75Ф30БК2 Б8523Д839684 ФЕ764А 62 ФЕБ 2Д35428A7CB3AF8+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{5}$

Зверніть увагу, що напрямок обертання - проти годинникової стрілки, тому кут повороту дорівнює $160^{\circ}$ .

Приклад $\PageIndex{1}$

Раніше вас запитали про чотирикутник $WXYZ$ має координати $W(−5,−5)$ , $X(−2,0)$ , Y (2,3)\) і $Z(−1,3)$ . Намалюйте чотирикутник на декартовій площині. Поверніть зображення $110^{\circ}$ проти годинникової стрілки навколо точки X\). Показувати отримане зображення.

Рішення

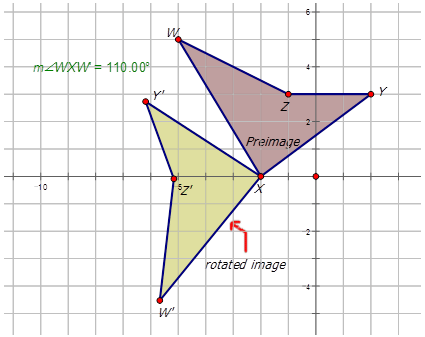
Ф-Д_3ФФ 27Б 70435Е 89ДФ 832СБ2242 АБ8 ФБ 65ДФ 515Ф1Б579891D4F9+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{6}$

Приклад $\PageIndex{2}$

Лінія, $\overline{ST}$ $(-3, 4)$ проведена від до, $(-3, 8)$ була повернута $60^{\circ}$ CW навколо точки $S$ . Намалюйте попереднє зображення та зображення та належним чином позначте кожен.

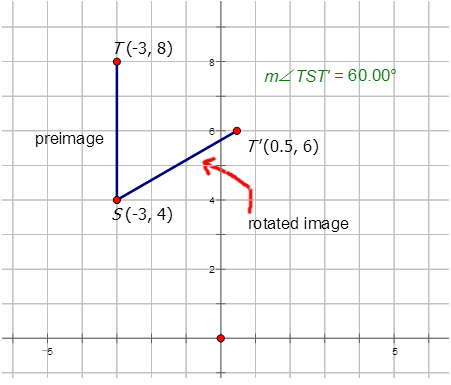
F-D_9A247Е66473АФ0Д0Е6Б8 КБКА69 ДФЕ 2А7587Б495Ф2623199Б2Д49Е8С+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{7}$

Рішення

Зверніть увагу, що напрямок кута знаходиться за годинниковою стрілкою, тому вимірювання кута є $60^{\circ}$ CW або $−60^{\circ}$ .

Приклад $\PageIndex{3}$

Багатокутник нижче був повернутий $155^{\circ}$ CCW щодо походження. Намалюйте повернуте зображення та належним чином позначте кожне.

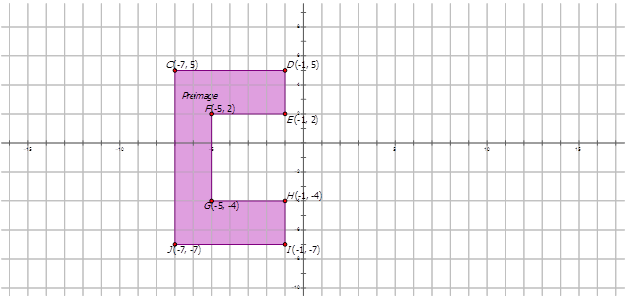
Ф-Д_880А2Ф3С197Е 88037Д4 АФ 3ДФ 22000108Б3429Ф09Ф91023А185CFBC2+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{8}$

Рішення

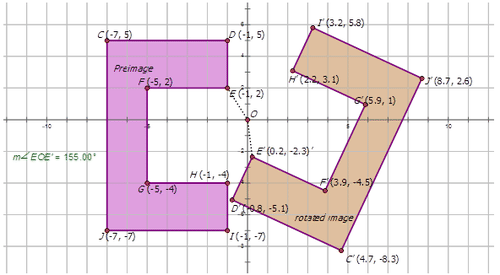
Зверніть увагу, що напрямок кута проти годинникової стрілки, тому вимірювання кута - $155^{\circ}$ CCW або $155^{\circ}$ .

Приклад $\PageIndex{4}$

Пурпурний п'ятикутник обертається навколо точки А $225^{\circ}$ . Знайдіть координати фіолетового п'ятикутника. На схемі намалюйте і позначте повернутий п'ятикутник.

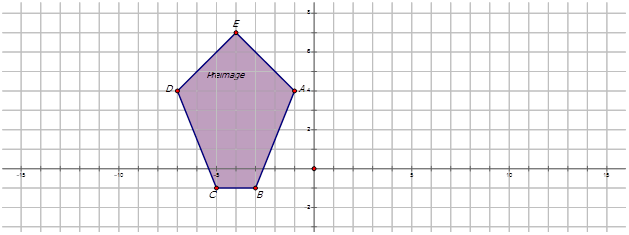
F-д_д9ф2С73 Е75Е6361С623ЕЕ4128С2ФА68А44Е0Б743Е5А2С6362A72E72E+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{10}$

Рішення

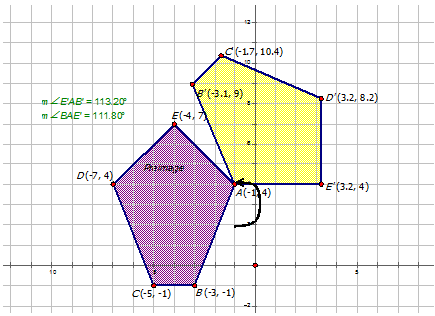
Ф-Д_181564900Ф7Ф7АА9С2CF034 БК БК 27754БК 89БК 96171Ф7398ДФББ+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{11}$

Міра $\angle BAB′=m\angle BAE′+m\angle E′AB′$ . Тому $\angle BAB′=111.80^{\circ} +113.20^{\circ}$ або $225^{\circ}$ . Зверніть увагу, що напрямок кута проти годинникової стрілки, тому вимірювання кута - $225^{\circ}$ CCW або $225^{\circ}$ .

Рецензія

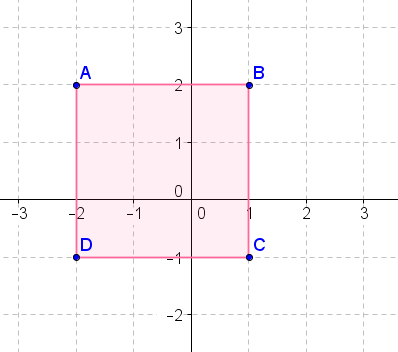
F-D_234 АФДФ 1317423С6Ф313С6Е1127АЦ511ДА 750 Б753685Ф77ФА1 Каф1С1+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{12}$

Поверніть вищевказану фігуру $90^{\circ}$ за годинниковою стрілкою навколо початку.
Поверніть вищевказану фігуру $270^{\circ}$ за годинниковою стрілкою навколо початку.
Поверніть наведену вище цифру $180^{\circ}$ про походження.

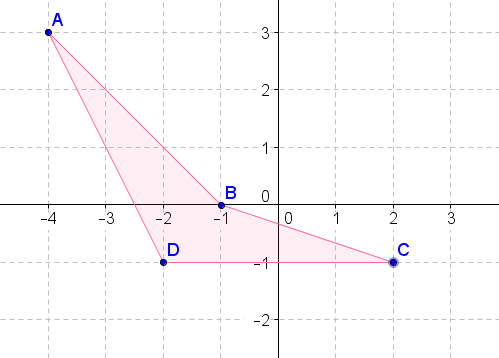
Ф-Д_4Ф6233Ф7СА960Б07С4А34Д7 БК 4 БК 94232С3ББ7 АФАД 60C012C860D61+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{13}$

Поверніть вищевказану фігуру $90^{\circ}$ проти годинникової стрілки навколо початку.
Поверніть вищевказану фігуру $270^{\circ}$ проти годинникової стрілки навколо початку.
Поверніть наведену вище цифру $180^{\circ}$ про походження.

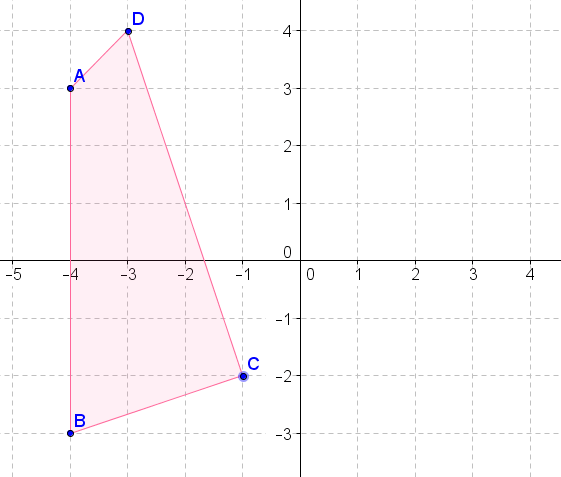
F-д_00дБ51Ф 117c77256 де 686а 27748 CDFA88c7f0ed0E633a59a3F89DA32+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{14}$

Поверніть вищевказану фігуру $90^{\circ}$ за годинниковою стрілкою навколо початку.
Поверніть вищевказану фігуру $270^{\circ}$ за годинниковою стрілкою навколо початку.
Поверніть наведену вище цифру $180^{\circ}$ про походження.

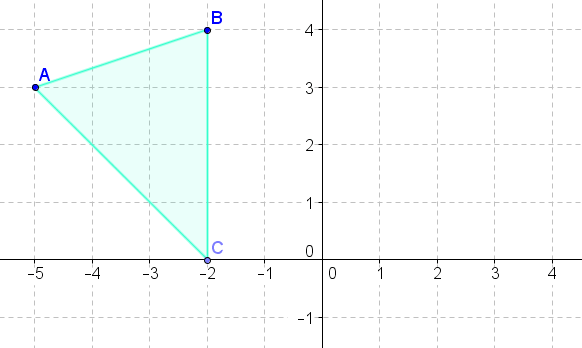
F-D_7A0999108D4A8 ДДД ДДД 2Д12Е9 ДБК 80С751Д5Д5Д6ДЦК076D52A0C96C0DC+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{15}$

Поверніть вищевказану фігуру $90^{\circ}$ проти годинникової стрілки навколо початку.
Поверніть вищевказану фігуру $270^{\circ}$ проти годинникової стрілки навколо початку.
Поверніть наведену вище цифру $180^{\circ}$ про походження.

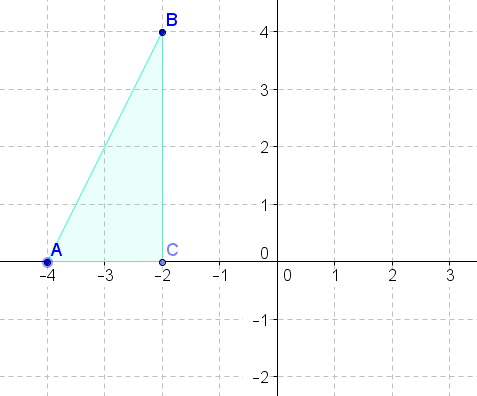
Ф-д_А0БД1Е4 Фе 9000Д0Б093449Е2КА6308318278563Ф9БДА50Д72А99+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{16}$

Поверніть вищевказану фігуру $90^{\circ}$ за годинниковою стрілкою навколо початку.
Поверніть вищевказану фігуру $270^{\circ}$ за годинниковою стрілкою навколо початку.
Поверніть наведену вище цифру $180^{\circ}$ про походження.

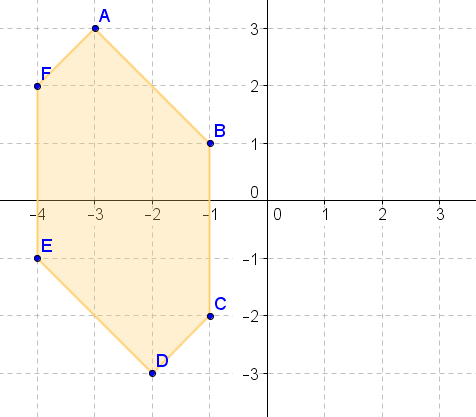
Ф-Д_СА485Б559ББ107Ф944 ДБ21СБ 24БДД30Б0ЕЕЕЕЕ1Ф9 Ф9 FADC2416114+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{17}$

Поверніть вищевказану фігуру $90^{\circ}$ проти годинникової стрілки навколо початку.
Поверніть вищевказану фігуру $270^{\circ}$ проти годинникової стрілки навколо початку.
Поверніть наведену вище цифру $180^{\circ}$ про походження.

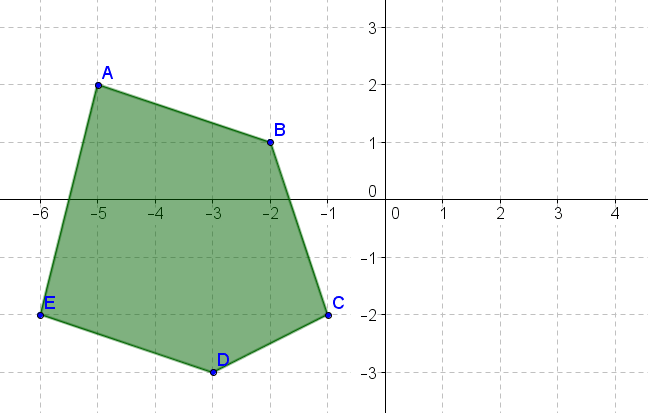
Ф-д_АБ7С6С52Е913Ф82КС35Ф16Б ФС69Б8С2Б49ФБКБЦ9082С37ФД4469Б2+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{18}$

Поверніть вищевказану фігуру $90^{\circ}$ за годинниковою стрілкою навколо початку.
Поверніть вищевказану фігуру $270^{\circ}$ за годинниковою стрілкою навколо початку.
Поверніть наведену вище цифру $180^{\circ}$ про походження.

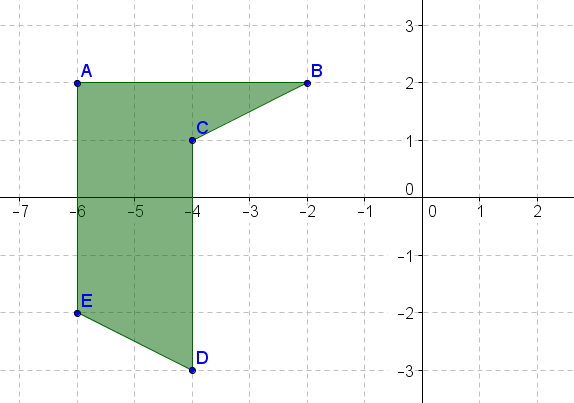
F-D_B9 ДФ9Е5Ф525629АФ 5ФА89480А949Ф75Б148Ф600Е1Б7А4405Д326C4E+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{19}$

Поверніть вищевказану фігуру $90^{\circ}$ проти годинникової стрілки навколо початку.
Поверніть вищевказану фігуру $270^{\circ}$ проти годинникової стрілки навколо початку.
Поверніть наведену вище цифру $180^{\circ}$ про походження.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.8.

Лексика

Термін	Визначення
Обертання	Обертання - це перетворення, яке перетворює фігуру на координатній площині на певну кількість градусів навколо заданої точки без зміни форми або розміру фігури.

Додаткові ресурси

Практика: програмне забезпечення геометрії та графічні обертання