8.8: Програми перекладу в колі подібності

Last updated

Oct 27, 2022
Save as PDF
- 8.7: Геометрія програмного забезпечення для перекладів
- 8.9: Позначення перекладу

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Вирішуйте проблеми, пов'язані з співвідношеннями та колами та використовуйте перетворення, щоб показати кола схожі.

Кола і подібність

Шон має два кола, один з радіусом 1 дюйм і інший радіусом 3 дюйми.

Яке співвідношення між радіусами кіл?
Що таке масштабний коефіцієнт між двома колами?
Яке співвідношення між окружностями кіл?
Яке співвідношення між площами кіл?
Яке відношення площі та коефіцієнти окружності мають відношення до масштабного коефіцієнта?

Коло - це сукупність точок, рівновіддалених від заданої точки. Радіус кола, r, - це відстань від центру кола до кола. Розмір кола залежить тільки від його радіуса.

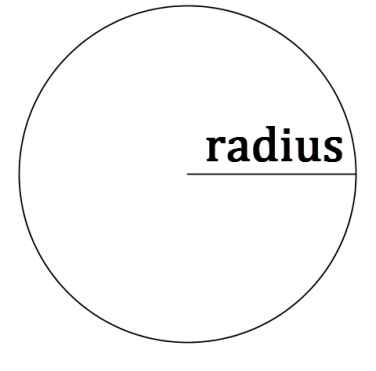
Дві фігури схожі, якщо подібність перетворення буде нести одну фігуру в іншу. Перетворення подібності - це одне або кілька жорстких перетворень з подальшим розширенням. На прикладах ви покажете, що перетворення подібності існує між будь-якими двома колами і тому всі кола схожі.

Згадайте дві важливі формули, пов'язані з колами:

Окружність (периметр) кола: $C=2\pi r$
Площа кола: $A=\pi r^{2}$

Після того, як ви показали, що всі кола схожі, ви вивчите, як пов'язані кола та області кіл.

Доведення подібності кола

Розглянемо коло $A$ , центрований у точці $A$ з радіусом $r_A$ , і коло $D$ , центрований у точці $D$ з радіусом $rD$ . Виконайте жорстке перетворення, щоб довести точку $A$ до точки $D$ .

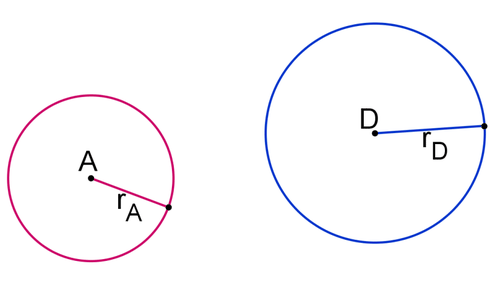
Намалюйте вектор від точки $A$ до точки $D$ . Переведіть Circle $A$ \) уздовж вектора, щоб створити коло $A′$ . Зауважте, що $r_A \cong r′_A$ .

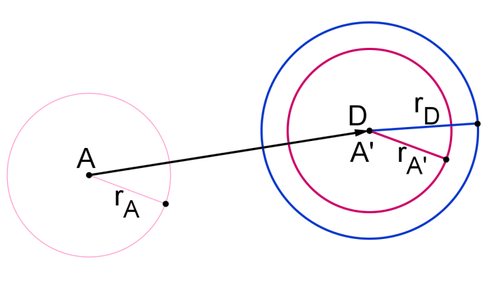
Розширити коло $A$ , щоб зіставити його на коло $D$ . Чи можете ви бути впевнені, що кола схожі?

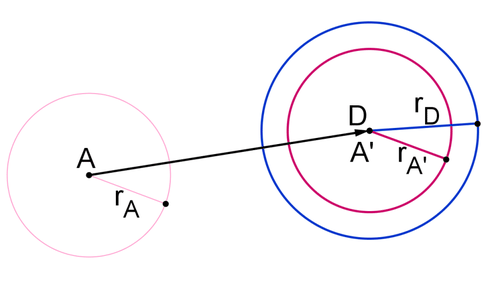
Оскільки розмір кола повністю визначається його радіусом, ви можете використовувати радіуси, щоб знайти правильний масштабний коефіцієнт. Розширити коло $A′$ близько точки $A′$ на коефіцієнт масштабу $\dfrac{r_D}{r_{A′}}$ .

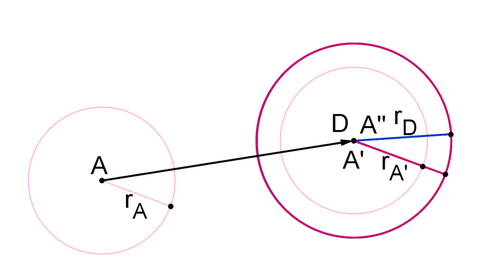
Коло $A′′$ - це той же коло $A$ коло $D$ . Ви можете бути впевнені в цьому, тому що $r_{A′′}=\dfrac{r_D}{r_{A′}} \cdot r_{A′}=r_{D}$ і точка $A′′$ така ж, як точка $D$ . Оскільки коло визначається його центром і радіусом, якщо два кола мають однаковий центр і радіус, то вони є одним і тим же колом.

Це означає, що коло $A$ схоже на коло $D$ , тому що перетворення подібності (переклад потім розширення) відображено коло $A$ на коло D\).

Коло $A$ і коло $D$ були двома випадковими колами. Це доводить, що в цілому всі кола схожі.

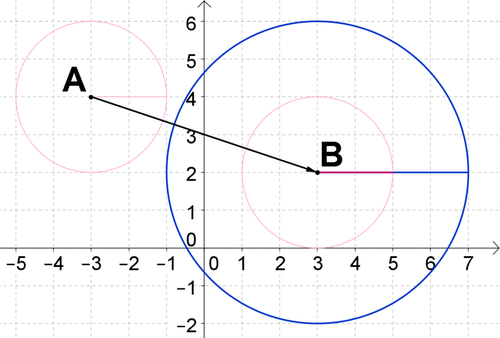
3. Покажіть, що коло $A$ з центром $(−3, 4)$ та радіусом 2 схоже на коло $B$ з центром $(3, 2)$ та радіусом 4.

Перевести коло $A$ вздовж вектора від $(−3, 4)$ до $(3, 2)$ . Потім розширте зображення навколо його центру на коефіцієнт масштабу 2. Ви матимете зіставлене коло $A$ на коло $B$ з перетворенням подібності. Це означає, що коло $A$ схожий на коло $B$ .

Приклад $\PageIndex{1}$

Раніше вам давали проблему про Шона і двох його колах.

Шон має два кола, один з радіусом 1 дюйм і інший радіусом 3 дюйми.

Яке співвідношення між радіусами кіл?
Що таке масштабний коефіцієнт між двома колами?
Яке співвідношення між окружностями кіл?
Яке співвідношення між площею кіл?
Яке відношення площі та коефіцієнти окружності мають відношення до масштабного коефіцієнта?

Рішення

Співвідношення між радіусами дорівнює 31.
Масштабний коефіцієнт існує тому, що будь-які два кола схожі. Ви можете використовувати радіуси для визначення масштабного коефіцієнта. Співвідношення між радіусами є $\dfrac{3}{1}$ таким чином коефіцієнт масштабу $\dfrac{3}{1}=3$ .
Окружність меншого кола дорівнює $C=2\pi (1)=2\pi$ . Окружність більшого кола дорівнює $C=2\pi (3)=6\pi$ . Співвідношення між окружностями дорівнює $\dfrac{6\pi}{2\pi}=\dfrac{3}{1}$ .
Площа меншого кола дорівнює $A=\pi (1)2=\pi$ . Площа більшого кола дорівнює $A=\pi(3)^2=9\pi$ . Співвідношення між площами є $\dfrac{9\pi}{\pi}=\dfrac{9}{1}$ . Зауважте, що $\dfrac{9}{1}=(\dfrac{3}{1})^2$ .
Коефіцієнт площі - це коефіцієнт масштабу в квадраті, оскільки площа - це двовимірне вимірювання. Коефіцієнт окружності дорівнює масштабному коефіцієнту, оскільки окружність - це одновимірне вимірювання.

Приклад $\PageIndex{2}$

Покажіть, що Коло $A$ з центром $(−1,7)$ та радіусом 2 схоже на Коло $B$ з центром $(4,6)$ та радіусом 3.

Рішення

Перевести Коло $A$ вздовж вектора від $(−1,7)$ до $(4,6)$ . Потім, розгорніть зображення навколо його центру з коефіцієнтом масштабування $\dfrac{3}{2}$ . У вас буде зіставлено коло $A$ на коло $B$ з перетворенням подібності. Це означає, що Circle $A$ схожий на Circle $B$ .

Приклад $\PageIndex{3}$

Ставлення окружності кола $D$ до окружності кола $C$ дорівнює $\dfrac{4}{3}$ . Яке співвідношення їх площ?

Рішення

Співвідношення окружностей таке ж, як і коефіцієнт масштабування. Тому коефіцієнт масштабування є $\dfrac{4}{3}$ . Співвідношення площ - коефіцієнт масштабу в квадраті. Тому співвідношення площ є $(\dfrac{4}{3})^2=\dfrac{16}{9}$ .

Приклад $\PageIndex{4}$

Ставлення площі кола $F$ до площі кола $E$ дорівнює $\dfrac{9}{4}$ . Яке співвідношення їх радіусів?

Рішення

Співвідношення площ - коефіцієнт масштабу в квадраті. Тому коефіцієнт масштабування є $\sqrt{\dfrac{9}{4}}=\dfrac{3}{2}$ . Співвідношення радіусів таке ж, як і коефіцієнт масштабу, тому відношення радіусів є $\dfrac{3}{2}$ .

Рецензія

Для #1 - #10 покажіть, що кола схожі, описуючи перетворення подібності, необхідне для відображення одного кола на інше.

Коло $A$ з центром (2,7)\) і радіусом 4. Коло $B$ з центром $(1,−4)$ і радіусом 3.
Коло $A$ з центром (6,4)\) і радіусом 3. Коло $B$ з центром $(−5,6)$ і радіусом 5.
Коло $A$ з центром (1,4)\) і радіусом 2. Коло $B$ з центром $(3,−2)$ і радіусом 7.
Коло $A$ з центром (8,1)\) і радіусом 6. Коло $B$ з центром $(6,−4)$ і радіусом 8.
Коло $A$ з центром (−2,10)\) і радіусом 3. Коло $B$ з центром $(−1,−4)$ і радіусом 6.
Коло $A$ з центром (−1,5) і радіусом 4. Коло $B$ з центром $(−1,5)$ і радіусом 5.
Коло $A$ з центром (−4, −2) та радіусом 1. Коло $B$ з центром $(1,8)$ і радіусом 4.
Коло $A$ з центром (10,3) і радіусом 5. Коло $B$ з центром $(4,2)$ і радіусом 8.
Коло $A$ з центром (12,4) і радіусом 10. Коло $B$ з центром $(12,4)$ і радіусом 12.
Коло $A$ з центром (−7,6) і радіусом 9. Коло $B$ з центром $(1,−4)$ і радіусом 9.
Відношення окружності Коло $A$ до окружності Коло $B$ дорівнює $\dfrac{2}{3}$ . Яке співвідношення їх радіусів?
Відношення площі Кола $A$ до площі Кола $B$ дорівнює $\dfrac{6}{1}$ . Яке співвідношення їх радіусів?
Відношення радіуса Кола $A$ до радіуса Кола $B$ дорівнює $\dfrac{5}{9}$ . Яке співвідношення їх площ?
Відношення площі Кола $A$ до площі Кола $B$ дорівнює $\dfrac{12}{5}$ . Яке співвідношення їх окружностей?
Щоб показати, що будь-які два кола схожі, вам потрібно виконати переклад та/або розширення. Чому вам ніколи не потрібно буде використовувати відбиття або обертання?

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 8.1.

Лексика

Термін	Визначення
Коло	Коло - це сукупність всіх точок на певній відстані від заданої точки в двох вимірах.
Дилатація	Зменшити або збільшити цифру відповідно до масштабного коефіцієнта - це розширення.
Радіус	Радіус кола - це відстань від центру кола до краю кола.
Жорстке перетворення	Жорстке перетворення - це перетворення, яке зберігає відстань і кути, воно не змінює розмір або форму фігури.
Трансформація подібності	Перетворення подібності - це одне або кілька жорстких перетворень з подальшим розширенням.

Додаткові ресурси

Інтерактивний елемент