8.10: Визначення обертання

Last updated

Oct 27, 2022
Save as PDF
- 8.9: Позначення перекладу
- 8.11: Правила ротації

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Перетворення, за допомогою яких фігура обертається навколо фіксованої точки для створення зображення.

обертань

Трансформація - це операція, яка рухає, перевертає або іншим чином змінює фігуру для створення нової фігури. Жорстке перетворення (також відоме як ізометрія або перетворення конгруентності) - це трансформація, яка не змінює розмір або форму фігури.

Жорсткі перетворення - це переклади, роздуми та обертання. Нова фігура, створена перетворенням, називається зображенням. Оригінальна фігура називається передзображенням. Якщо попередній образ є $A$ , то зображення буде $A′$ , сказано «простим». Якщо є зображення $A′$ , що буде позначено $A′′$ , сказав «подвійне просте».

Обертання - це перетворення, коли фігура обертається навколо фіксованої точки для створення зображення. Лінії, проведені від попереднього зображення до центру обертання і від центру обертання до зображення, утворюють кут повороту.

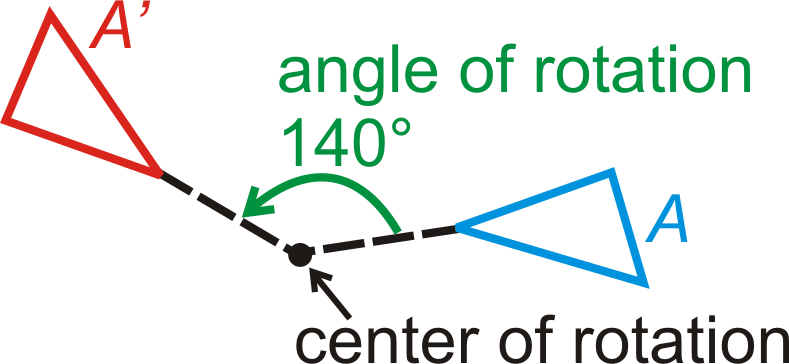
Ф-Д_5БД 378816240175Б57 АФБ 19БД4153808Д8 Цеб9185448Д5А41ККА5AD+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Хоча ми можемо повертати будь-яке зображення на будь-яку кількість градусів $90^{\circ}$ , $180^{\circ}$ а $270^{\circ}$ обертання є загальними і мають правила, які варто запам'ятати.

Обертання $180^{\circ}$ : $(x,y)\rightarrow (−x,−y)$

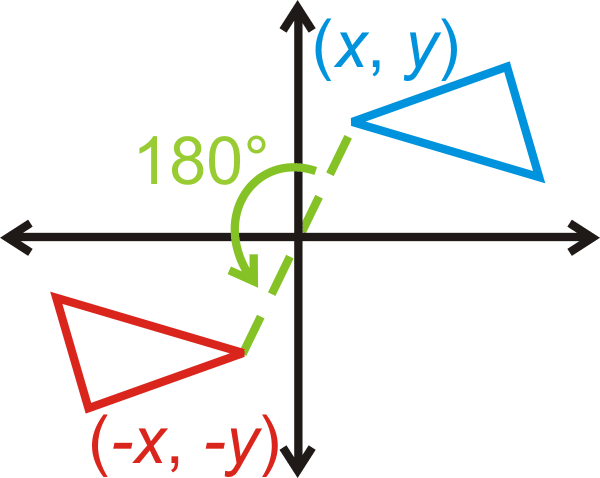
Ф-д_Б4ЕФ9052919А49Е54ЕА44А8ЕБ70С9Е1607220Ф7859 ДББ521864Е127+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{2}$

Обертання $90^{\circ}$ : $(x,y)\rightarrow (−y,x)$

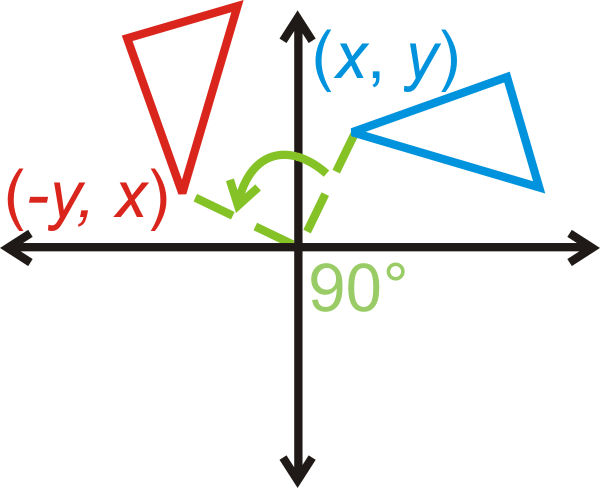
F-д_03349 БА 80СА27АФ7БФ 6 де 529СА4ДФ ДБ711ДФ 230232521052374Е7А05+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Обертання $270^{\circ}$ : $(x,y)\rightarrow (y,−x)$

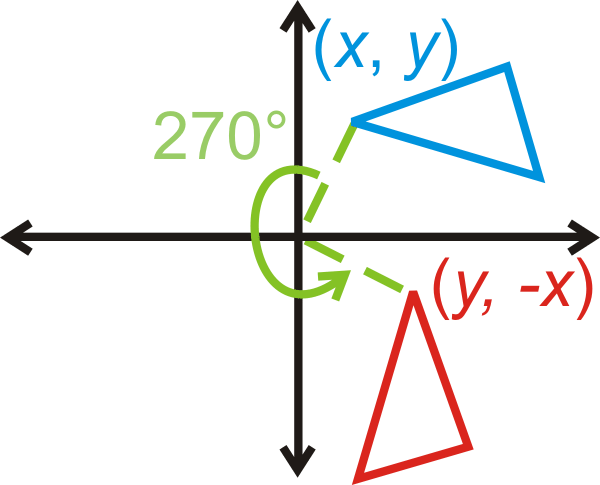
Ф-д_628ДФ 37АФД 1Б6174 ФФ 2Ф47С50Ф0Б169С69Б8630Ф6509Д8С1ЕЕ+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{4}$

Що робити, якщо вам дали координати чотирикутника, і вас попросили повернути цей чотирикутник $270^{\circ}$ навколо початку? Якими будуть його нові координати?

Приклад $\PageIndex{1}$

Обертання $80^{\circ}$ за годинниковою стрілкою - це те саме, що обертання проти годинникової стрілки?

Рішення

Є $360^{\circ}$ навколо точки. Отже, $80^{\circ}$ обертання за годинниковою стрілкою таке ж, як $360^{\circ}−80^{\circ}=280^{\circ}$ обертання проти годинникової стрілки.

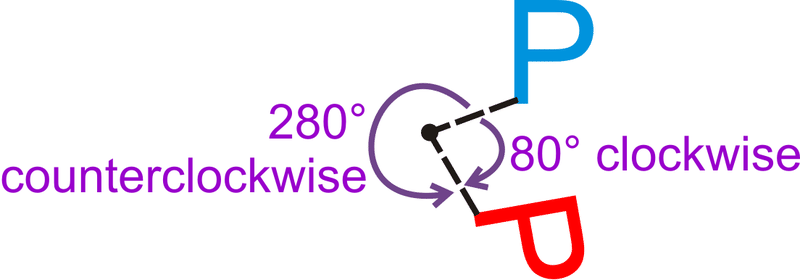F-д_454ФБД 0676А577134Ф216708838Б2АД 4ФБД71АЕ22Д11307С36Б209С8+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{6}$

Приклад $\PageIndex{2}$

Обертання\ (160^ {\ circ} проти годинникової стрілки таке ж, як і обертання за годинниковою стрілкою?

Рішення

$360^{\circ}−160^{\circ}=200^{\circ}$ обертання за годинниковою стрілкою

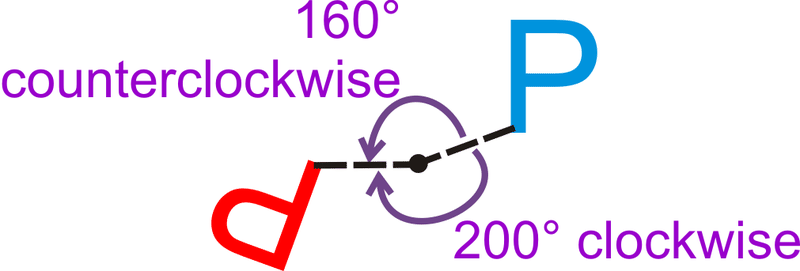
F-D_141 ЕБ82986 CF4FDD2ЕС570705378 EDC 76ЕЦДФ 6А274ЕС0А54Ф9E366+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{7}$

Приклад $\PageIndex{3}$

Обертати $\overline{ST} 90^{\circ}$ .

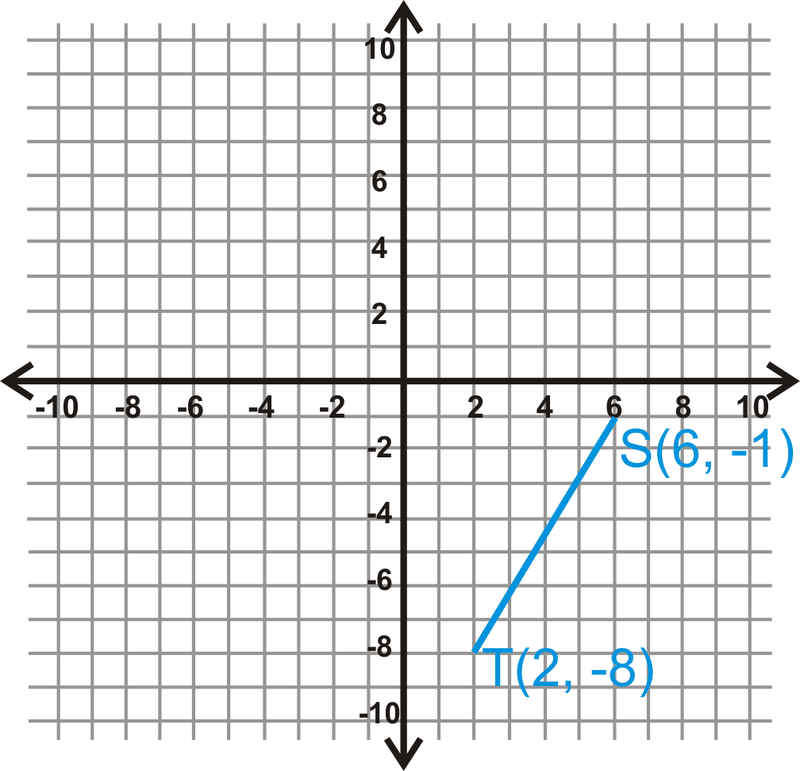
F-д_С9А 0 Мертвий 78 AB17b5167785F09d241c12df66c9d20afe 577F027D1CE+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{8}$

Рішення

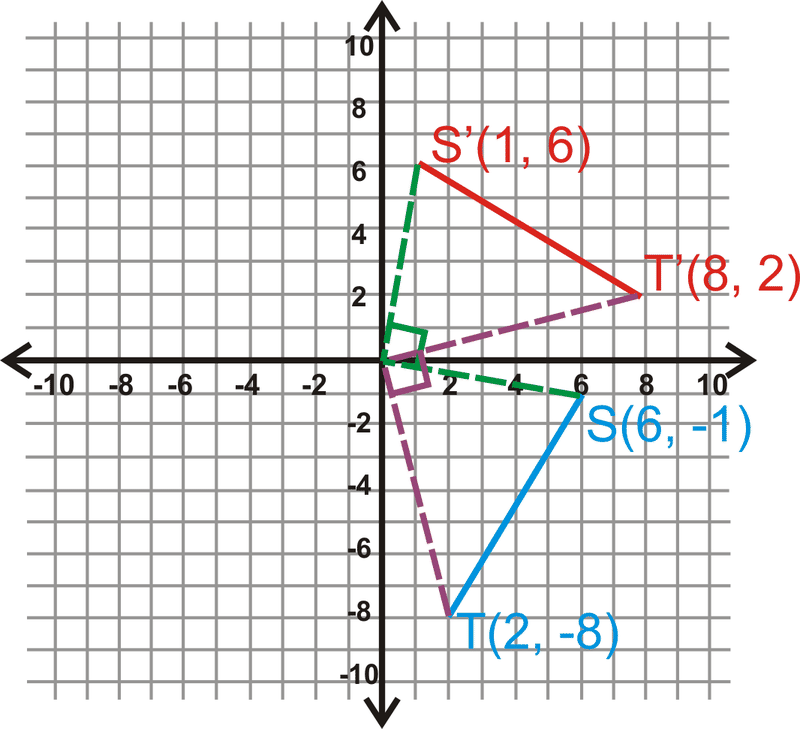
F-D_4649371723391Б5С19А7056С9А92Е621Б32А11Е898ФБ055ДЕА 4BEF8D+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{9}$

Приклад $\PageIndex{4}$

Обертання чотирикутника показано нижче. Що таке міра $x$ і $y$ ?

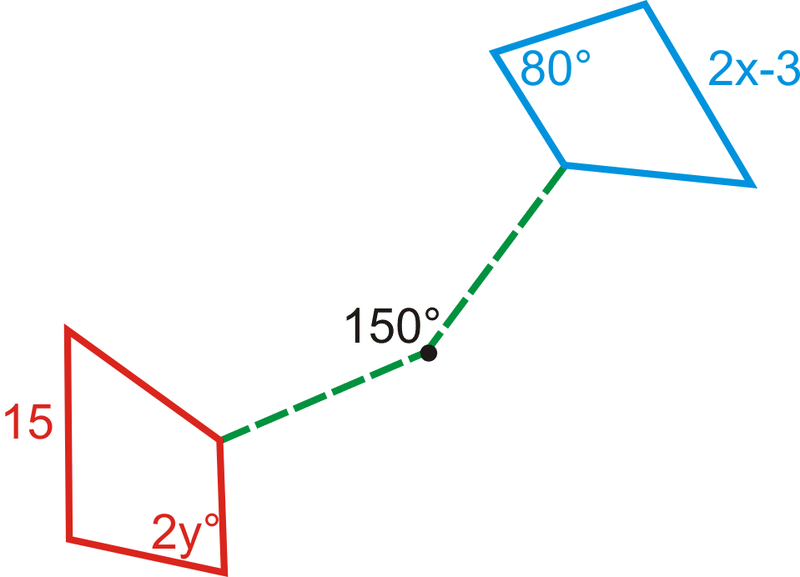
F-D_986C5537B9FBB3570F61219D5DCFB529D2A6CB0550F23996F8BA0C88+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{10}$

Рішення

Оскільки обертання створює конгруентні фігури, ми можемо встановити два рівняння для вирішення $x$ і $y$ .

\ (y=4\ begin {масив} {rr}
2 y=80^ {\ circ} & 2 x-3 = 15\\
y=40^ {\ circ} & 2 x = 18\\
& x = 9
\ кінець {масив}\)

Приклад $\PageIndex{5}$

Поворот $\Delta ABC$ , з вершинами $A(7,4)$ $B(6,1)$ , і $C(3,1)$ , $180^{\circ}$ про початок. Знайдіть координати $\Delta A′B′C′$ .

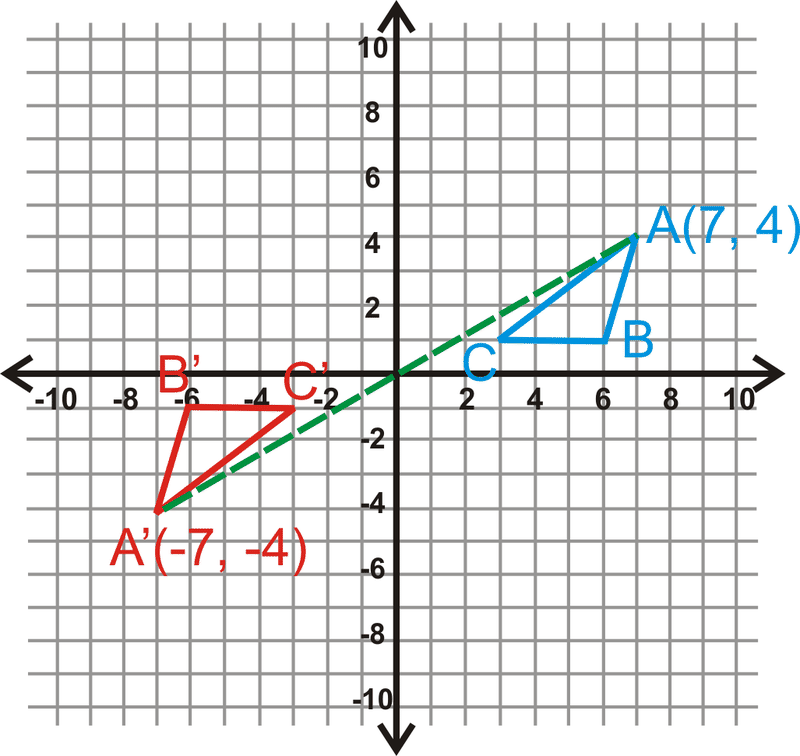
F-д_2106Б0082Б257143ФББ4А52С940АФ 65к8ФБ7396Б520Ф6824Б28С411+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{11}$

Рішення

Скористайтеся правилом вище, щоб знайти $\Delta A′B′C′$ .

$\begin{aligned}A(7,4)&\rightarrow A′(−7,−4) \\ B(6,1)&\rightarrow B′(−6,−1) \\ C(3,1)&\rightarrow C′(−3,−1)\end{aligned}$

Рецензія

У наведених нижче питаннях кожне обертання відбувається проти годинникової стрілки, якщо не вказано інше.

Якби ви повернули букву p 180^ {\ circ}\) проти годинникової стрілки, яка буква була б у вас?
Якби ви повернули букву p $180^{\circ}$ c\ (по годинниковій стрілці, яка буква була б у вас?
Обертання $90^{\circ}$ за годинниковою стрілкою те саме, що обертання проти годинникової стрілки?
Обертання $270^{\circ}$ за годинниковою стрілкою те саме, що обертання проти годинникової стрілки?
Обертання $210^{\circ}$ проти годинникової стрілки те саме, що обертання за годинниковою стрілкою?
Обертання $120^{\circ}$ проти годинникової стрілки те саме, що обертання за годинниковою стрілкою?
Обертання $340^{\circ}$ проти годинникової стрілки те саме, що обертання за годинниковою стрілкою?
Обертання фігури $360^{\circ}$ - це те саме, що інше обертання?
Чи має значення, повертаєте ви фігуру $180^{\circ}$ за годинниковою стрілкою або проти годинникової стрілки? Чому чи чому ні?
Малюючи повернуту фігуру та використовуючи транспортир, було б легше повертати фігуру $300^{\circ}$ проти годинникової стрілки або за годинниковою $60^{\circ}$ стрілкою? Поясніть свої міркування.

Поверніть кожну фігуру в координатній площині заданої міри кута. Центр обертання - це початок.

$180^{\circ}$

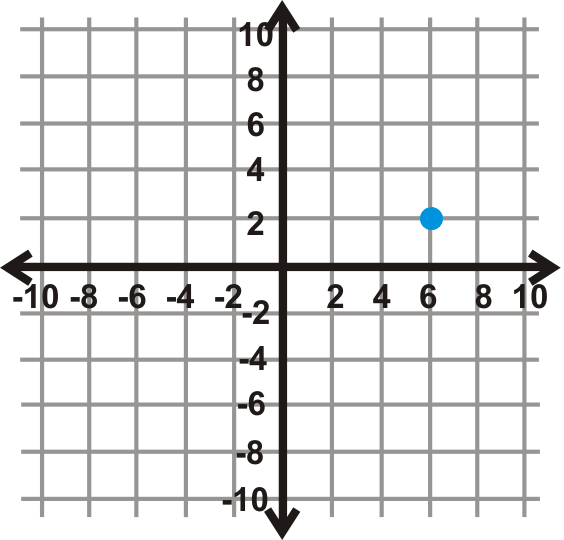
Малюнок $\PageIndex{12}$
$90^{\circ}$
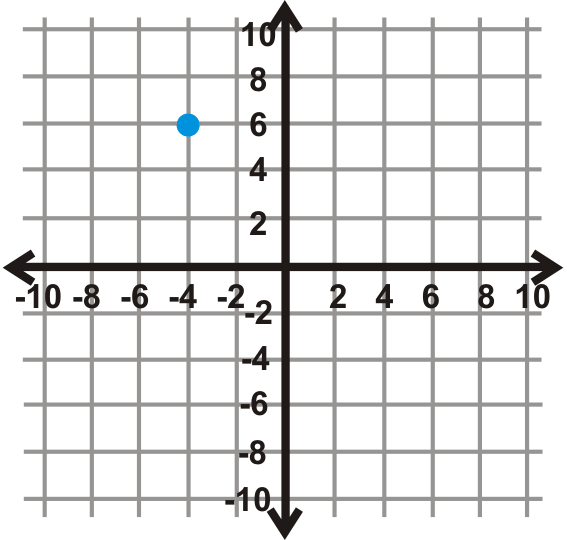Малюнок$\PageIndex{13}$
$180^{\circ}$

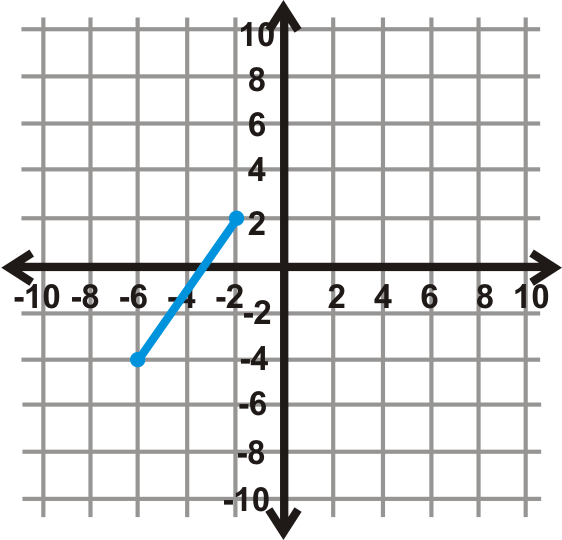
Малюнок $\PageIndex{14}$
$270^{\circ}$

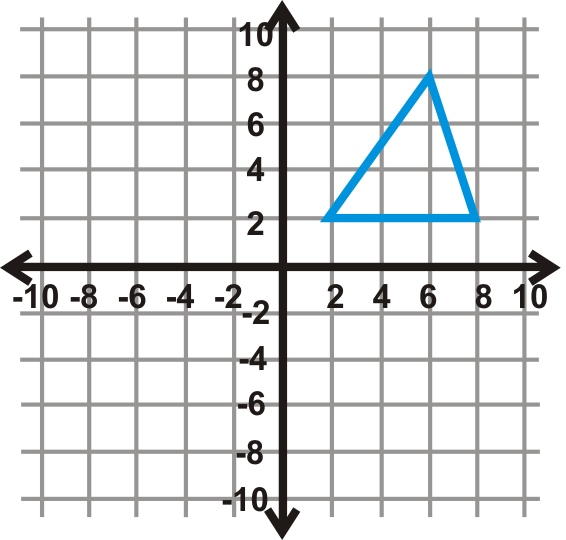
Малюнок $\PageIndex{15}$
$90^{\circ}$

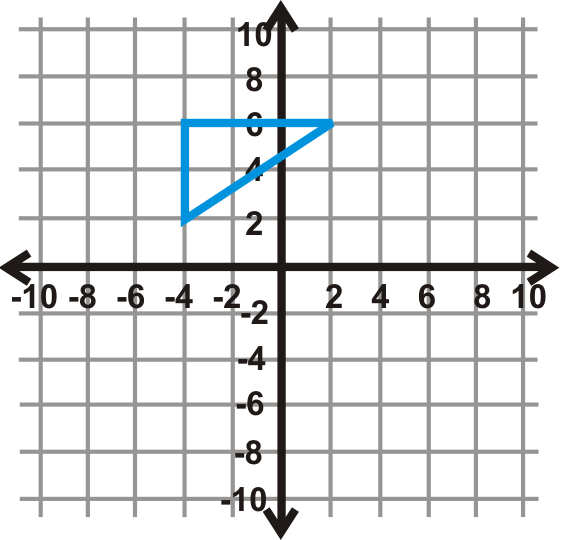
Малюнок $\PageIndex{16}$
$270^{\circ}$

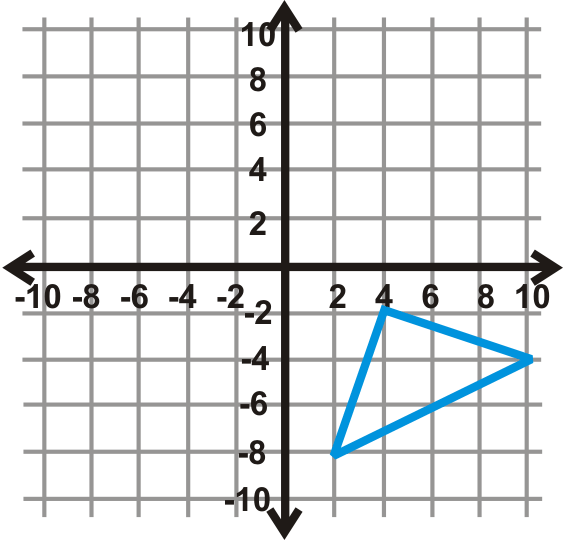
Малюнок $\PageIndex{17}$
$180^{\circ}$

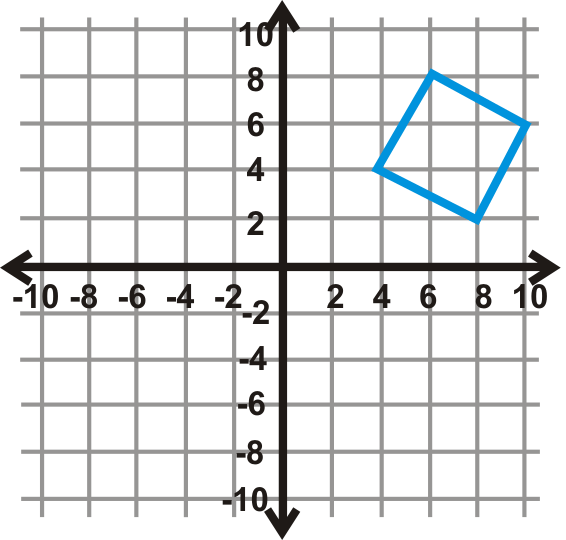
Малюнок $\PageIndex{18}$
$270^{\circ}$

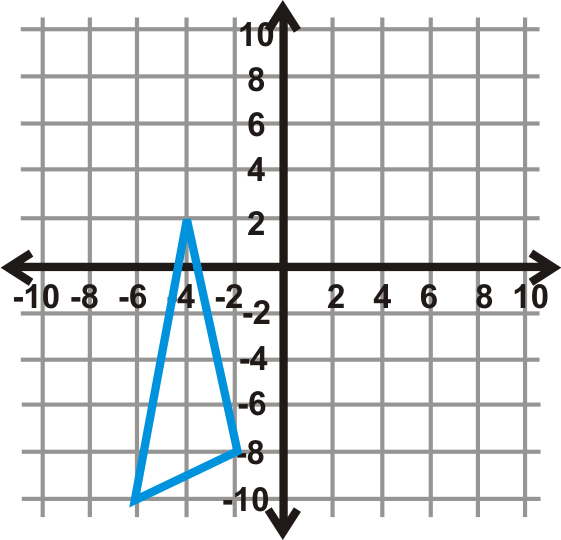
Малюнок $\PageIndex{19}$
$90^{\circ}$

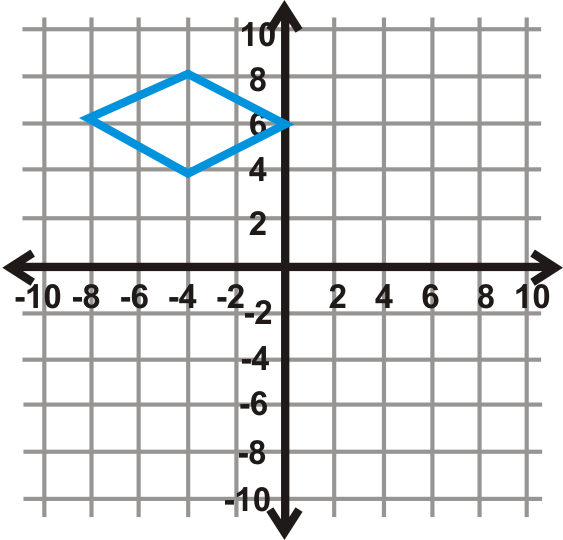
Малюнок $\PageIndex{20}$

Знайдіть міру $x$ в обертаннях нижче. Синя фігура - це преімідж.

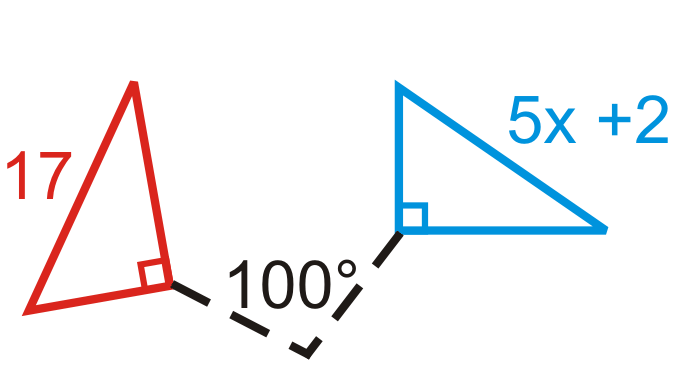
Малюнок $\PageIndex{21}$
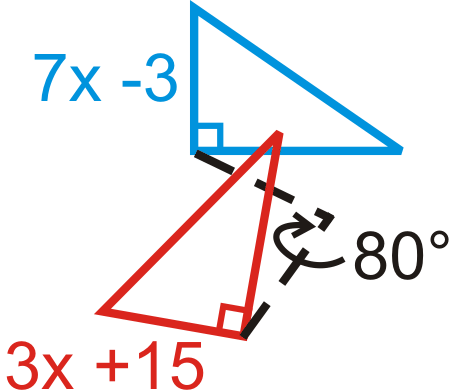
Малюнок $\PageIndex{22}$
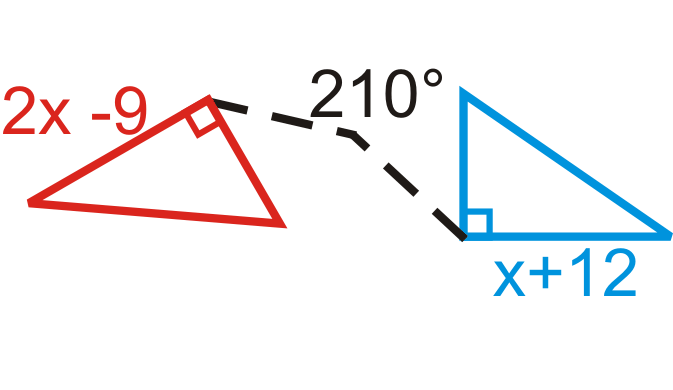
Малюнок $\PageIndex{23}$

Знайдіть кут повороту для графіків нижче. Центр обертання - це початок, а синя фігура - передзображення. Ваша відповідь буде $90^{\circ}$ $270^{\circ}$ , або $180^{\circ}$ .

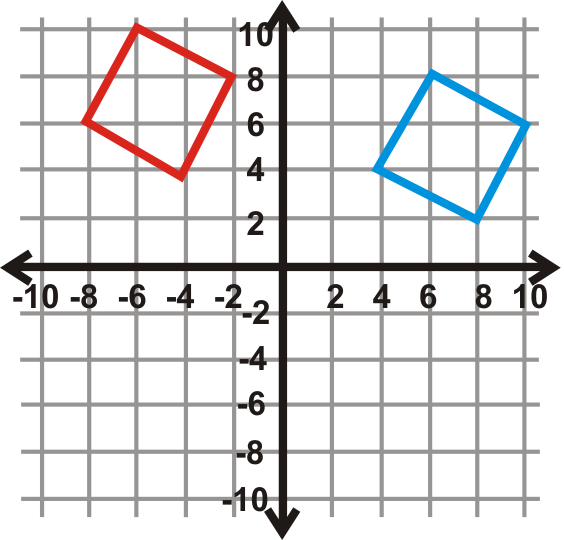
Малюнок $\PageIndex{24}$
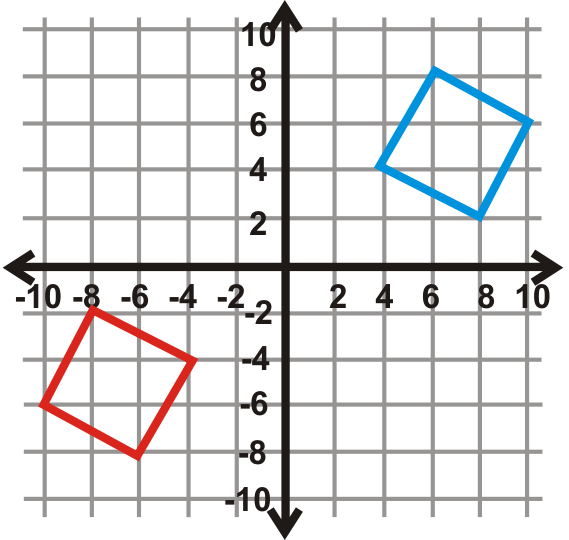
Малюнок $\PageIndex{25}$
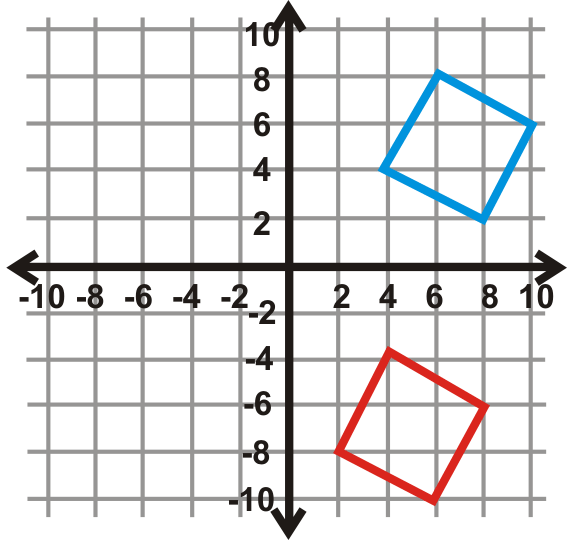
Малюнок $\PageIndex{26}$
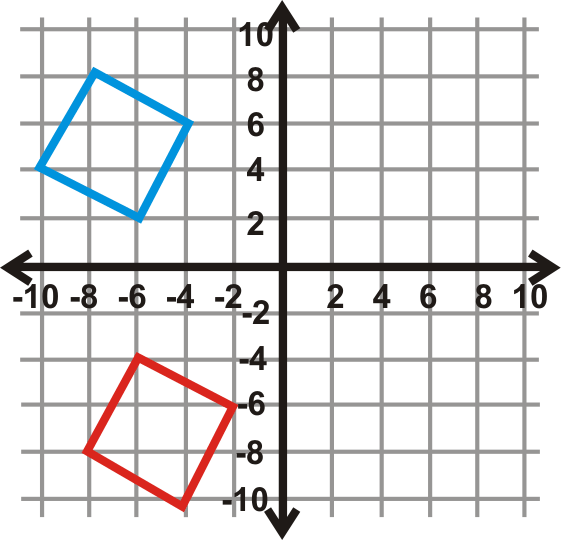
Малюнок $\PageIndex{27}$
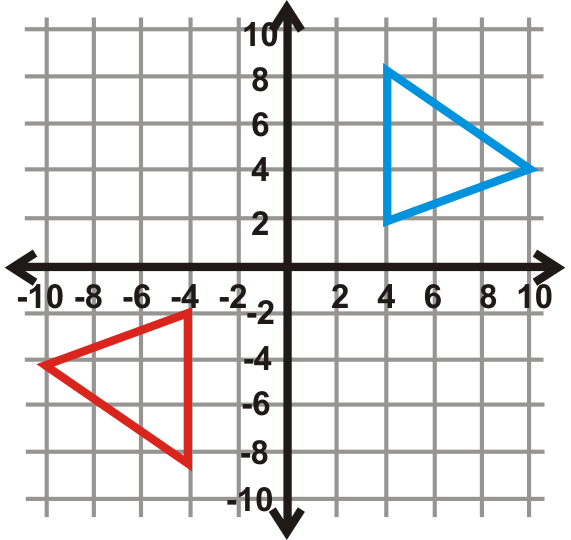
Малюнок $\PageIndex{28}$
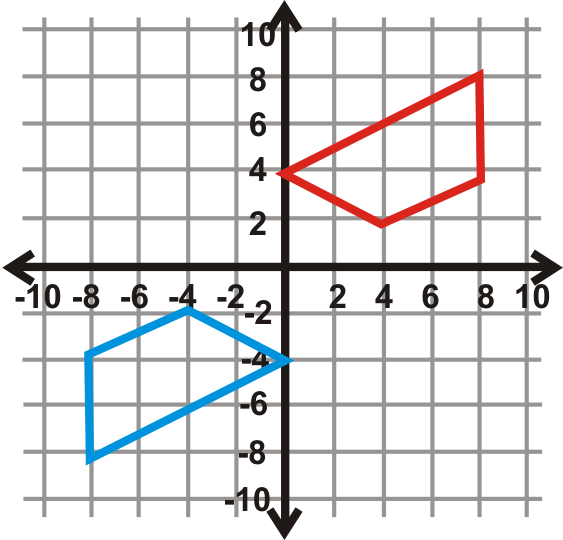
Малюнок $\PageIndex{29}$

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 12.4.

Лексика

Термін	Визначення
Центр обертання	При обертанні центр обертання - це точка, яка не рухається. Інша частина площини обертається навколо цієї нерухомої точки.
Зображення	Образ - це остаточний вигляд фігури після операції трансформації.
Походження	Походження - точка перетину осей x і y на декартовій площині. Координати початку координат є (0, 0).
Передзображення	Попереднє зображення - це оригінальний вигляд фігури в операції трансформації.
Обертання	Обертання - це перетворення, яке перетворює фігуру на координатній площині на певну кількість градусів навколо заданої точки без зміни форми або розміру фігури.
Жорстке перетворення	Жорстке перетворення - це перетворення, яке зберігає відстань і кути, воно не змінює розмір або форму фігури.

Додаткові ресурси

Інтерактивний елемент

Відео: Трансформація: принципи ротації - основні

Види діяльності: Ротації Питання обговорення

Навчальні посібники: Види трансформацій Навчальний посібник

Практика: Визначення обертання

Реальний світ: Радикальні обертання