8.6: Розсувні фігури

Last updated
Save as PDF

Page ID: 54937

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Використовуйте координати для переміщення фігур на координатній площині.

Класифікація трансформації

Місіс Гілкрест розробила спеціальну версію гри Морський бій. Її версія вимагає від учнів використовувати такі координати, як (1, 2), щоб вгадати місце розташування корабля. Кораблі стратегічно розміщені так, що кожен є перекладом іншого. Для того щоб гра була легшою для учнів, вона переводила кораблі на однакову відстань вгору або вниз, вправо або вліво. Якщо перший корабель знаходиться на (3, 6), (3, 7), (3, 8), а другий корабель перекладається 4 одиниці вправо і 4 одиниці вгору, які координати другого корабля?

У цьому понятті ви дізнаєтеся, як класифікувати перетворення.

Класифікація перетворень

Координатна площина являє собою подання двовимірного простору. Він має горизонтальну вісь, звану\(x\) -віссю, і вертикальну вісь, звану\(y\) -віссю. Ви можете робити графіки та переміщати геометричні фігури на координатній площині.

Запам'ятайте три типи перетворень: переклад, відображення і обертання.

Тепер давайте розглянемо виконання кожного типу перетворення в координатній площині.

Коли ви виконуєте переклади, ви ковзаєте фігуру вліво або вправо, вгору або вниз. Це означає, що на координатній площині координати вершин фігури будуть змінюватися. Погляньте на приклад нижче.

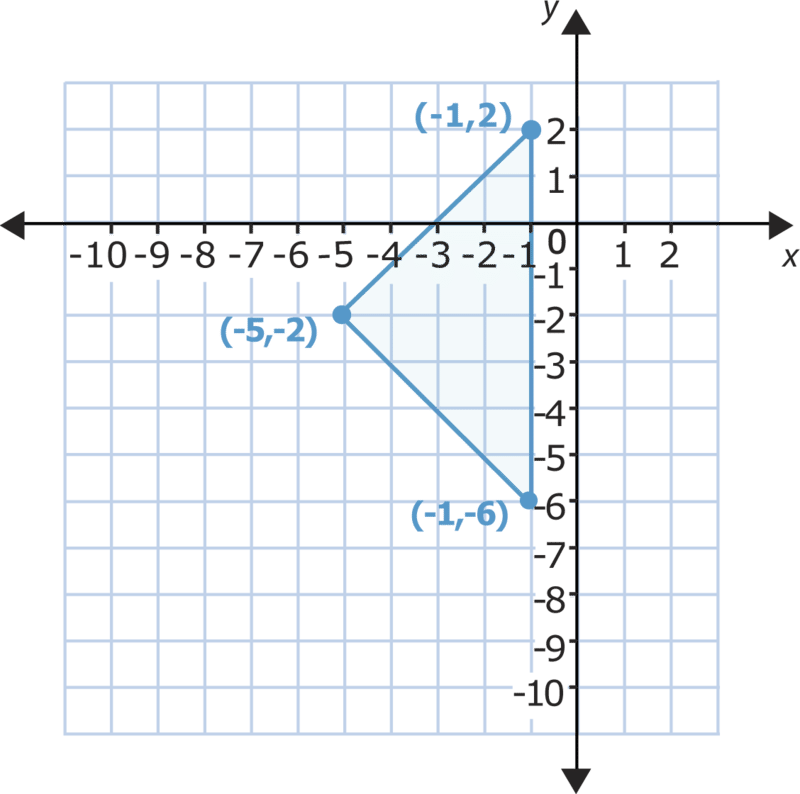
F-Д_Д3Е7378Б557А7А7А7С052БК8КС8СФ Ф 87Е96464E3978AD9F05E988B+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Тепер давайте розглянемо виконання перекладу або слайда цієї фігури.

Ви можете вибрати кількість місць, в які ви хочете перемістити трикутник і напрямок, в якому ви хочете його перемістити. Якщо ви посунете цей трикутник на 3 місця вниз, всі його вершини змістяться на 3 місця вниз по\(y\) осі -і\(y\) -координата в кожній парі зменшиться на 3.

Давайте розберемося, чому так відбувається.

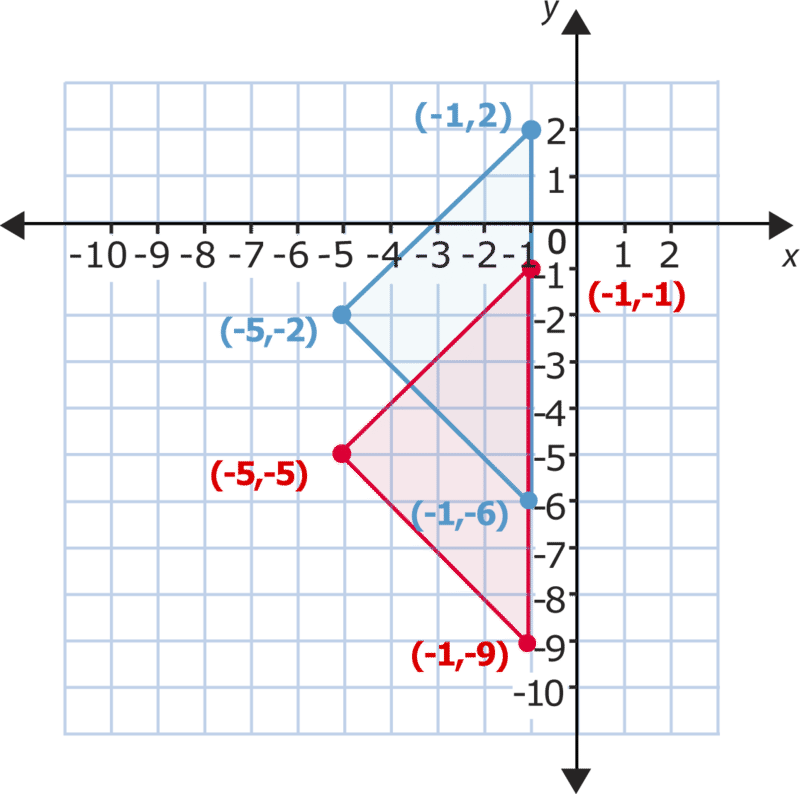
F-D_ADF 5597D615A8A2C7393 Баб 4Д32Ф8 БК8Б5Е58 ЕЕ0А14Д31167А+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Ви можете побачити зміни у всіх\(y\) -координатах. Порівняйте верхні пункти. \(y\)-координата зліва дорівнює 2. \(y\)-координата для відповідної точки в трикутнику після його переміщення дорівнює -1. \(y\)-координата зменшується на 3. Тепер порівняйте ліву точку кожного трикутника. \(y\)-coordinate спочатку дорівнює -2, а\(y\) -координата після перекладу дорівнює -5. Знову ж таки, різниця показує зміну -3 в\(y\) -координаті. Для останньої точки\(y\) -coordinate починається як -6 і зміщується до -9 після низхідного слайда. Для кожної точки\(y\) -координата зменшується на 3, тоді як\(x\) -координати залишаються однаковими.

Перекласти цифри можна і іншими способами. Як ви могли здогадатися, ви переміщуєте фігури вправо або вліво по координатній сітці за їх\(x\) -координатами. Ви також можете переміщати фігури по діагоналі, змінюючи їх координати x та\(y\) -координати. Таким чином, один із способів розпізнати переклади - порівняти їх моменти. \(x\)Координати змінюватимуться однаково, і\(y\) -координати змінюватимуться однаково.

Ось приклад того, як графувати переклад.

Просуньте наступну цифру на 5 місць вправо.

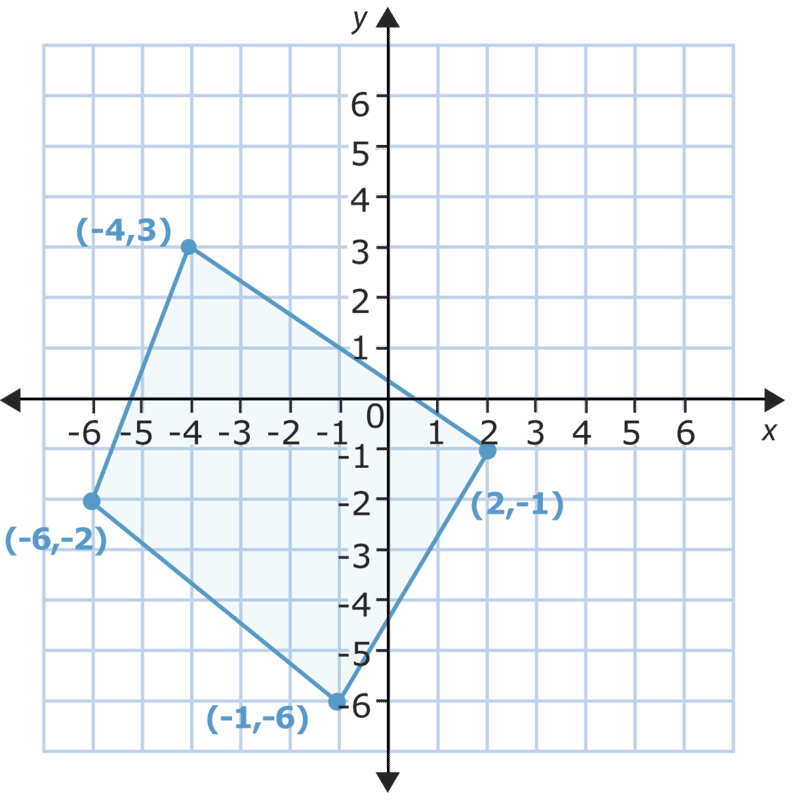
F-D_B1E77E80D963 АБ1Б 4А09Е4Д2СЕ858Б72067Д00Б6875Д06Б6084+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

У цьому перекладі ви перенесете фігуру вправо. Це означає, що\(x\) -координати для кожної точки змінюватимуться, але\(y\) -координати не будуть. Ви просто порахуєте 5 місць праворуч від кожної точки і робите нову точку.

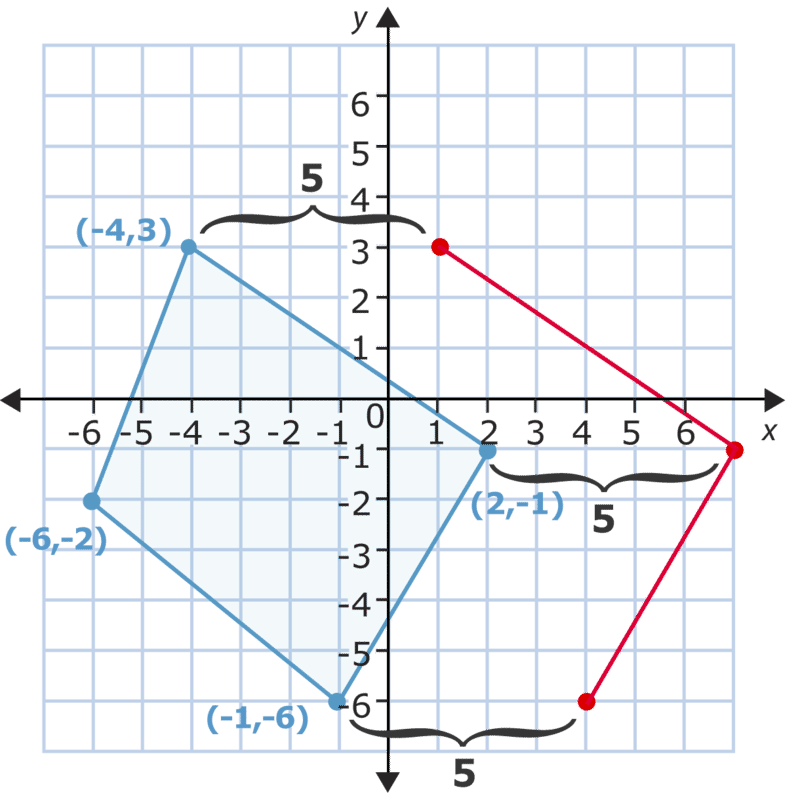
F-D_9D0ФД1 АФ 80027 АФА08д2660Б4ФД28С6Д477Ф6К 4805Ф4Б441+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Після того, як ви перемістіть кожну точку на 5 місць вправо, ви можете з'єднати їх, щоб зробити нову фігуру, яка показує переклад.

Ви можете перевірити, чи правильно ви виконали переклад, додавши 5 до кожної\(x\) -координати (тому що ви переїхали праворуч), а потім перевіривши їх на впорядковані пари малюнка, яку ви намалювали. Це називається позначенням координат. Зверніть увагу, що кожна точка представлена координатами.

\ (\ begin {масив} {lccc}
(-4,3) & (-6, -2) & (-1, -6) & (2, -1)\\
+5 & +5 & +5\\
(1,3) & (-1, -2) & (4, -6) & (7, -1)
\ end {масив}\)

Це точки, які ви намалювали, тож ви виконали переклад правильно.

Приклад\(\PageIndex{1}\)

Раніше вам давали завдання про місіс Гілкрест і її спеціальну версію гри Battleship.

Вона переводила кораблі на однакову відстань вгору або вниз, вправо або вліво. Якщо перший корабель знаходиться на (3, 6), (3, 7), (3, 8), а другий корабель перекладається 4 одиниці вправо і 4 одиниці вгору, які координати другого корабля?

Рішення

Спочатку запам'ятайте ознаки, пов'язані з рухом вправо і рухом вгору.

Праворуч - це рух у позитивному напрямку на\(x\) -осі, а вгору - це рух у позитивному напрямку на\(y\) -осі.

Далі додаємо ходи до координат.

(3+4, 6+4), (3+4, 7+4), (3+4, 8+4)

Потім запишіть нові вершини

(7, 10), (7, 11), (7, 12)

Координати другого корабля такі (7, 10), (7, 11), (7, 12).

Приклад\(\PageIndex{2}\)

Вирішити цю проблему.

Просуньте наступний малюнок на 4 місця вліво і 2 місця вгору.

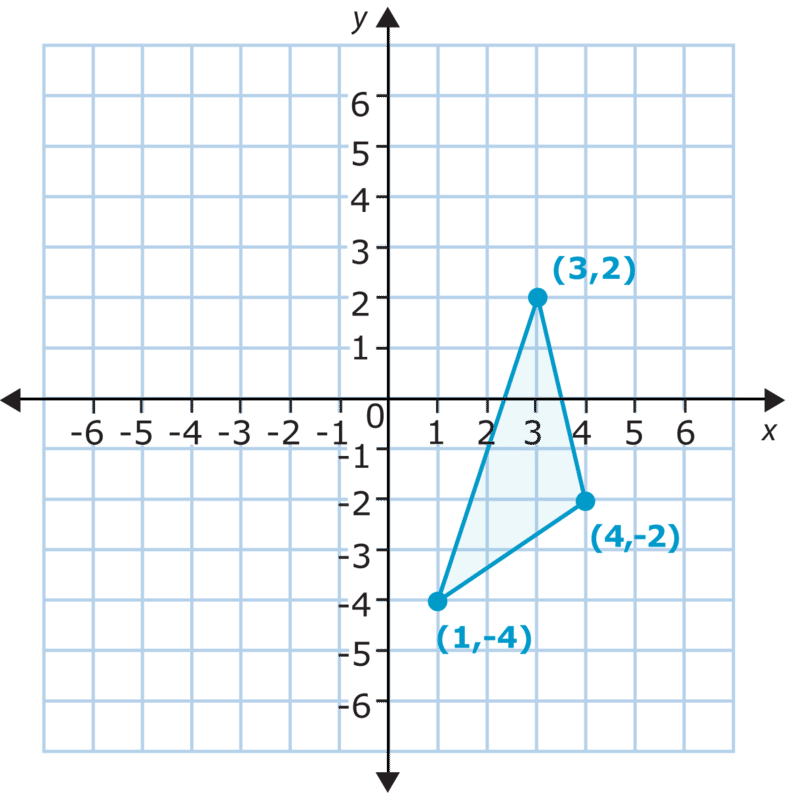
Ф-д_Е749FF2E7C98667769F8 CF6DDF330 ААЕ 372808BB8F662932E43BF+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Рішення

Спочатку наведіть графік нових точок.

Графік кожної точки, відрахувавши 4 місця зліва, а звідти 2 місця вгору.

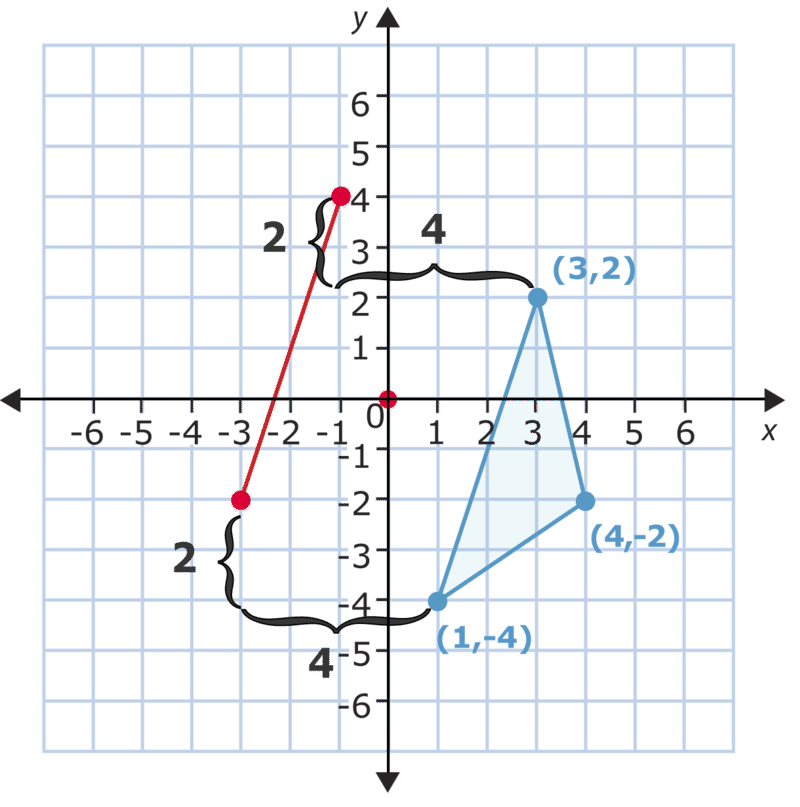
F-д_3Е6 АД 1205С5Д9Е38ЕБ947д37д 7212Б747Д4 Фа 3764С 2C59158415B+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{7}\)

Потім сформуйте новий трикутник.

З'єднайте нові точки.

Ви можете перевірити переклад, змінивши\(y\) координати\(x\) - і -у впорядкованих парах, а потім порівнявши їх з точками, які ви графували. Цього разу відніміть 4 з кожної\(x\) -координати і додайте 2 до кожної\(y\) -координати. Давайте подивимося, що вийде.

\ (\ begin {масив} {ccc}
(3,2) & (4, -2) & (1, -4)\\
-4+2 & -4+2 & -4+2\\
(-1,4) & (0,0) & (-3, -2)
\ end {масив}\)

Приклад\(\PageIndex{3}\)

Перевести трикутник\(\(ABC\)\) (0, 1), (1, 3), (4, 0) вгору 4.

Рішення

По-перше, запам'ятайте, чи є рух вгору по\(x\) -осі або\(y\) -осі.

Вгору - це рух по\(y\) -осі.

Далі додайте 4 до кожного з\(y\) -значень.

(0, 1+4), (1, 3+4), (4, 0+4)

Потім запишіть нові вершини.

(0, 5), (1, 7), (4, 4)

Новий трикутник має координати (0, 5), (1, 7), (4, 4).

Приклад\(\PageIndex{4}\)

Перекласти трикутник\(DEF\) (-3, 2), (1, 6), (2, 1) вниз 2.

Рішення

По-перше, запам'ятайте, чи є вниз рух по\(x\) -осі або\(y\) -осі.

Вниз - це хід по\(y\) -осі.

Далі відніміть по 2 з кожного з\(y\) -значень.

(-3, 2-2), (1, 6-2), (2, 1-2)

Потім запишіть нові вершини.

(-3, 0), (1, 4), (2, -1)

Новий трикутник має координати (-3, 0), (1, 4), (2, -1)

Приклад\(\PageIndex{5}\)

Перевести трикутник\(XYZ\) (-5, 4), (1, 8), (3, 5) вправо 3.

Рішення

По-перше, запам'ятайте, чи право - це рух на\(x\) -осі або\(y\) -осі.

Праворуч - це рух по\(x\) -осі.

Далі додаємо 3 до кожного\(x\) -значення.

(-5+3, 4), (1+3, 8), (3+3, 5)

Потім запишіть нові вершини

(-2, 4), (4, 8), (6, 5)

Новий трикутник має координати (-2, 4), (4, 8), (6, 5).

Рецензія

Визначте трансформації, показані нижче, як переклад, відображення або обертання.

F-д_42Е64С41ДББ 73 BE3558591026AD77Б569Е5С1947Б972Д5ББ05A29E9+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{8}\)

Правда чи брехня. Ця цифра була переведена на 5 місць вправо.

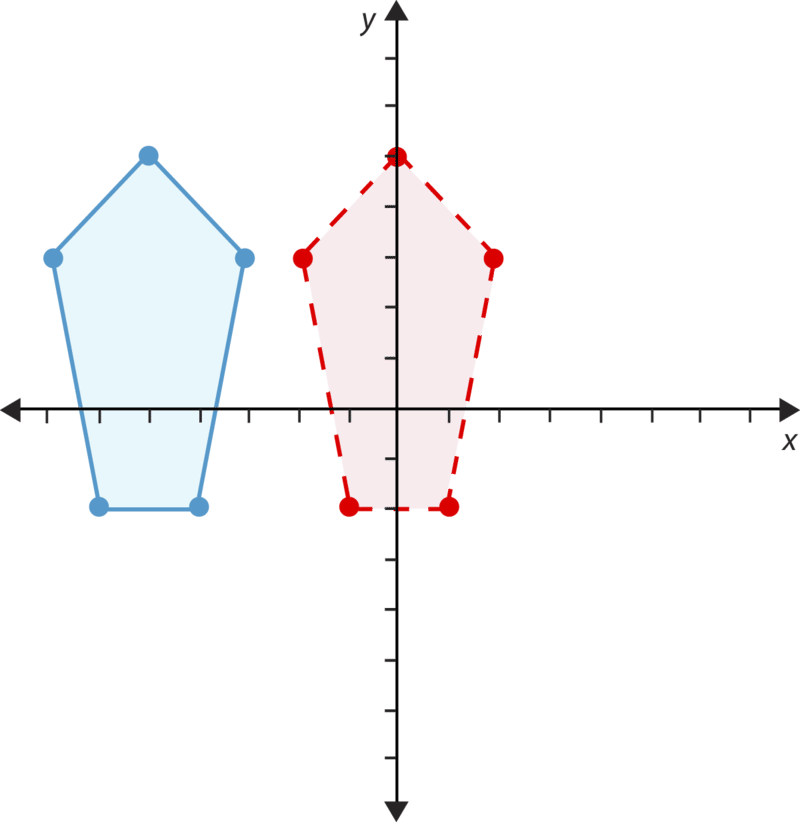
F-д_73ДДА 8 ФА3ЦС 283АФ 5А981 Д1БД5606А12Б74ФБ33БФ 07430Ф831+зображення_крихіткий+зображення_крихітка_крихіткий.PNG — Малюнок\(\PageIndex{9}\)

Переведіть кожну цифру вправо на 6 місць і вгору 1. Потім напишіть нові координати для фігури.

Трикутник\(DEF\) (-1, 2) (1, 6) (2, 1)
Трикутник\(DEF\) (-3, 2) (1, 6) (2, 1)
Трикутник\(DEF\) (0, 2) (1, 6) (2, 1)
Трикутник\(DEF\) (4, -2) (1, 6) (2, 1)
Трикутник\(DEF\) (5, 3) (1, 6) (2, 1)
Трикутник\(DEF\) (4, 4) (1, 6) (2, 1)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.18.

Ресурси

Лексика

Термін	Визначення
\(x\)-вісь	\(x\)-вісь - це горизонтальна вісь у координатній площині, зазвичай представляє значення вхідної або незалежної змінної.
\(y\)-вісь	\(y\)-вісь - це вертикальна числова лінія декартової площини.
Координатна площина	Координатна площина - це сітка, утворена горизонтальною цифровою лінією та вертикальною цифровою лінією, які перетинаються в точці (0, 0), яка називається початком. Координатна площина також називається декартовою площиною.
Трансформація	Перетворення певним чином переміщує фігуру на координатну площину.

Додаткові ресурси

Відео: Визначення квадранта точки системи координат

Практика: Розсувні фігури