8.5: Геометричний переклад

Зрозумійте переклади як рух кожної точки фігури на однаковій відстані в одному напрямку. Графічні зображення задані попередній образ і переклад.

Переклади

Трансформація - це операція, яка рухає, перевертає або іншим чином змінює фігуру для створення нової фігури. Жорстке перетворення (також відоме як ізометрія або перетворення конгруентності) - це трансформація, яка не змінює розмір або форму фігури.

Жорсткі перетворення - це переклади, роздуми та обертання. Нова фігура, створена перетворенням, називається зображенням. Оригінальна фігура називається передзображенням. Якщо попередній образ є$A$, то зображення буде$A′$, сказано «простим». Якщо є зображення$A′$, що буде позначено$A′′$, сказав «подвійне просте».

Переклад - це перетворення, яке переміщує кожну точку фігури на однакову відстань в одному напрямку. Наприклад, це перетворення переміщує паралелограм вправо на 5 одиниць і вгору на 3 одиниці. Написано$(x,y)\rightarrow (x+5, y+3)$.

Малюнок$\PageIndex{1}$

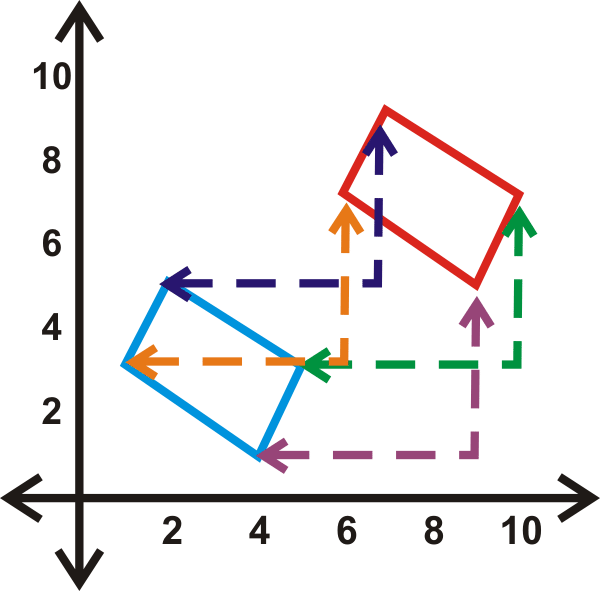
Що робити, якщо вам дали координати чотирикутника, і вас попросили перемістити цей чотирикутник 3 одиниці вліво і 2 одиниці вниз? Якими будуть його нові координати?

Приклад$\PageIndex{1}$

Трикутник$\Delta ABC$ має координати$A(3,−1)$,$B(7,−5)$ і$C(−2,−2)$. Переведіть$\Delta ABC$ вліво 4 одиниці вгору і 5 одиниць вгору. Визначаємо координати$\Delta A′B′C′$.

Малюнок$\PageIndex{2}$

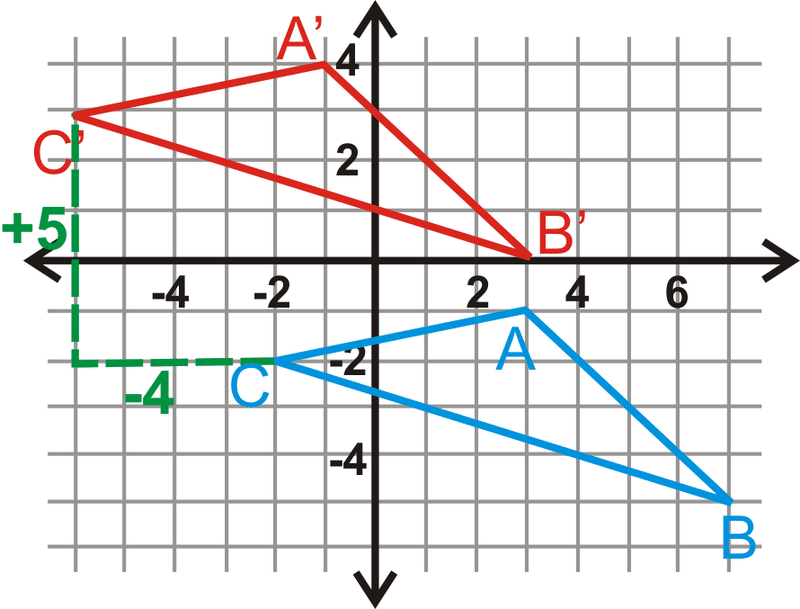
Рішення

Графік$\Delta ABC$. Для перекладу$\Delta ABC$ відніміть 4 з кожного$x$ значення і додайте 5 до кожного$y$ значення його координат.

$\begin{aligned} &A(3,−1)\rightarrow (3−4,−1+5)=A′(−1,4) \\ &B(7,−5)\rightarrow (7−4,−5+5)=B′(3,0) \\ &C(−2,−2)\rightarrow (−2−4,−2+5)=C′(−6,3) \end{aligned}$

Правило б було$(x,y)\rightarrow (x−4, y+5)$.

Приклад$\PageIndex{2}$

Використовуючи переклад$(x,y)\rightarrow (x+2, y−5)$, що таке образ$A(−6, 3)$?

Рішення

$A′(−4,−2)$

Приклад$\PageIndex{3}$

Граф квадрат$S(1,2)$$Q(4,1)$,,$R(5,4)$ і$E(2,5)$. Знайдіть зображення після перекладу$(x,y)\rightarrow (x−2,y+3)$. Потім проведіть графік і позначте зображення.

Рішення

Ми збираємося перемістити квадрат вліво на 2 і вгору на 3.

Малюнок$\PageIndex{3}$

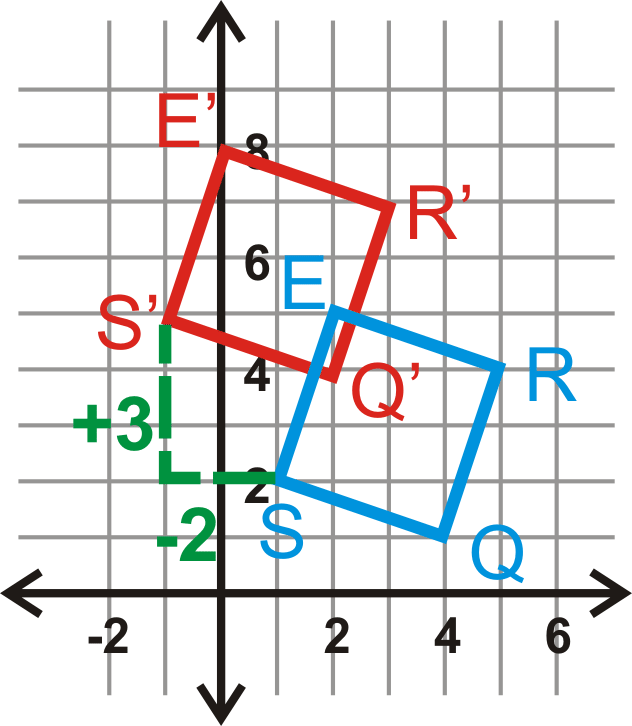
$\begin{aligned}(x,y)&\rightarrow (x−2,y+3) \\ S(1,2)&\rightarrow S′(−1,5) \\ Q(4,1)&\rightarrow Q′(2,4) \\ R(5,4)&\rightarrow R′(3,7) \\ E(2,5)&\rightarrow E′(0,8)\end{aligned}$

Приклад$\PageIndex{4}$

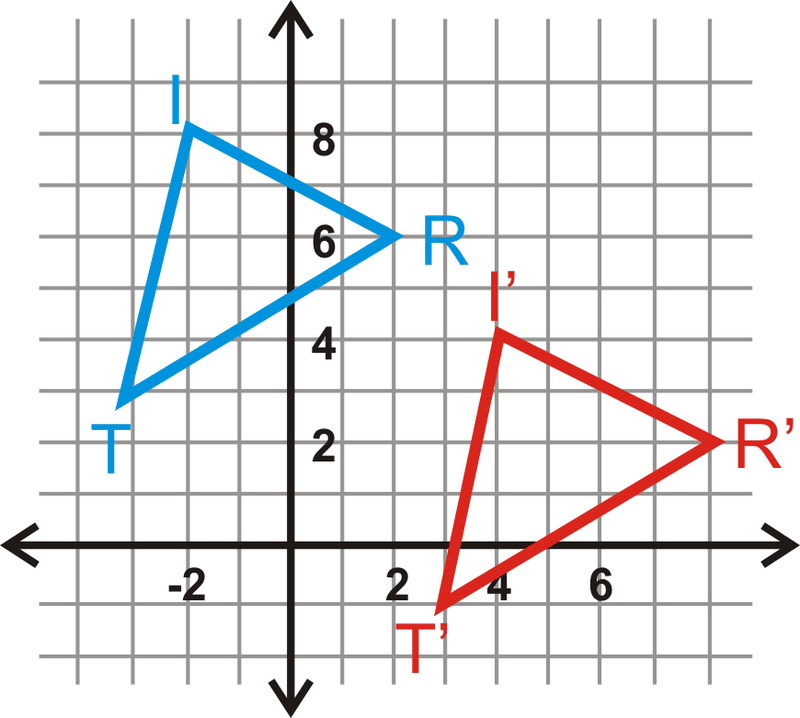
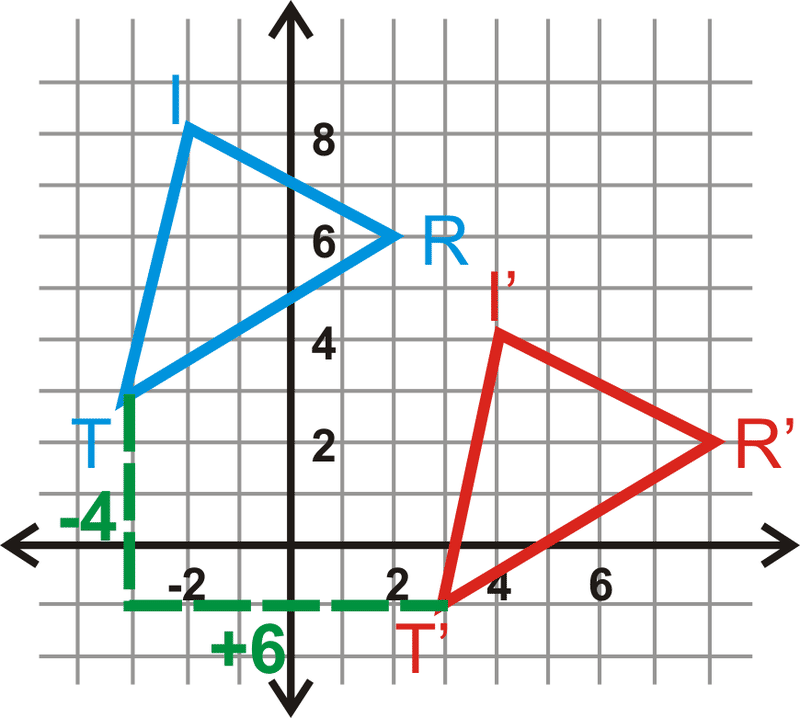
Знайдіть правило перекладу для$\Delta TRI$ to$\Delta T′R′I′$.

Рішення

Подивіться на рух від$T$ до$T′$. Правило перекладу є$(x,y)\rightarrow (x+6, y−4)$.

Малюнок$\PageIndex{4}$

Малюнок$\PageIndex{5}$

Рецензія

Використовуйте переклад$(x,y)\rightarrow (x+5, y−9)$ для питань 1-7.

1. Що таке образ$A(−1,3)$?
2. Що таке образ$B(2,5)$?
3. Що таке образ$C(4,−2)$?
4. Що таке образ$A′$?
5. Що таке преімідж$D′(12,7)$?
6. Що таке образ$A′′$?
7. Сюжет$A$$A′$,$A′′$,, і$A′′′$ з питань вище. Що ви помічаєте?

Вершини$\Delta ABC$ є$A(−6,−7)$,$B(−3,−10)$ і$C(−5,2)$. Знайдіть вершини$\Delta A′B′C′$, враховуючи наведені нижче правила перекладу.

8. $(x,y)\rightarrow (x−2, y−7)$
9. $(x,y)\rightarrow (x+11, y+4)$
10. $(x,y)\rightarrow (x, y−3)$
11. $(x,y)\rightarrow (x−5, y+8)$
12. $(x,y)\rightarrow (x+1, y)$
13. $(x,y)\rightarrow (x+3, y+10)$

У питаннях 14-17,$\Delta A′B′C′$ є образ$\Delta ABC$. Напишіть правило перекладу.

14. 

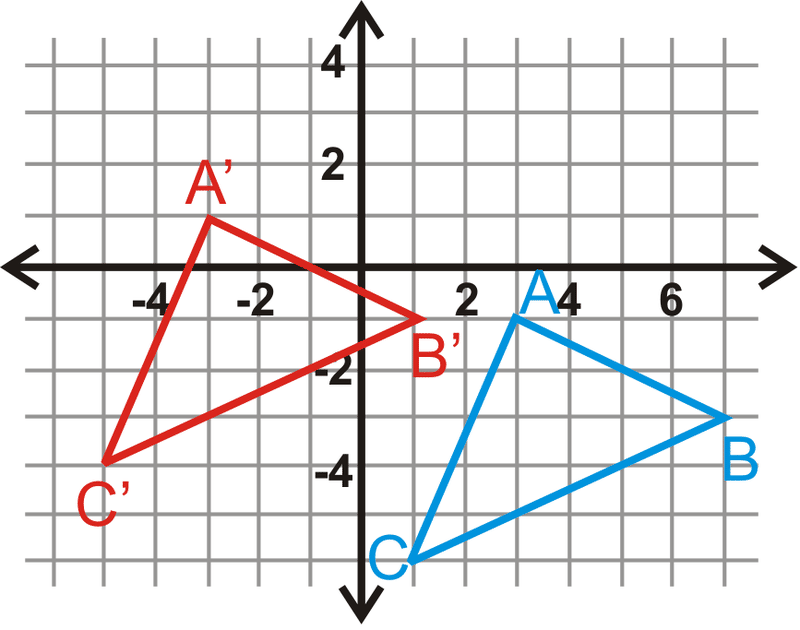
    Малюнок$\PageIndex{6}$

15. 

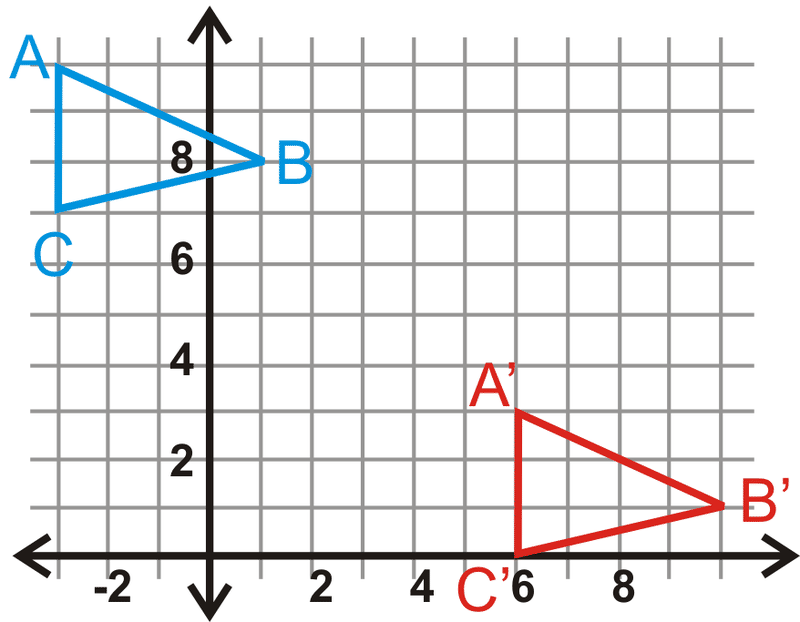
    Малюнок$\PageIndex{7}$

16. 

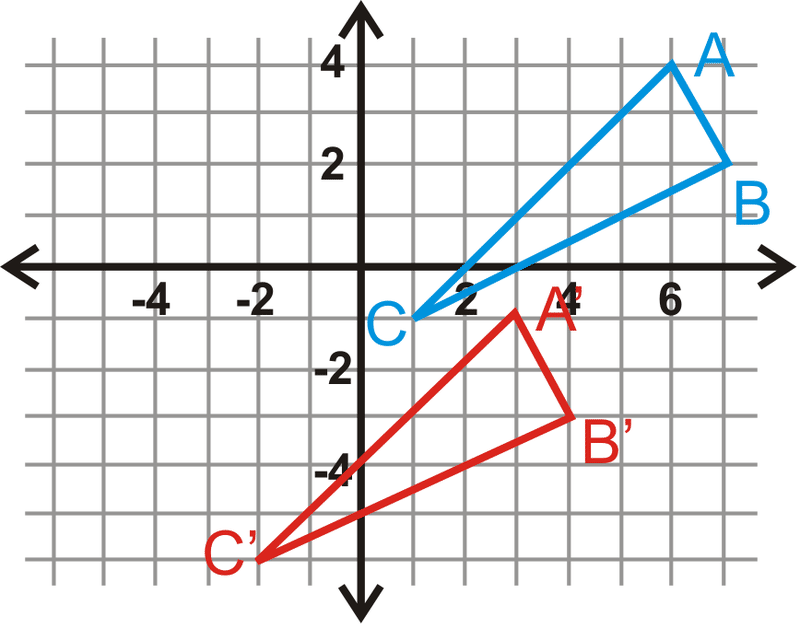
    Малюнок$\PageIndex{8}$

17. 

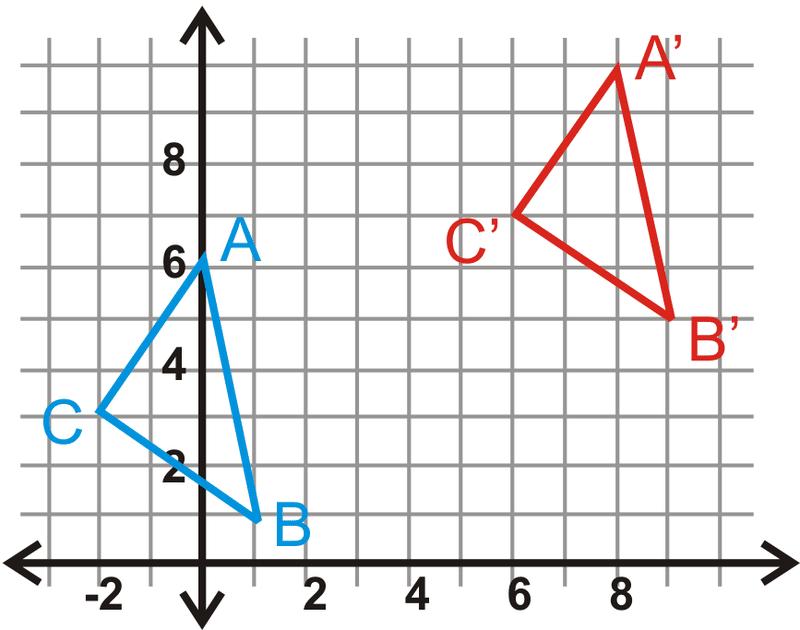
    Малюнок$\PageIndex{9}$

Використовуйте трикутники з #17, щоб відповісти на питання 18-20.

18. Знайдіть довжини всіх сторін$\Delta ABC$.
19. Знайдіть довжини всіх сторін$\Delta A′B′C′$.
20. Що можна сказати про$\Delta ABC$ і$\Delta A′B′C′$? Чи можете ви сказати це для будь-якого перекладу?
21. Якщо$\Delta A′B′C′$ був попереднім зображенням і$\Delta ABC$ був зображенням, напишіть правило перекладу для #14.
22. Якщо$\Delta A′B′C′$ був попереднім зображенням і$\Delta ABC$ був зображенням, напишіть правило перекладу для #15.
23. Знайдіть правило перекладу, до якого буде$A$ переходити$A′(0,0)$, для #16.
24. Координати$\Delta DEF$ є$D(4,−2)$,$E(7,−4)$ і$F(5,3)$. $\Delta DEF$Перевести вправо 5 одиниць і вгору 11 одиниць. Напишіть правило перекладу.
25. Координати чотирикутника$QUAD$ є$Q(−6,1)$,$U(−3,7)$,$A(4,−2)$ і$D(1,−8)$. Переведіть$QUAD$ вліво 3 одиниці і вниз 7 одиниць. Напишіть правило перекладу.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 12.3.

Додаткові ресурси

Інтерактивний елемент

Відео: Трансформація: Принципи перекладу - Основні

Види діяльності: Переклади Обговорення Питання

Навчальні посібники: Види трансформацій Навчальний посібник

Практика: Геометричний переклад