8.2: Лінії симетрії
- Page ID
- 54929
Визначте існування і кількість ліній симетрії.
Визначте лінії симетрії

Симетрія - запорука балансу конструкції або конструкції.
Що таке симетрія? Як зображення має симетрію? Що б вам довелося зробити, щоб бути впевненим, що зображення або конструкція були симетричними?
У цьому понятті ви навчитеся визначати лінії симетрії.
Симетрія
Іноді фігура матиме частини, які відображають себе в межах одного об'єкта. При цьому частини предмета збігаються з іншими частинами малюнка. Це називається симетрією.
Давайте розглянемо приклад.

Подивіться на це серце. Він має дві сторони, які збігаються. Серце симетричне, тому що в його дизайні присутня симетрія. Це серце можна розділити навпіл по вертикалі там, де одна половина збігається з іншою половиною.

Ця лінія, яка ділить серце на відповідні частини, називається лінією симетрії.
Ви можете визначити інші лінії симетрії, дивлячись на інші об'єкти.
Давайте розглянемо інший приклад.

Подивіться на цей хрест. Він має дві лінії симетрії. Якщо подивитися, то хрест можна розділити навпіл ідеально по вертикалі і навпіл по горизонталі.
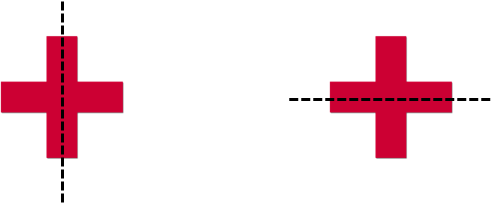
Це означає, що в хресті є дві лінії симетрії.
Приклад\(\PageIndex{1}\)
Раніше вам давали задачу про питання по симетрії.
- Що таке симетрія?
- Як зображення має симетрію?
- Що б вам довелося зробити, щоб бути впевненим, що ваш образ був симетричним?
Рішення
- Симетрія - це коли дві половини об'єкта збігаються. Іншими словами, ви можете розділити об'єкт на частини і частини конгруентні. Серце - це симетричний об'єкт, так само і буква А.
- Зображення має симетрію, оскільки його можна розділити навпіл так, щоб одна половина зображення відповідала іншій половині.
- Щоб зображення мало лінію симетрії, зображення повинно бути в змозі скласти одну лінію симетрії так, щоб дві частини були дзеркальним відображенням один одного. Складена лінія буде лінією симетрії. Зображення, яке є симетричним, матиме лінію симетрії, таку як квадрат (чотири лінії симетрії), коло (нескінченні лінії симетрії) або метелика (одна лінія симетрії).
Приклад\(\PageIndex{2}\)
Чи має ця фігура симетрія? Чи може це бути відображенням?

Рішення
Спочатку постарайтеся розділити цю метелика рівномірно, щоб одна сторона могла відображати іншу. Чи можете ви намалювати лінію симетрії?

Відповідь - так.
Тому має симетрію.
Приклад\(\PageIndex{3}\)
Чи має малюнок нижче симетрію? Чи може це бути відображенням?

Рішення
Спочатку постарайтеся розділити цю квітку рівномірно, щоб одна сторона могла відображати іншу. Чи можете ви намалювати лінію симетрії?

Відповідь - так.
Тому має симетрію.
Приклад\(\PageIndex{4}\)
Скільки ліній симетрії має ця фігура?

Рішення
Спочатку спробуйте розділити цей прямокутник рівномірно, щоб одна сторона могла відображати іншу. Чи можете ви намалювати лінію симетрії?

Відповідь - так. Тому прямокутник має дві лінії симетрії.
Приклад\(\PageIndex{5}\)
Чи мають ці фігури симетрію?

Рішення
Спочатку постарайтеся розділити ці зображення рівномірно, щоб одна сторона могла відображати іншу. Чи можете ви намалювати лінію симетрії для будь-якого з цих зображень?
Відповідь - ні.
Тому жоден з цих зображень не має лінії симетрії.
Рецензія
Використовуйте ілюстрацію, щоб відповісти на кожне питання.
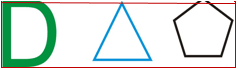
1. Чи мають ці фігури симетрію?
2. Чи можуть вони бути роздумами?
3. Скільки ліній симетрії має кожна фігура?
Знайдіть усі лінії симетрії для фігур нижче.
-
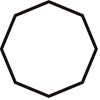
Малюнок\(\PageIndex{14}\) -

Малюнок\(\PageIndex{15}\) -
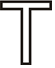
Малюнок\(\PageIndex{16}\)
Назвіть кількість рядків симетрії для кожної літери.
-

Малюнок\(\PageIndex{17}\) -

Малюнок\(\PageIndex{18}\) -

Малюнок\(\PageIndex{19}\) -

Малюнок\(\PageIndex{20}\) -

Малюнок\(\PageIndex{21}\)
Відповідь на кожне питання вірно або помилково.
12. Всі трикутники мають симетрію.
13. Всі кола мають симетрію.
14. Буква «\(x\)» має дві лінії симетрії.
15. Буква «\(s\)» має дві лінії симетрії.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 6.13.
Ресурси
Лексика
| Термін | Визначення |
|---|---|
| Лінії симетрії | Лінії симетрії - це лінії, які можна провести, щоб розділити фігуру на рівні половини. |
| Відображення | Відбиття - це перетворення, яке перевертає фігуру на координатній площині через задану лінію без зміни форми або розміру фігури. |
| Симетрія | Фігура має симетрію, якщо її можна перетворити і при цьому виглядати однаково. |
Додаткові ресурси
Відео: Підручник з обертальної симетрії
Практика: Лінії симетрії
Реальний світ: баланс природи