8.4: Симетрія обертання

Last updated

Oct 27, 2022
Save as PDF
- 8.3: Симетрія відображення
- 8.5: Геометричний переклад

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Обертання менше 360 градусів, що несе форму на себе.

Обертальна симетрія присутня, коли фігуру можна повертати (менше $360^{\circ}$ ) таким чином, щоб вона виглядала так, як це робилося до обертання. Центр обертання - це точка, навколо якої фігура обертається таким чином, щоб обертальна симетрія тримала.

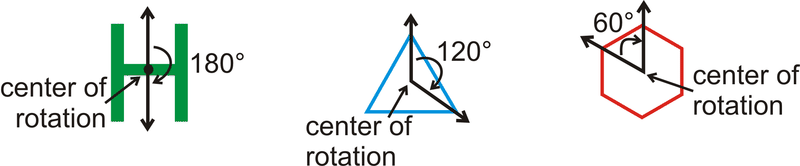
F-D_72ЕЕК 9820E716E5BE9C 494887549618 де 7Е2 ЕБД 3141ККА ЕБА 8Ф4А75+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Для $H$ , ми можемо повернути його двічі, трикутник можна повернути 3 рази і все ще виглядати однаково, а шестикутник можна повернути 6 разів.

Що робити, якщо у вас була шестикутна зірка і ви обертали цю зірку менше, ніж $360^{\circ}$ ? Якби повернута зірка виглядала точно так само, як оригінальна зірка, що б це говорило про зірку?

Приклад $\PageIndex{1}$

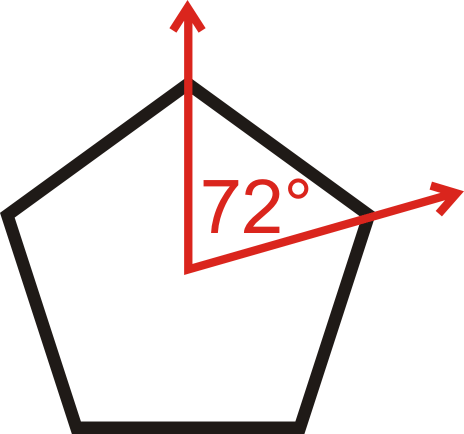
Визначте, чи має малюнок нижче обертальної симетрії. Знайдіть кут і скільки разів його можна повертати.

F-д_91а398Б6С92704Ф92АД 86д837ФБ0 ББ0 БББ 4А3487С94А973C766C939655C+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{2}$

Рішення

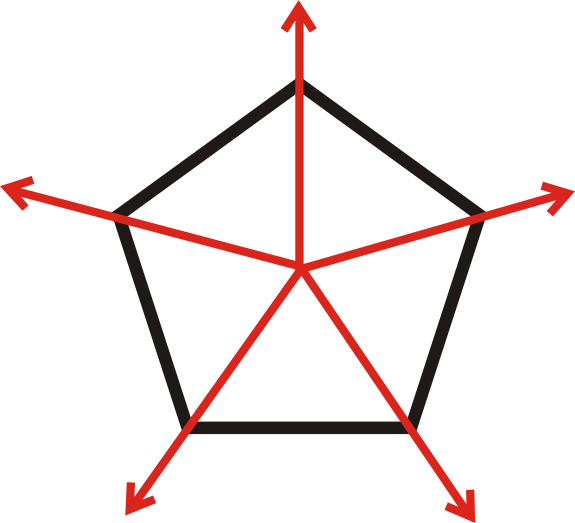
П'ятикутник можна обертати 5 разів. Оскільки є 5 ліній обертальної симетрії, кут буде $\dfrac{360^{\circ}}{5}=72^{\circ}$ .

F-D_593B85448 АД 28189ЕФ F9B47C1A4C1C148E385CC3690D23DC1+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

F-D_026D45D КАД 6А АБ 3Ф742Д1 ЕФ2ЕФ96Д68ЕЦ307755Ф4А4А42587854C7F7B+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{4}$

Приклад $\PageIndex{2}$

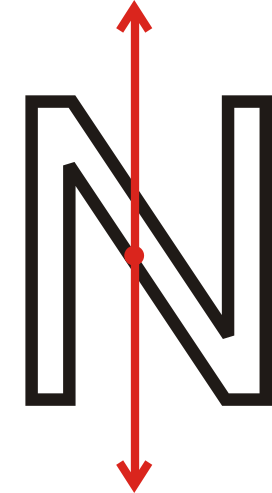
Визначте, чи має малюнок нижче обертальної симетрії. Знайдіть кут і скільки разів його можна повертати.

Ф-Д_445 ФД9Б29ДФ47Ф47АБ5 С4Д6КБ201ФД38Б1527Ф8Ф913405Д+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{5}$

Рішення

N можна повертати двічі. Це означає, що кут повороту є $180^{\circ}$ .

F-д_4С3Д08А3А3А6Б94Б94Б128Ф2Б32А584С097Б5705D626 AB472996D+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{6}$

Приклад $\PageIndex{3}$

Визначте, чи має малюнок нижче обертальної симетрії. Знайдіть кут і скільки разів його можна повертати.

F-D_80B 9928220553А93981 АЕ 6DC 2350Е96909Д8ДА0АА85АФА88365Б90Ф2+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{7}$

Рішення

Шахову дошку можна повертати 4 рази. Є 4 лінії обертальної симетрії, тому кут повороту дорівнює $\dfrac{360^{\circ}}{4}=90^{\circ}$ .

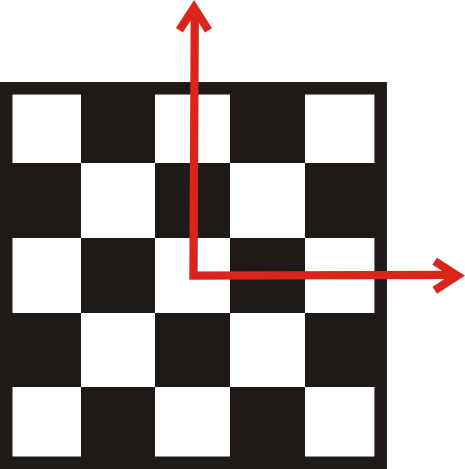
F-д_Ф8А2Б372815D48Ф2ББ2821Ф76С08АА6805С5Ф7Ф20313ECC22B2ФЕД+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{8}$

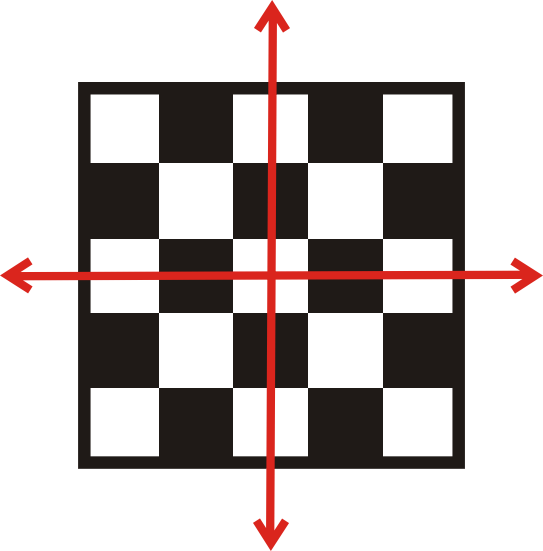
Ф-д_8С4Б0435Ф3С16Б1 ААФ 318 де 1С2Д1Ф159211С4ФКАФ 3ААЕ 8Ф1582Д6+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{9}$

Приклад $\PageIndex{4}$

Знайдіть кут повороту і кількість разів, коли кожна фігура може обертатися.

F-D_0D57550Б683С6Д5Е7 ЕФ 70А95ФД17АЕ 54С0Д5ЕЕ728Е36749А652E9+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{10}$

Рішення

Паралелограм можна повертати двічі. Кут повороту дорівнює $180^{\circ}$ .

Приклад $\PageIndex{5}$

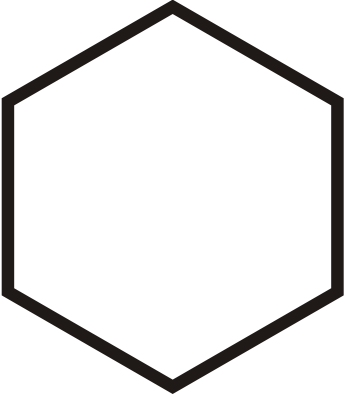
F-д_ЕД 3Б2Е99Е2970677Е5Б39Б1Д277613215Ф40ЕББС3Б64АЦ088D13+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{11}$

Рішення

Шестигранник можна обертати шість разів. Кут повороту дорівнює $60^{\circ}$ .

Рецензія

Якщо фігура має 3 лінії обертальної симетрії, її можна повертати _______ разів.
Якщо фігуру можна повернути 6 разів, вона має _______ ліній обертальної симетрії.
Якщо фігуру можна повернути n разів, вона має _______ ліній обертальної симетрії.
Щоб знайти кут повороту, ділимо $360^{\circ}$ на загальне число _____________.
Кожен квадрат має кут повороту _________.

Визначте, чи є кожне твердження істинним чи помилковим.

Кожен паралелограм має обертальну симетрію.
Кожна фігура, яка має симетрію лінії, також має обертальну симетрію.

Визначте, чи мають наведені нижче слова симетрію обертання.

ОГАЙО
КОСИТИ
WOW
УДАР
стручок

Знайдіть кут повороту і кількість разів, коли кожна фігура може обертатися.

Малюнок $\PageIndex{12}$
Малюнок $\PageIndex{13}$
Малюнок $\PageIndex{14}$

Визначте, чи мають наведені нижче цифри симетрію обертання. Визначте кут повороту.

Малюнок $\PageIndex{15}$
Малюнок $\PageIndex{16}$
Малюнок $\PageIndex{17}$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 12.2.

Лексика

Термін	Визначення
обертальна симетрія	Коли фігуру можна повертати (менше 360^ {\ circ}\)) так, щоб вона виглядала так, як це робилося до обертання. *Центр обертання* - це точка, навколо якої фігура обертається таким чином, щоб обертальна симетрія тримала.
Центр обертання	При обертанні центр обертання - це точка, яка не рухається. Інша частина площини обертається навколо цієї нерухомої точки.
Обертання	Обертання - це перетворення, яке перетворює фігуру на координатній площині на певну кількість градусів навколо заданої точки без зміни форми або розміру фігури.
Симетрія обертання	Фігура має обертальну симетрію, якщо її можна повернути менше, ніж $360^{\circ}$ навколо своєї центральної точки, і виглядати точно так само, як і до обертання.
Симетрія	Фігура має симетрію, якщо її можна перетворити і при цьому виглядати однаково.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи симетрії обертання - основні

Діяльність: Обертання Симетрія Дискусійні питання

Навчальні посібники: Посібник з вивчення симетрії та тесселяції

Практика: Симетрія обертання

Реальний світ: Це кінець