7.16: Розширення в координатній площині

Множення координат на масштабний коефіцієнт з урахуванням початку координат як центру.

Розширення в координатній площині

Дві фігури схожі, якщо вони однакової форми, але не обов'язково однакового розміру. Одним із способів створення подібних фігур є розширення. Розширення робить фігуру більшою або меншою, так що нове зображення має ту ж форму, що і оригінал.

Розширення: збільшення або зменшення фігури, яка зберігає форму, але не розмір. Всі розширення схожі на вихідну фігуру.

Розширення мають центр і масштабний коефіцієнт. Центр є точкою відліку для розширення, а масштабний коефіцієнт говорить нам, наскільки фігура розтягується або зменшується. Масштабний коефіцієнт позначається\(k\). Тільки позитивні масштабні фактори\(k\), будуть розглянуті в цьому тексті.

Якщо розширене зображення менше оригіналу, то\(0<k<1\).

Якщо розширене зображення більше оригіналу, то\(k>1\).

Щоб розширити щось у координатній площині, помножте кожну координату на коефіцієнт масштабу. Це називається картографуванням . Для будь-якого розширення картографування буде\((x,y)\rightarrow (kx,ky)\). У цьому тексті центром розширення завжди буде початок.

Що робити, якщо вам дали координати фігури і попросили розширити цю цифру на коефіцієнт масштабу 2? Як ви могли знайти координати розширеної фігури?

Для прикладів 1 і 2 скористайтеся наступною інструкцією:

Задано A і масштабний коефіцієнт, визначають координати розширеної точки,\(A′\). Ви можете припустити, що центром розширення є походження. Пам'ятайте, що відображення буде\((x, y)\rightarrow (kx, ky)\).

Приклад\(\PageIndex{1}\)

\(A(−4,6), k=2\)

Рішення

\(A′(−8,12)\)

Приклад\(\PageIndex{2}\)

\(A(9,−13), k=\dfrac{1}{2}\)

Рішення

\(A′(4.5,−6.5)\)

Приклад\(\PageIndex{3}\)

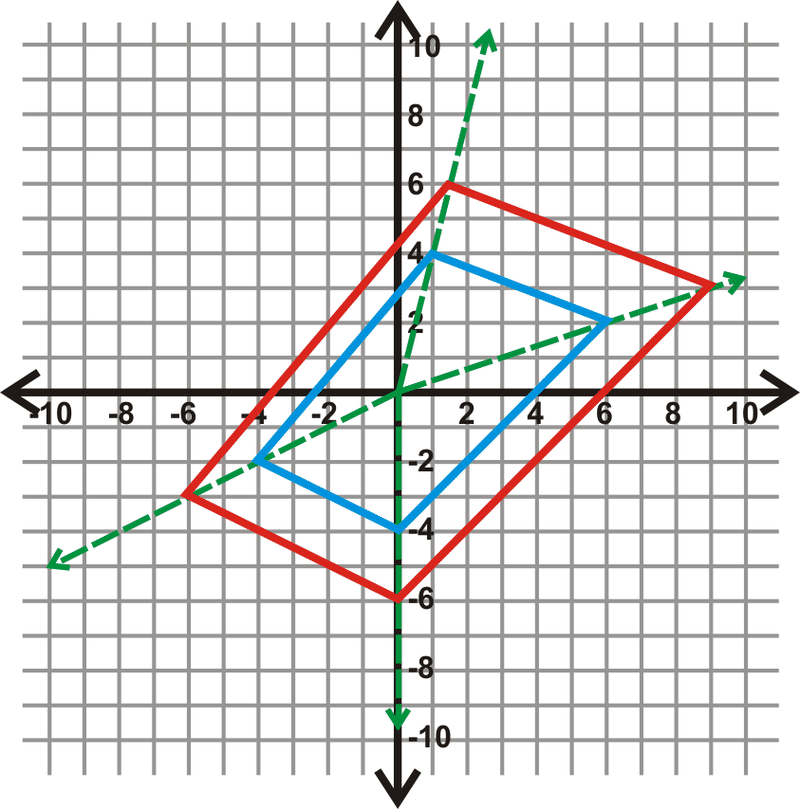
Чотирикутник EFGH\) має вершини\(E(−4,−2)\)\(F(1,4)\),\(G(6,2)\) і\(H(0,−4)\). Намалюйте дилатацію з масштабним коефіцієнтом 1,5.

Малюнок\(\PageIndex{1}\)

Рішення

Пам'ятайте, що для розширення чогось в координатній площині помножте кожну координату на коефіцієнт масштабу.

Для цього розширення відображенням буде\ (x, y)\ rightarrow (1.5x, 1.5y).

\(\begin{aligned} &E(−4,−2)\rightarrow (1.5(−4),1.5(−2))\rightarrow E′(−6,−3) \\ &F(1,4)\rightarrow (1.5(1),1.5(4))\rightarrow F′(1.5,6) \\ &G(6,2)\rightarrow (1.5(6),1.5(2))\rightarrow G′(9,3) \\ &H(0,−4)\rightarrow (1.5(0),1.5(−4))\rightarrow H′(0,−6)\end{aligned}\)

На графіку вище синій чотирикутник є оригіналом, а червоне зображення - розширення.

Приклад\(\PageIndex{4}\)

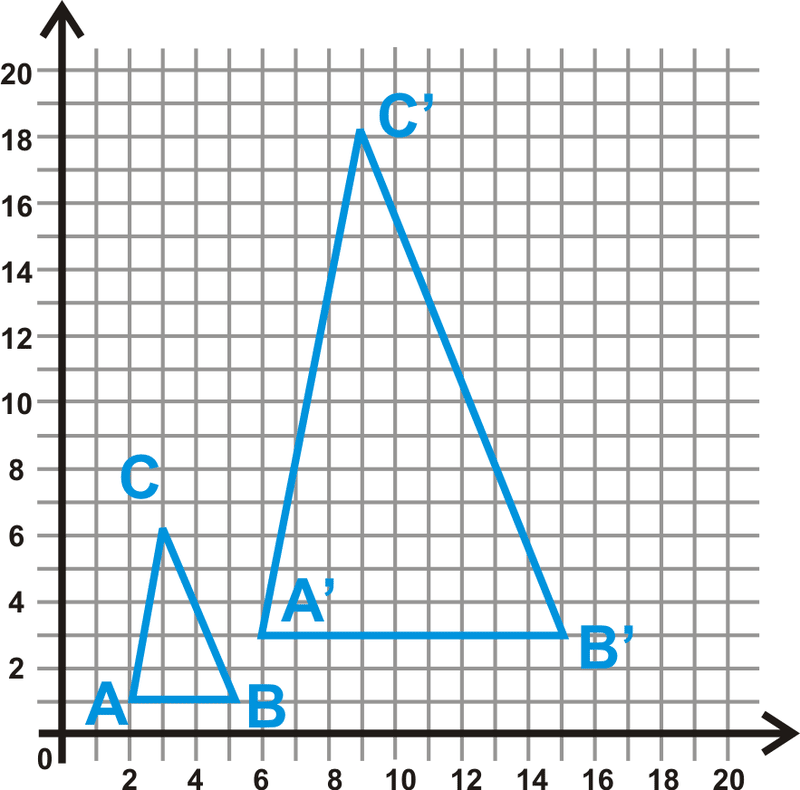
Визначте координати\(\Delta ABC\)\(\Delta A′B′C′\) і знайдіть масштабний коефіцієнт.

Малюнок\(\PageIndex{2}\)

Рішення

Координати вершин\(\Delta ABC\) є\(A(2,1)\), B (5,1)\) і C (3,6)\). Координати вершин\(\Delta A′B′C′\) є A′ (6,3)\)\(B′(15,3)\) і C′ (9,18)\). Кожна з відповідних координат втричі перевищує оригінал, так що\(k=3\).

Приклад\(\PageIndex{5}\)

Покажіть, що розширення зберігають форму за допомогою формули відстані. Знайдіть довжини сторін обох трикутників у прикладі B.

Рішення

\ (\ почати {масив} {ll}\ підкреслення {\ Дельта ABC} &\ підкреслення {\ Дельта A'B'C '}
A B =\ sqrt {(2-5) ^ {2} + (1-1) ^ {2}} =\ sqrt {9} =3 & A^ {\ прайм} B^ {\ прайм} =\ sqrt {(6-15) ^ {2} + (3-3) ^ {2}} =\ sqrt {81} =9\
A C=\ sqrt {(2-3) ^ {2} + (1-6) ^ {2}} =\ sqrt {26} & A^ {\ прайм} C^ {\ прайм} =\ sqrt {(6-9) ^ {2} + (3-18) ^ {2}} =3\ sqrt {26}\
C B=\ sqrt {(3-5) ^ {2} + (6-1) ^ {2}} =\ sqrt {29} & C^ {\ прайм} B^ {\ прайм} =\ sqrt {(9-15) ^ {2} + (18-3) ^ {2}} =3\ sqrt {29}
\ кінець {масив}\)

З цього ми також бачимо, що всі сторони в\(\Delta A′B′C′\) три рази більше, ніж\(\Delta ABC\).

Рецензія

Задано\(A\) і\(A′\), знайдіть масштабний коефіцієнт. Ви можете припустити, що центром розширення є походження.

1. \(A(8,2), A′(12,3)\)
2. \(A(−5,−9), A′(−45,−81)\)
3. \(A(22,−7), A(11,−3.5)\)

Походження - центр розширення. Намалюйте розширення кожної фігури, враховуючи масштабний коефіцієнт.

4. \(A(2,4), B(−3,7), C(−1,−2); k=3\)
5. \(A(12,8), B(−4,−16), C(0,10); k=34\)

Багатоступінчасті проблемні питання 6-9 будуються один на одному.

6. Ділянка\(A(1,2), B(12,4), C(10,10)\). З'єднайте, щоб сформувати трикутник.
7. Зробіть початок центром розширення. Намалюйте 4 промені від початку до кожної точки з #21. Потім, сюжет\(A′(2,4), B′(24,8), C′(20,20)\). Що таке масштабний коефіцієнт?
8. Використовуйте\(k=4\), щоб знайти\(A′′B′′C′′\). Побудуйте ці точки.
9. Що таке масштабний коефіцієнт від\(A′B′C′\) до\(A′′B′′C′′\)?

Якщо\(O\) це походження, знайдіть наступні довжини (використовуючи 6-9 вище). Округляйте всі відповіді до найближчих сотих.

10. \(OA\)
11. \(AA′\)
12. \(AA′′\)
13. \(OA′\)
14. \(OA′′\)
15. \(AB\)
16. \(A′B′\)
17. \(A′′B′′\)
18. Порівняйте співвідношення\(OA:OA′\) і\(AB: A′B′\). Що ви помічаєте? Чому ви думаєте, що це так?
19. Порівняйте співвідношення\(OA:OA′′\) і\(AB: A′′B′′\). Що ви помічаєте? Чому ви думаєте, що це так?

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 7.12.

Лексика

Термін	Визначення
Дилатація	Зменшити або збільшити цифру відповідно до масштабного коефіцієнта - це розширення.
Формула відстані	Відстань між двома точками\((x_1,y_1)\) і\((x_2,y_2)\) може бути визначено як\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\).
Картографування	Відображення - це процедура, яка передбачає побудову точок на координатній сітці, щоб побачити поведінку функції.
Масштабний коефіцієнт	Масштабний коефіцієнт - це відношення масштабу до вихідного або фактичного виміру, написаного в найпростішій формі.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи розширення в координатній площині - Основні

Діяльність: Розширення в координатній площині Дискусійні питання

Навчальні посібники: Види трансформацій Навчальний посібник

Практика: Розширення в координатній площині