Skip to main content
LibreTexts - Ukrayinska

7.7: Подібність AA

  1. Last updated
  2. Save as PDF
  • Page ID
    54626

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Два трикутника схожі, якщо дві пари кутів конгруентні.

    Постулат подібності AA

    За визначенням два трикутника схожі, якщо всі відповідні їм кути конгруентні, а відповідні їм сторони пропорційні. Не обов'язково перевіряти всі кути і сторони, щоб визначити, чи схожі два трикутника. Насправді, якщо ви знаєте лише, що дві пари відповідних кутів є конгруентними, достатньо інформації, щоб знати, що трикутники схожі. Це називається Постулатом подібності АА.

    Постулат подібності AA: Якщо два кути в одному трикутнику збігаються з двома кутами в іншому трикутнику, то два трикутника схожі.

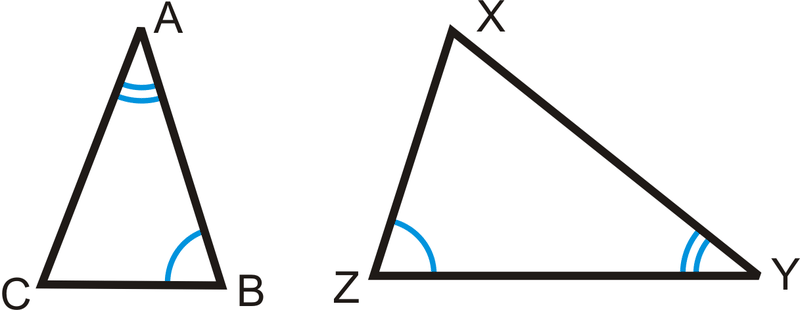
    F-д_5С0Б63785FF154E1ЕД постійного струму 4С52Б574Е558Ф2А4Е7Ф4Ф2Ф225146FCD67+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Якщо\(\angle A\cong \angle Y\) і\(\angle B\cong \angle Z\), то\(\Delta ABC\sim \Delta YZX\).

    Що робити, якщо вам дали пару трикутників і вимірювання кута для двох їх кутів? Як ви могли б використовувати цю інформацію, щоб визначити, чи два трикутники схожі?

    Приклад\(\PageIndex{1}\)

    Трикутники схожі? Якщо так, напишіть заяву подібності.

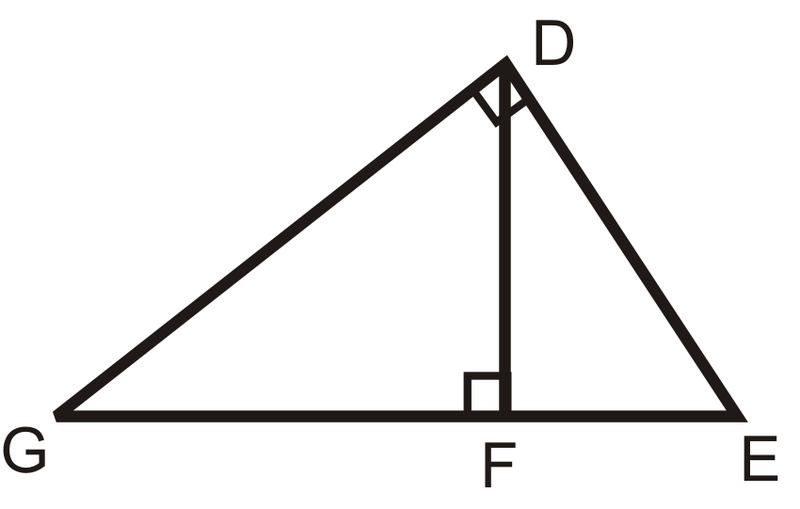
    Ф-д_А0Д8Ф73С36Е2Ф39Е821Е03876 АФ25ФБ8541635474С14660А5Е6Ф71Д+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Так, є три подібних трикутника, кожен з яких має прямий кут. \(DGE\sim FGD\sim FDE\).

    Приклад\(\PageIndex{2}\)

    Трикутники схожі? Якщо так, напишіть заяву подібності.

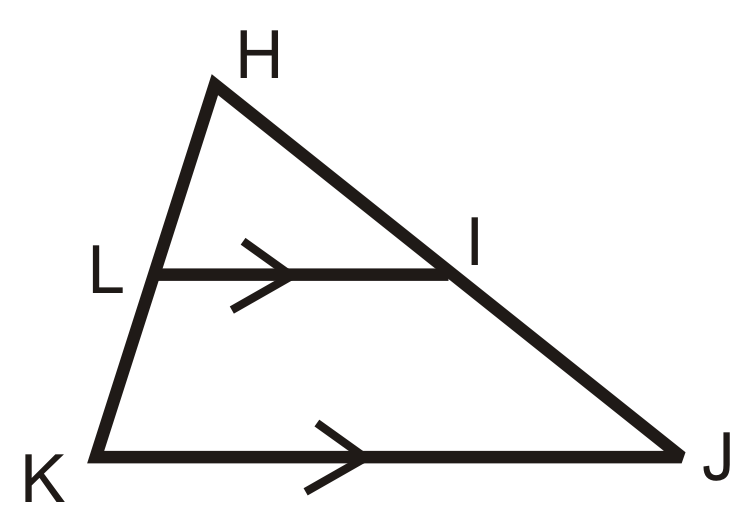
    F-D_E05ФД8АЕ759СА9ДАА9Б9Б151СБ124ФД242ДБ Б 4Ф9КД7Е3С00Д073+зображення_крихіткий+зображення_крихіткий_PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    За рефлексивним властивістю,\(\angle H\cong \angle H\). Тому що горизонтальні лінії паралельні,\(\angle L\cong \angle K\) (відповідні кути). Так що так, є пара подібних трикутників. \(HLI\sim HKJ\).

    Приклад\(\PageIndex{3}\)

    Визначте, чи схожі наступні два трикутника. Якщо так, напишіть заяву подібності.

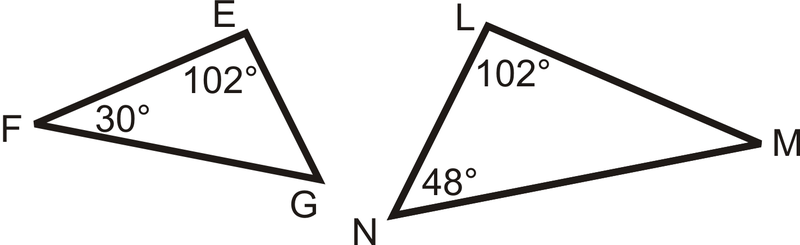
    F-д_Д0975А25АЕ10Ф6Д0 Беб 83Д83Б8 ЕЕ09Е789ЕБ805Ф31104А3Е91326+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Порівняйте кути, щоб побачити, чи можемо ми використовувати Постулат подібності AA. Використовуючи теорему про суму трикутника,\(m\angle G=48^{\circ}\) і\(m\angle M=30^{\circ}\). Отже\(\angle F\cong \angle M\),\(\angle E\cong \angle L\)\(\angle G\cong \angle N\) і трикутники схожі. \(\Delta FEG\sim \Delta MLN\).

    Приклад\(\PageIndex{4}\)

    Визначте, чи схожі наступні два трикутника. Якщо так, напишіть заяву подібності.

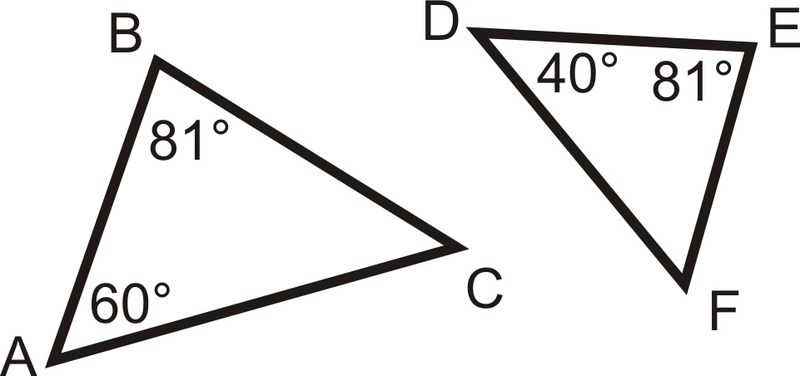
    F-D_C08299571 АБАФАДА 8 БДС53Д841Д9Ф 533811191Е794Д726Б43Б2А57Д0+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Порівняйте кути, щоб побачити, чи можемо ми використовувати Постулат подібності AA. Використовуючи теорему про суму трикутника,\(m\angle C=39^{\circ}\) і\(m\angle F=59^{\circ}\). \(m\angle C\neq m\angle F\), Так\(\Delta ABC\) і не\(\Delta DEF\) схожі.

    Приклад\(\PageIndex{5}\)

    \(\Delta LEG\sim \Delta MAR\)по А.А. Знайти\(GE\) і\(MR\).

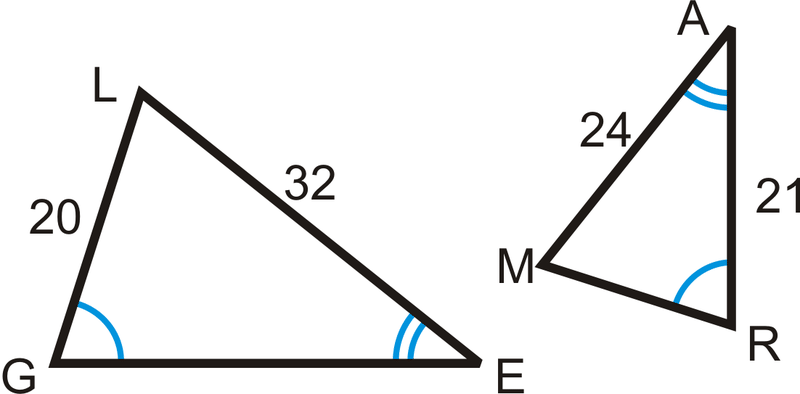
    Ф-Д_22С12Ф12Д44А4С4А536ДДД8КС23Б24 де 04607216 ЕСCD9C0FA84D187+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Налаштуйте пропорцію, щоб знайти відсутні сторони.

    \ (\ begin {масив} {rlrl}
    \ гідророзриву {24} {32} & =\ гідророзриву {M R} {20} &\ гідророзриву {24} {32} & =\ гідророзриву {21} {G E}\\
    480 & =32 M R & 24 G E & =672\\
    15 & =M R & G Е&=28
    \ кінець {масив}\)

    Коли два трикутника схожі, відповідні сторони пропорційні. Але, які відповідні сторони? Використовуючи трикутники з цього прикладу, ми бачимо, як сторони вишикуються на схемі праворуч.

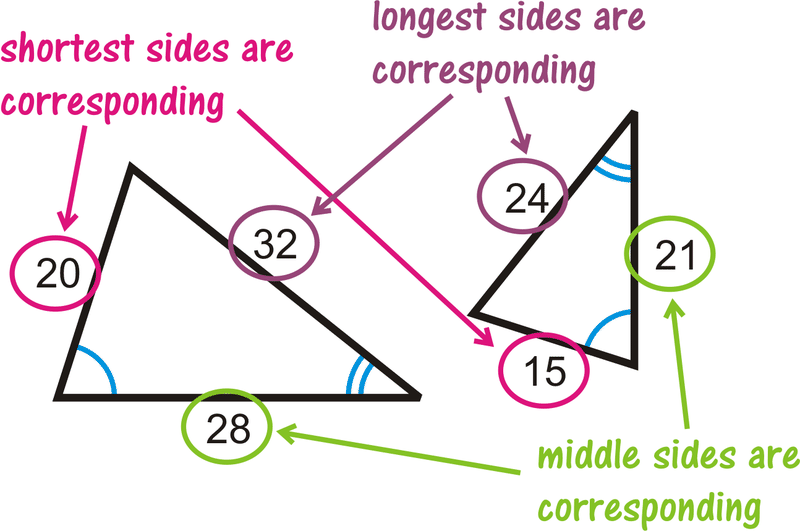
    F-D_32d8506BA8E6A0609BCE521109C0A1E80F31FA004A755F512FDBCD5B+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Рецензія

    Використовуйте діаграму, щоб завершити кожне твердження.

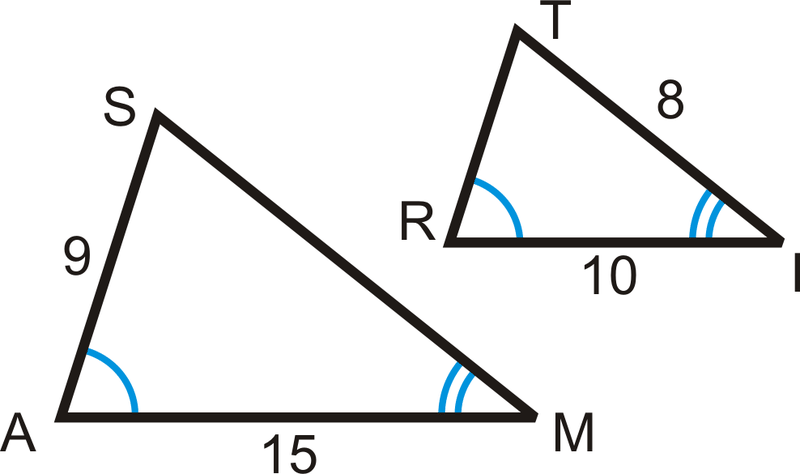
    Ф-Д_Б7337А 46 ККС14Б66ФА3109567CF774620 ЕФ697 БАЕ8АЕ72Б6485071E1E1+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)
    1. \(\Delta SAM\sim \Delta ______\)
    2. \(\dfrac{SA}{?}=\dfrac{SM}{?}=\dfrac{?}{RI}\)
    3. \(SM = ______\)
    4. \(TR = ______\)
    5. \(\dfrac{9}{?}=\dfrac{?}{8}\)

    Відповісти на питання 6-9 про трапеції\(ABCD\).

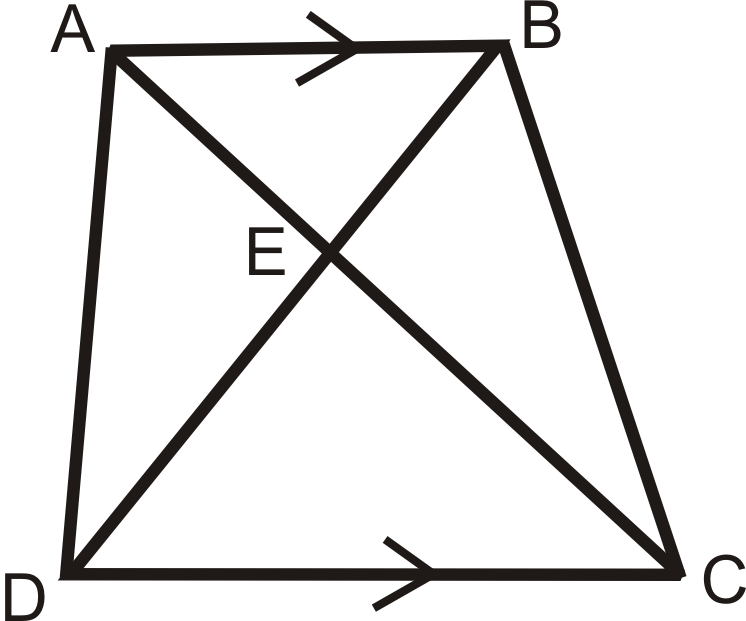
    F-D_07173Д10Е3А6ФА66С0ДАА 7771А325ФКА2023Ф8Б36Е93ААА5898А6+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)
    1. Назвіть два подібних трикутника. Звідки ви знаєте, що вони схожі?
    2. Напишіть справжню пропорцію.
    3. Назвіть два інших трикутника, які можуть бути не схожими.
    4. Якщо\(AB=10\)\(AE=7\), і\(DC=22\), знайти\(AC\). Будьте обережні!

    Використовуйте трикутники зліва для питань 10-14.

    \(AB=20\),\(DE=15\), і\(BC=k\).

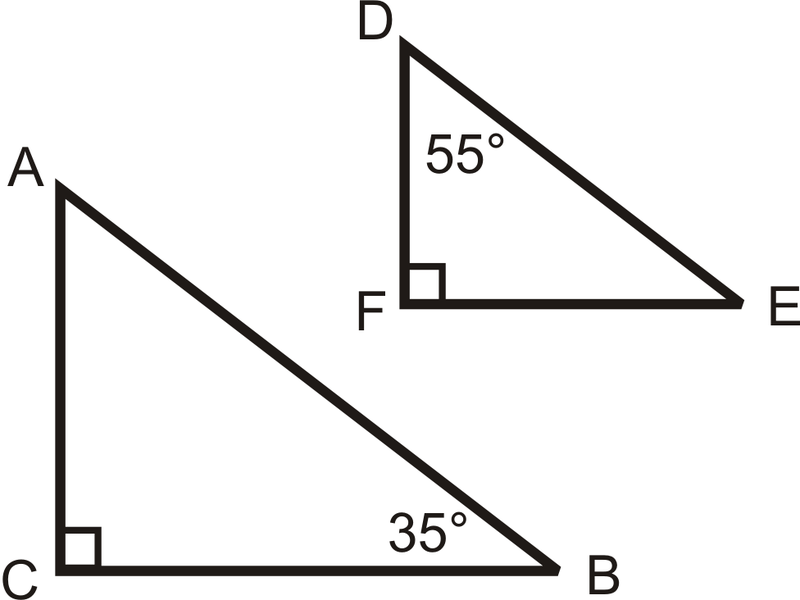
    F-D_941 АЦК 5Д 8Д 73Е9Д817С4459АА5А87Е334БФ ФБФ 288266FEC44FD822+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)
    1. Чи схожі два трикутника? Звідки ти знаєш?
    2. Напишіть вираз для з\(FE\) точки зору\(k\).
    3. Якщо\(FE=12\), що таке\(k\)?
    4. Заповніть пробіли: Якщо гострий кут _______ трикутника конгруентний гострому куту в іншому ________ трикутнику, то два трикутника - _______.
    5. Написання Як відрізняються конгруентні трикутники і подібні трикутники? Як вони однакові?

    Чи схожі наступні трикутники? Якщо так, напишіть заяву подібності.

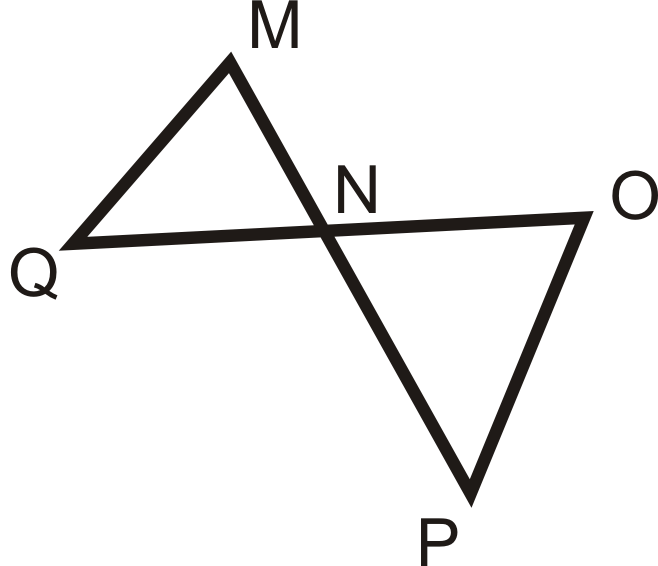
    1. Ф-Д_530004С598Е8ЕЕЕЕЕ6 АББ9 Ліжко 2А11Д3 Бе5Е4 Б3А02С560ЕС07ec4+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
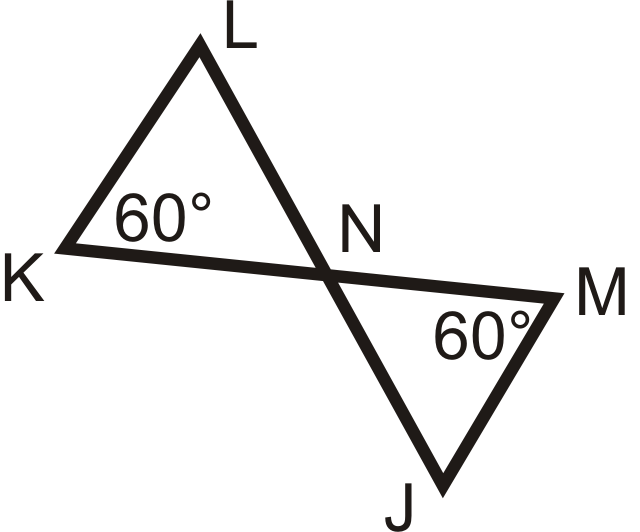
    2. F-D_79560D0ББД 243Ф22ФД559544Б1КД dae88 CDF5052959018A17EBD6CBF16+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
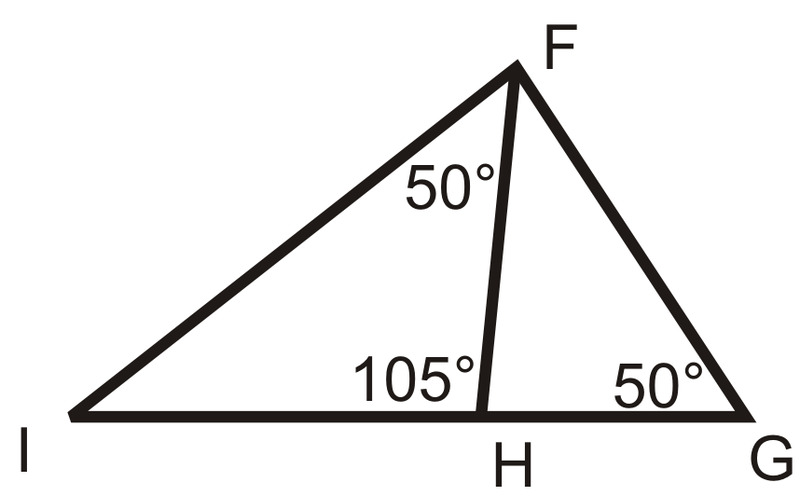
    3. F-д_Ф8 ЕД4Е94ДАД 844 ДБ55ЕЦ21Ф2АЕЕЕ95ЕД А0Б9Б4667ЕД5849Б+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
    4. F-д_Ф8 БАА 75122АББА 0А216А457Б4Д5Д92АБД 233Ф2БФДД 3762638E103623+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
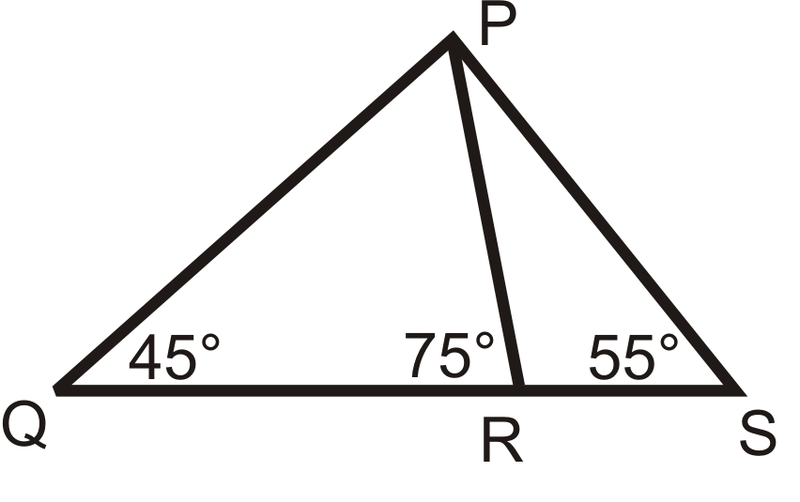
    5. F-D_64E8B2AE450DE1D8CCCD16F15DCF827A12ЕД 00157268714C3D6B1A40+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
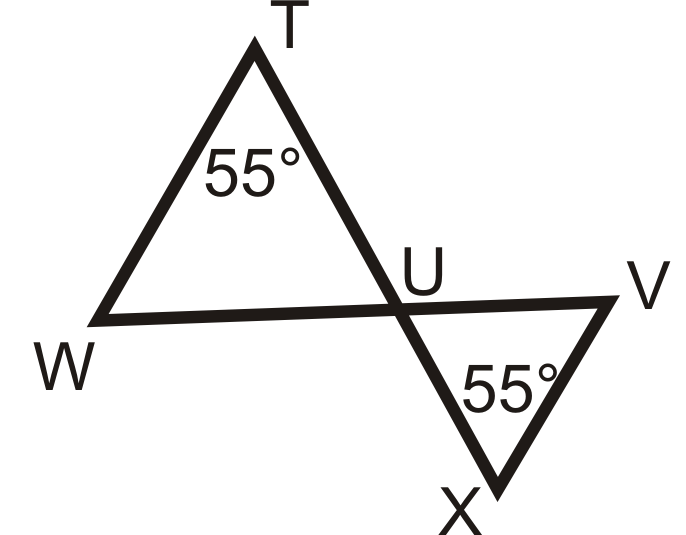
    6. F-D_4875045 ФБА 2АА15Б6Д807ФФ3 БК0А9 Плата 91C620 DeF8B3BDA23913834B+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
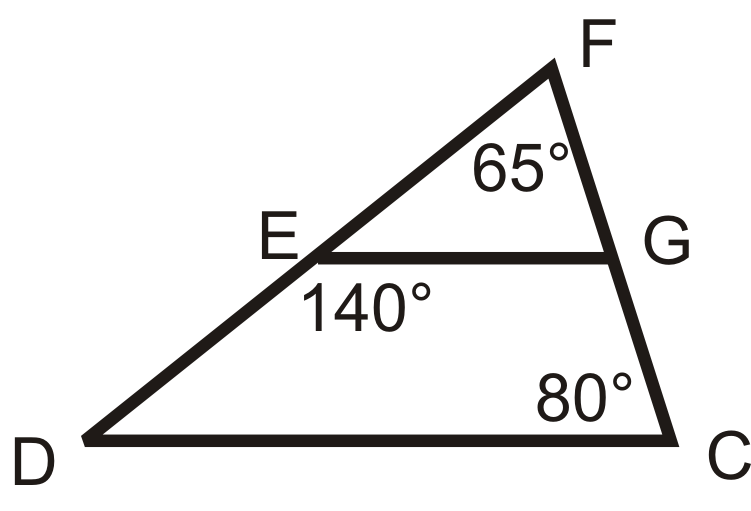
    7. F-д_4084 СА0711А179ФД8Ф3Ф8Ф3Ф89Д35Е77А9007С51FF1AFF4E4E4EB88A+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 7.4.

    Ресурси

    Лексика

    Термін Визначення
    подібні трикутники Два трикутника, де всі відповідні їм кути конгруентні (точно такі ж), а відповідні їм сторони пропорційні (в однаковому співвідношенні).
    Постулат подібності AA Якщо два кути в одному трикутнику конгруентні двом кутам в іншому трикутнику, то два трикутника схожі.
    Дилатація Зменшити або збільшити цифру відповідно до масштабного коефіцієнта - це розширення.
    Теорема про суму трикутника Теорема про суму трикутника стверджує, що три внутрішні кути будь-якого трикутника складають до 180 градусів.
    Жорстке перетворення Жорстке перетворення - це перетворення, яке зберігає відстань і кути, воно не змінює розмір або форму фігури.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Конгруентні та подібні трикутники

    Діяльність: Питання обговорення подібності AA

    Навчальні посібники: Посібник з вивчення схожості полі

    Практика: AA подібність

    Реальний світ: Божевільний ковдру