Skip to main content
LibreTexts - Ukrayinska

7.18: Самоподібність і фрактали

  1. Last updated
  2. Save as PDF
  • Page ID
    54609

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Одна частина об'єкта може бути збільшена або зменшена, щоб виглядати як весь об'єкт.

    Самоподібність

    Коли одна частина об'єкта може бути збільшена (або зменшена), щоб виглядати як весь об'єкт, вона схожа на себе.

    Щоб дослідити самоподібність, ми пройдемо кілька прикладів. Як правило, кожен крок процесу називається ітерацією . Перший рівень називається Stage 0 .

    Що робити, якщо вам дали такий предмет, як трикутник або сніжинка, в якому його частина могла бути збільшена (або зменшена), щоб виглядати як весь об'єкт? Як виглядатиме кожна наступна ітерація цього об'єкта?

    Приклад\(\PageIndex{1}\)

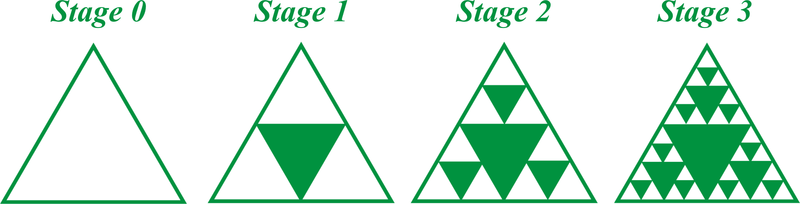
    Трикутник Серпінського повторює трикутник, з'єднуючи середні точки сторін і затінюючи центральний трикутник (Стадія 1). Повторіть цей процес для незатінених трикутників на етапі 1, щоб отримати етап 2.

    F-D_54498 1997 ФКБФ 4120Б476154 ДБ63КСД 52721 КД9935235СА1БА 3ФА2Б2+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Приклад\(\PageIndex{2}\)

    Визначте кількість затінених і незаштрихованих трикутників у кожному ступені трикутника Серпінського. Визначте, чи є закономірність.

    Етап 0 Етап 1 Етап 2 Етап 3
    Незатінений 1 3 9 27
    Затінений 0 1 4 13

    Рішення

    Кількість незатінених трикутників, здається, є степенями Кількість затінених трикутників - це сума кількості затінених і незаштрихованих трикутників з попереднього етапу.\(3:\: 3^{0},\: 3^{1},\: 3^{2},\: 3^{3},\: ….\) Наприклад, кількість затінених трикутників на етапі 4 дорівнюватиме\(27 + 13 = 40\).

    Приклад\(\PageIndex{3}\)

    Як і трикутник Сєрпінського, фрактал - це ще один самоподібний об'єкт, який повторюється в менших масштабах. Нижче наведені перші три етапи сніжинки Коха.

    F-д_Е89 БА 495ДФ 3277948 ДДБ0А92ДФБ462 ЕДДДД5Б6 ДДБ8ДБББ1585+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Приклад\(\PageIndex{4}\)

    Визначте кількість ребер і периметр кожної сніжинки, показані в прикладі 3. Припустимо, що довжина однієї сторони вихідного (етап 0) рівностороннього трикутника дорівнює 1.

    Етап 0 Етап 1 Етап 2
    Кількість ребер 3 12 48
    Довжина краю 1 \(\dfrac{1}{3}\) \(\dfrac{1}{9}\)
    Периметр 3 4 \(\dfrac{48}{9}=\dfrac{15}{3}\)

    Приклад\(\PageIndex{5}\)

    Набір Кантора - ще один приклад фракталу. Він складається з поділу сегмента на третини, а потім стирання середньої третини.

    F-д_9ФБ958Ф0528Д884Б2ДДДФ3Ф4Е89А5ББ7А5А639 АББ 9Е59Е024Ф801ДФ9Б+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рецензія

    1. Намалюйте 4 етап набору Кантора.
    2. Використовуйте Cantor Set, щоб заповнити таблицю нижче.
    Кількість сегментів Довжина кожного сегмента Загальна довжина сегментів
    Етап 0 1 1 1
    Етап 1 2 \(\dfrac{1}{3}\) \(\dfrac{2}{3}\)
    Етап 2 4 \(\dfrac{1}{9}\) \(\dfrac{4}{9}\)
    Етап 3
    Етап 4
    Етап 5
    1. Скільки сегментів у Stage\(n\)?
    2. Намалюйте 3 етап сніжинки Коха.
    3. Варіацією на трикутнику Сєрпінського є килим Серпінського, який розбиває квадрат на 9 рівних квадратів, розфарбовуючи тільки середній. Потім розділіть некольорові квадрати, щоб отримати наступний етап. Намалюйте перші 3 етапи цього фракталу.
    4. Скільки кольорових та некольорових квадратів на кожному етапі?
    5. Фрактали дуже поширені в природі. Наприклад, лист папороті - фрактал. У міру наближення листя до кінця вони стають все менше і менше. Знайдіть три інших приклади фракталів в природі.
    F-D_A3E71883 ДФ 558 CF8БФ 97594КА7А346Д82АБ 1С6 ЕЦБ79Д6Б66Е742+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 7.13.

    Лексика

    Термін Визначення
    самоподібний Коли одна частина об'єкта може бути збільшена (або скорочена), щоб виглядати як весь об'єкт.
    Ітерація Ітерація - це один крок у процесі.
    середина Середина відрізка лінії - це точка на відрізку лінії, яка розділяє відрізок на дві конгруентні частини.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Приклади самоподібності - основні

    Діяльність: Самоподібність Дискусійні питання

    Навчальні посібники: Посібник з вивчення подібності

    Практика: Самоподібність і фрактали

    Реальний світ: Фрактали скрізь