7.17: Розширення картографування
- Page ID
- 54707
Фігури, які можуть бути перенесені один до одного за допомогою одного або декількох жорстких перетворень з подальшим розширенням. Правила, що описують задані зміни розміру зображень
Правила для розширення
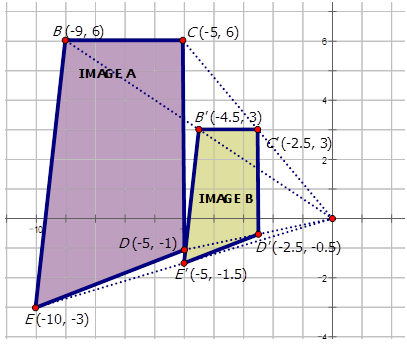
На малюнку нижче показано розширення двох трапецій. Запишіть правило відображення для розширення зображення A до зображення B.
У геометрії трансформація - це операція, яка переміщує, перевертає або змінює фігуру для створення нової форми. Розширення - це тип перетворення, який збільшує або зменшує фігуру (називається попереднім зображенням) для створення нової фігури (званої зображенням). Масштабний коефіцієнт визначає\(r\), наскільки більшим або меншим буде порівнюватися зображення розширення з попереднім зображенням.
Подивіться на схему нижче:
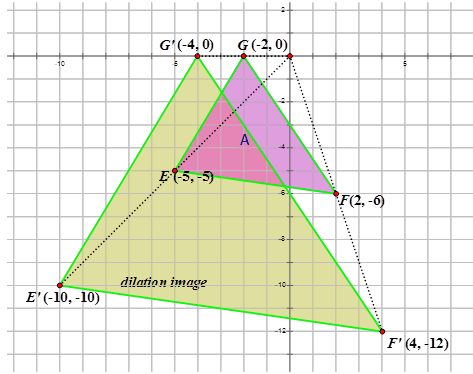
Зображення А зазнало розширення щодо походження з коефіцієнтом масштабу 2. Зверніть увагу, що точки на зображенні розширення подвоюють координатні точки на попередньому зображенні. Розширення з масштабним\(k\) коефіцієнтом про походження можна описати за допомогою наступних позначень:
\(D_{k} (x,y)=(kx,ky)\)
\(k\)завжди буде значенням, яке більше 0.
| Коефіцієнт масштабування, к | Зміна розміру для попереднього зображення |
|---|---|
| \(k>1\) | Зображення розширення більше, ніж попереднє зображення |
| \(0<k<1\) | Зображення розширення менше, ніж попереднє зображення |
| \(k=1\) |
Зображення розширення має той самий розмір, що і зображення попереднього зображення |
Давайте намалюємо зображення розширення для наступних відображень:
- Правило відображення для розширення, застосованого до трикутника нижче, є\((x,y)\rightarrow (1.5x,1.5y)\).
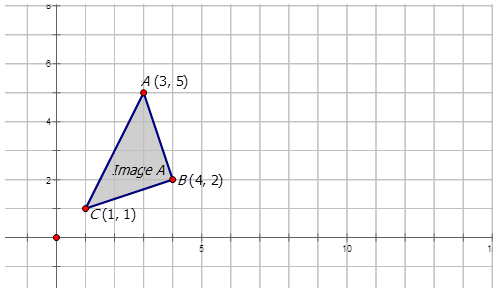
При масштабному коефіцієнті 1,5 кожна точка координат буде множитися на 1,5.
\ (\ begin {масив} {llcc}
\ текст {зображення} A & A (3,5) & B (4,2) & C (1,1)\
\ текст {Розширення зображення} & A^ {\ prime} (4.5,7.5) & B^ {\ prime} (6,3) & C ^ {\ прайм} (1.5,1.5)
\ кінець {масив}\)
Зображення розширення виглядає наступним чином:
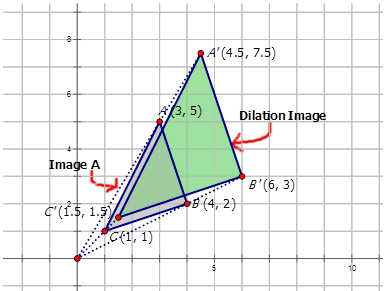
- Правило відображення для розширення, застосоване до наведеної нижче діаграми, є\((x,y)\rightarrow (\dfrac{1}{3}x, \dfrac{1}{3}y)\).
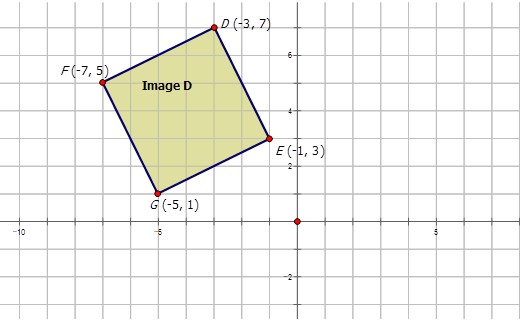
При масштабному коефіцієнті\(\dfrac{1}{3}\) кожна точка координат буде помножена на\(\dfrac{1}{3}\).
\ (\ begin {масив} {lllr}
\ текст {зображення} D & D (-3,7) & E (-1,3) & F (-7,5) & G (-5,1)\
\ текст {зображення розширення} & D^ {\ prime} (-1,2.3) & E^ {\ прайм} (-0.3,1) & F^ {\ prime} (-2.3,1.7) & G^ {\ прайм} (-1.7,0.3)
\ end {масив}\)
Зображення розширення виглядає наступним чином:
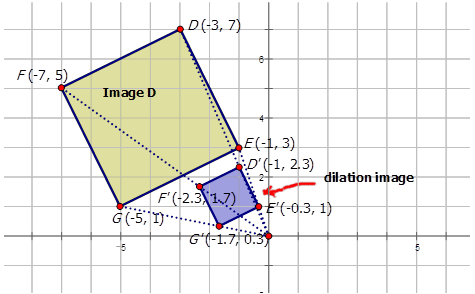
Тепер давайте напишемо позначення, яке представляє розширення попереднього зображення A до зображення розширення J на діаграмі нижче:
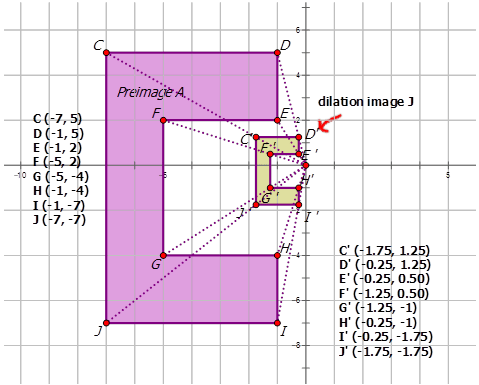
Спочатку виберіть точку на діаграмі, щоб побачити, як на неї вплинуло розширення.
\(C:(−7,5)\qquad C′:(−1.75,1.25)\)
Зверніть увагу, як обидва x- і y-координати множаться на\(\dfrac{1}{4}\). Це вказує на те, що попереднє зображення\(A\) зазнає розширення щодо походження за допомогою масштабного коефіцієнта,\(\dfrac{1}{4}\) щоб сформувати зображення розширення\(J\). Тому позначення відображення є\((x,y)\rightarrow (\dfrac{1}{4}x,\dfrac{1}{4}y)\).
Приклад\(\PageIndex{1}\)
Раніше вам було запропоновано написати правило відображення для розширення зображення A до зображення B на зображенні нижче:

Рішення
Подивіться на точки на кожному зображенні:
\ (\ begin {масив} {lllll}
\ текст {зображення} A & B (-9,6) & C (-5,6) & D (-5, -1) & E (-10, -3)\
\ текст {зображення} B & B ^ {\ прайм} (-4.5,3) & C ^ {\ прайм} (-2.5,3) & D^ {\ прайм} (-2.5, -0.5) & E^ {\ прайм} (-5, -1.5)
\ end {масив}\)
Зверніть увагу, що координатними точками зображення B (зображення розширення) є\ dfrac {1} {2}\), які знайдені на зображенні A\). Тому зображення A зазнає розширення щодо походження масштабного фактора\ dfrac {1} {2}\). Щоб написати правило відображення для цього розширення, ви повинні написати: (x, y)\ rightarrow (\ dfrac {1} {2} x,\ dfrac {1} {2} y)\).
Приклад\(\PageIndex{2}\)
Томас описує розширення точки\(JT\) з вершинами\(J(−2,6)\)\(T(6,2)\) до точки\(J′T′\) з вершинами\(J′(−4,12)\) і\(T′(12,4)\). Напишіть позначення, щоб описати це розширення для Томаса.
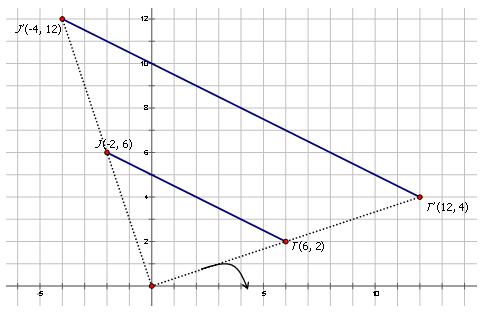
Рішення
Оскільки координати x і y множаться на 2, коефіцієнт масштабу дорівнює 2. Позначення відображення є:\((x,y)\rightarrow (2x,2y)\)
Приклад\(\PageIndex{3}\)
Враховуючи точки\(A(12,8)\) і\(B(8,4)\) на лінії, яка проходить розширення, щоб виробити\(A′(6,4)\) і\(B′(4,2)\), напишіть позначення, що представляє розширення.
Рішення
Для того, щоб написати позначення для опису розширення, виберіть одну точку на попередньому зображенні, а потім відповідну точку на зображенні розширення, щоб побачити, як точка перемістилася. Зверніть увагу, що точка EA\):
\(A(12,8)\rightarrow A′(6,4)\)
Оскільки обидва x- і y-координати множаться на\(\dfrac{1}{2}\), розширення приблизно походження має масштабний коефіцієнт\(\dfrac{1}{2}\). Позначення для цього розширення було б:\((x,y)\rightarrow (\dfrac{1}{2}x,\dfrac{1}{2}y)\).
Приклад\(\PageIndex{4}\)
Джанет грала з програмою малювання на своєму комп'ютері. Вона створила наступні діаграми, а потім хотіла визначити перетворення. Напишіть правило позначення, яке представляє перетворення фіолетової та синьої діаграми на помаранчеву та синю діаграму.
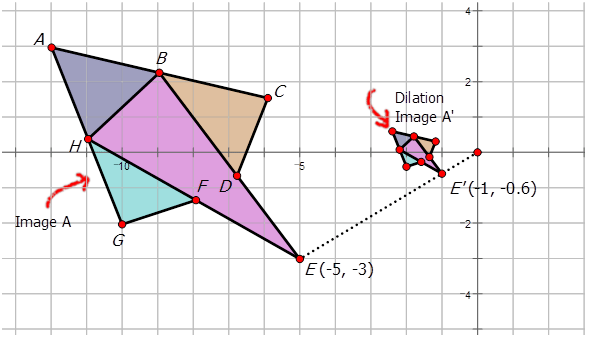
Рішення
Для того, щоб написати позначення для опису розширення, виберіть одну точку на попередньому зображенні,\(A\) а потім відповідну точку на зображенні розширення,\(A′\) щоб побачити, як змінилася точка. Зверніть увагу, що точка\(E\) показана на схемі:
\(E(−5,−3)\rightarrow E′(−1,−0.6)\)
Оскільки обидва x- і y-координати множаться на\(\dfrac{1}{5}\), розширення приблизно походження має масштабний коефіцієнт\(\dfrac{1}{5}\). Позначення для цього розширення було б:\((x,y)\rightarrow (\dfrac{1}{5}x, \dfrac{1}{5}y)\).
Рецензія
Заповніть наступну таблицю. Припустимо, що центром розширення є походження.
| Початкова точка | \(D_{2}\) | \(D_{5}\) | \(D_{\dfrac{1}{2}}\) | \(D_{\dfrac{3}{4}}\) |
|---|---|---|---|---|
| 1. (1, 4) | \ (D_ {2}\)» клас = "lt-k12-5951"> | \ (D_ {5}\)» клас = "lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)» клас ="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)» клас ="lt-k12-5951"> |
| 2. (4, 2) | \ (D_ {2}\)» клас = "lt-k12-5951"> | \ (D_ {5}\)» клас = "lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)» клас ="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)» клас ="lt-k12-5951"> |
| 3. (2, 0) | \ (D_ {2}\)» клас = "lt-k12-5951"> | \ (D_ {5}\)» клас = "lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)» клас ="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)» клас ="lt-k12-5951"> |
| 4. (-1, 2) | \ (D_ {2}\)» клас = "lt-k12-5951"> | \ (D_ {5}\)» клас = "lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)» клас ="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)» клас ="lt-k12-5951"> |
| 5. (-2, -3) | \ (D_ {2}\)» клас = "lt-k12-5951"> | \ (D_ {5}\)» клас = "lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)» клас ="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)» клас ="lt-k12-5951"> |
| 6. (9, 4) | \ (D_ {2}\)» клас = "lt-k12-5951"> | \ (D_ {5}\)» клас = "lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)» клас ="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)» клас ="lt-k12-5951"> |
| 7. (-1, 3) | \ (D_ {2}\)» клас = "lt-k12-5951"> | \ (D_ {5}\)» клас = "lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)» клас ="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)» клас ="lt-k12-5951"> |
| 8. (-5, 2) | \ (D_ {2}\)» клас = "lt-k12-5951"> | \ (D_ {5}\)» клас = "lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)» клас ="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)» клас ="lt-k12-5951"> |
| 9. (2, 6) | \ (D_ {2}\)» клас = "lt-k12-5951"> | \ (D_ {5}\)» клас = "lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)» клас ="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)» клас ="lt-k12-5951"> |
| 10. (-5, 7) | \ (D_ {2}\)» клас = "lt-k12-5951"> | \ (D_ {5}\)» клас = "lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)» клас ="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)» клас ="lt-k12-5951"> |
Напишіть позначення, яке представляє розширення попереднього зображення до зображення для кожної діаграми нижче.
-
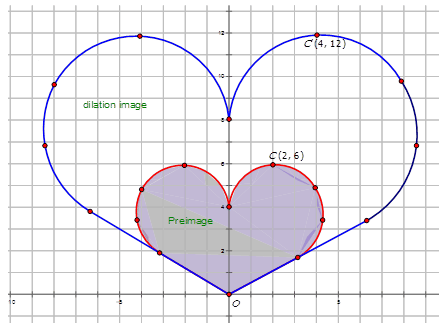
Малюнок\(\PageIndex{11}\) -
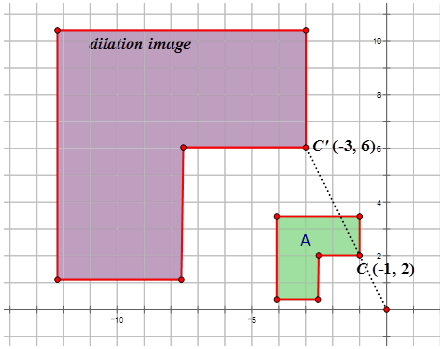
Малюнок\(\PageIndex{12}\) -
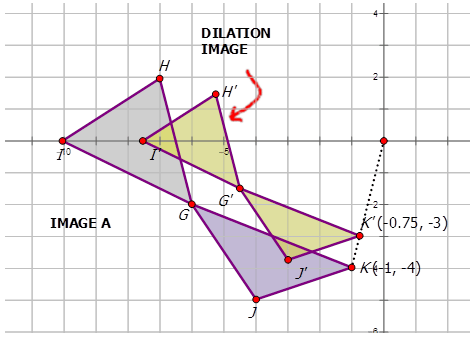
Малюнок\(\PageIndex{13}\) -
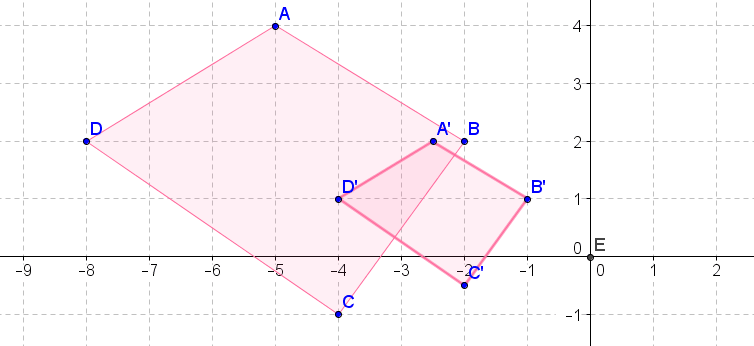
Малюнок\(\PageIndex{14}\) -
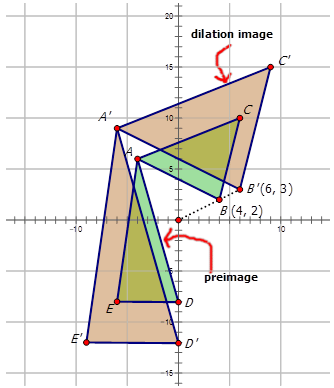
Малюнок\(\PageIndex{15}\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 10.12.
Додаткові ресурси
Інтерактивний елемент
Відео: SAT Math (Геометрія) - Практика 2.7
Практика: Картування дилатацій