7.15: Розширення форми

Last updated
Save as PDF

Page ID: 54695

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Більший або зменшений варіант фігури, що зберігає свою форму.

Дилатація

Дві фігури схожі, якщо вони однакової форми, але не обов'язково однакового розміру. Одним із способів створення подібних фігур є розширення. Розширення робить фігуру більшою або меншою, але нова отримана фігура має ту ж форму, що і оригінал.

Розширення: збільшення або зменшення фігури, яка зберігає форму, але не розмір. Всі розширення схожі на вихідну фігуру.

Розширення мають центр і масштабний коефіцієнт. Центр є точкою відліку для розширення, а масштабний коефіцієнт говорить нам, наскільки фігура розтягується або зменшується. Масштабний коефіцієнт позначається\(k\). Тільки позитивні масштабні фактори\(k\), будуть розглянуті в цьому тексті.

Якщо розширене зображення менше оригіналу, то\(0<k<1\).

Якщо розширене зображення більше оригіналу, то\(k>1\).

За розширенням, або зображенням, завжди слідує a\(′\).

*Позначте це*	*Скажи це*
\(′\)	«прайм» (копія оригіналу)
\(A′\)	«прайм» (копія точки\(A\))
\(A′′\)	«подвійний прайм» (другий примірник)

Що робити, якщо ви збільшили або зменшили трикутник, не змінюючи його форми? Як ви могли знайти масштабний коефіцієнт, за допомогою якого трикутник був розтягнутий або скорочений?

Приклад\(\PageIndex{1}\)

Знайдіть периметри\(KLMN\) і\(K′L′M′N′\). Порівняйте це співвідношення з коефіцієнтом масштабування.

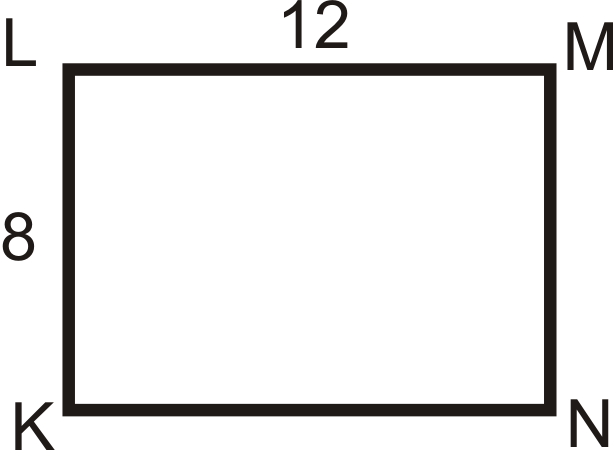
F-D_F0C1594C2 ББББ 61С374БА 5С3748Ф8Б381 САД830Б33ЕД 6Е181Ф953Б74Ф+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Рішення

По периметру\(KLMN=12+8+12+8=40\). По периметру\(K′L′M′N′=24+16+24+16=80\). Співвідношення становить 80:40, що зменшується до 2:1, що те саме, що і коефіцієнт масштабування.

Приклад\(\PageIndex{2}\)

F-д_2709ад03596 ЕЕ418429052Б007Д7Д7Е83СА7А7АЦ308D93121F5B8770AE1+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

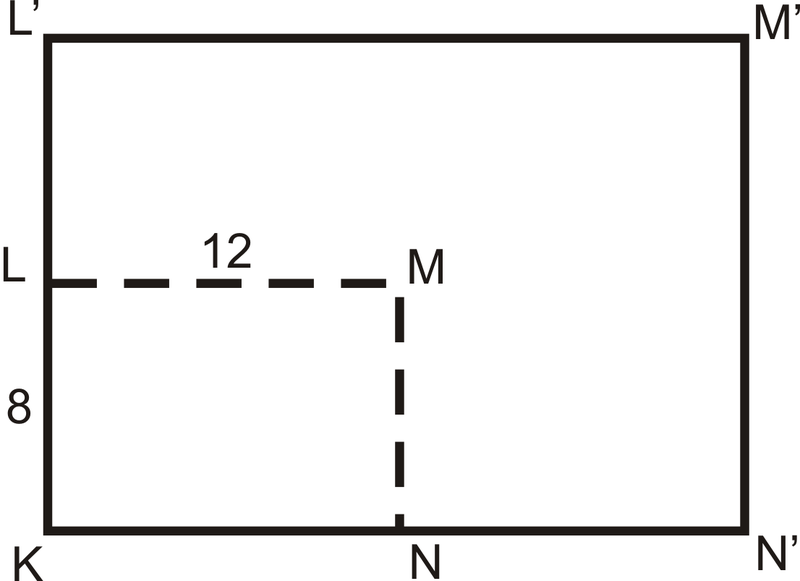
\(\Delta ABC\)є розширенням\(\Delta DEF\). Якщо P - центр розширення, що таке масштабний коефіцієнт?

Рішення

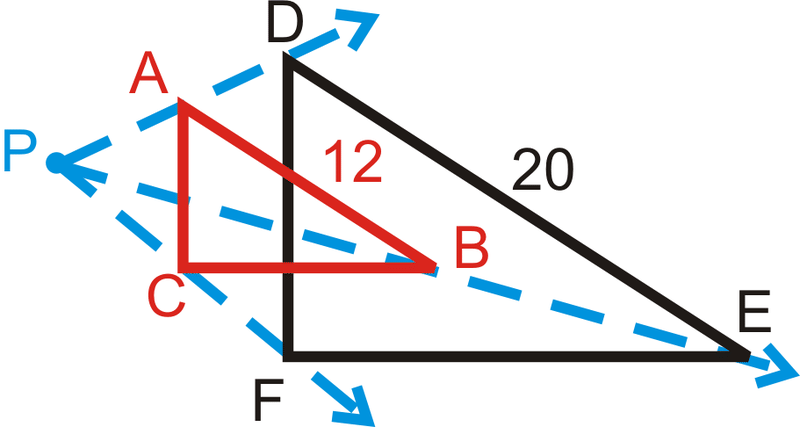
F-D_570c7109D64E5751 CFD19 БД28Ф8594Б0А9Б819ЕФ9А85К0Ф9Ф9Ф9Ф9Ф9Ф9Ф983Дака+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Тому що\(\Delta ABC\) це розширення\(\Delta DEF\), то\(\Delta ABC\sim \Delta DEF\). Масштабний коефіцієнт - це співвідношення сторін. Оскільки\(\Delta ABC\) він менший, ніж оригінал\(\Delta DEF\), коефіцієнт масштабування буде менше одиниці\(\dfrac{12}{20}=\dfrac{3}{5}\).

Якби\(\Delta DEF\) було розширене зображення, коефіцієнт масштабу був би\(\dfrac{5}{3}\).

Приклад\(\PageIndex{3}\)

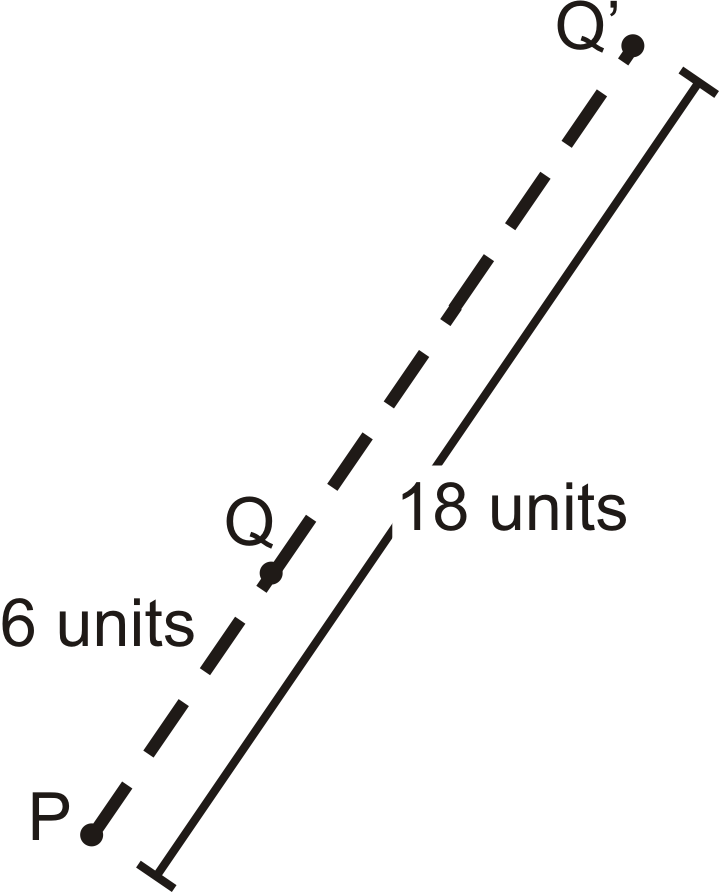
Центр розширення є,\(P\) а масштабний коефіцієнт дорівнює 3.

Знайти\(Q′\).

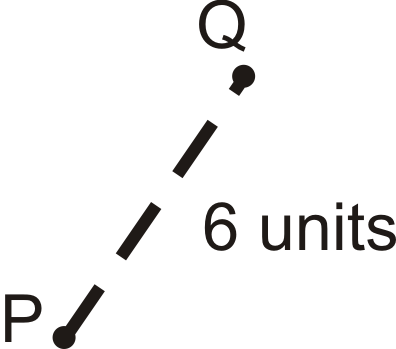
Ф-д_394ФББ 3Ф6Ф9 КФФФ 1510Д015488 ФЕ115А16Е0345 ББ09483Д Зникає+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Рішення

Якщо коефіцієнт масштабу дорівнює 3 і\(Q\) знаходиться на відстані 6 одиниць\(P\),\(Q′\) то буде\(6\times 3=18\) одиниць далеко від\(P\). Розширене зображення буде знаходитися на тій самій лінії, що і вихідне зображення і центр.

F-д_38Б563 ДК 51Е584А7АФ 5С32142Б6А9 Дед 9А7А9Е3Д5ДББДБ2А693+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Приклад\(\PageIndex{4}\)

Використовуючи малюнок вище, змініть масштабний коефіцієнт на 13.

Знайдіть,\(Q′′\) використовуючи цей новий масштабний коефіцієнт.

Рішення

Масштабний коефіцієнт\(Q′′\) є\(\dfrac{1}{3}\), так буде\(6\times \dfrac{1}{3}=2\) одиниць далеко від\(P\). \(Q′′\)також буде колінеарним з\(Q\) і центром.

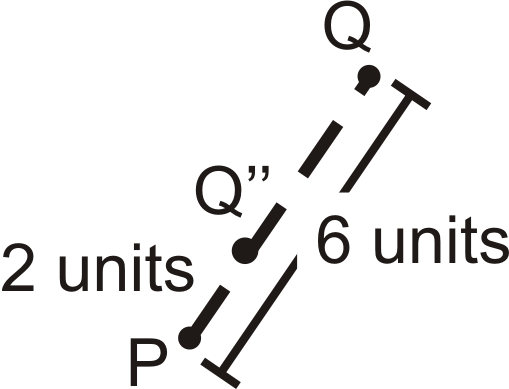
Ф-Д_4Е1487А277Ф9БК9БК945С85Ф6А2ББ 46034Ф63Б80376498Ф10С768А94Б+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Приклад\(\PageIndex{5}\)

\(KLMN\)являє собою прямокутник. Якщо центр розширення -\(K\) і\(k=2\), намалюйте\(K′L′M′N′\).

Рішення

Якщо\(K\) це центр розширення, то\(K\) і\(K′\) буде такою ж точкою. Звідти,\(L′\) буде 8 одиниць вище\(L\) і\(N′\) буде 12 одиниць праворуч від\(N\).

Рецензія

Для заданих фігур намалюйте розширення, враховуючи масштабний коефіцієнт і центр.

\(k=3.5\), центр є\(A\)

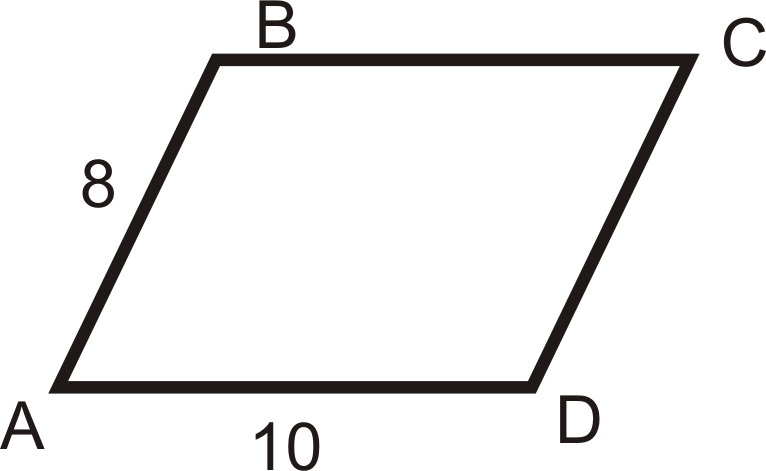
F-д_Ф2А8Е26А 77124Б145795E9D848 АД 2478Е85ЕФ 43293E46ADC0EF5FC+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{9}\)

\(k=2\), центр є\(D\)

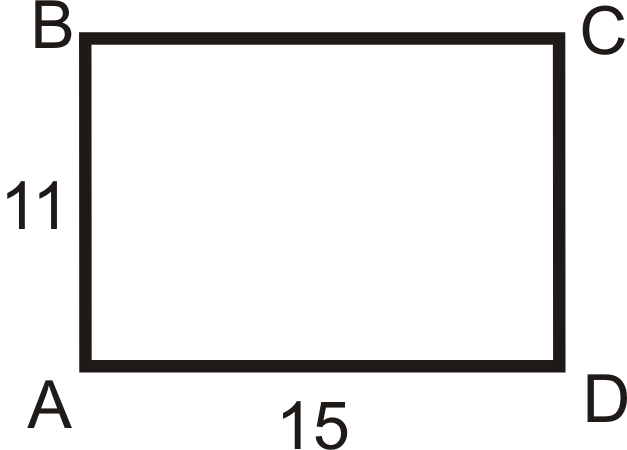
F-D_108B68250A18FCE762D94730Ф47952 CD2CF24462ДДДДФ62ДДФ 62232БДДФДДД+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{10}\)

\(k=\dfrac{3}{4}\), центр є\(A\)

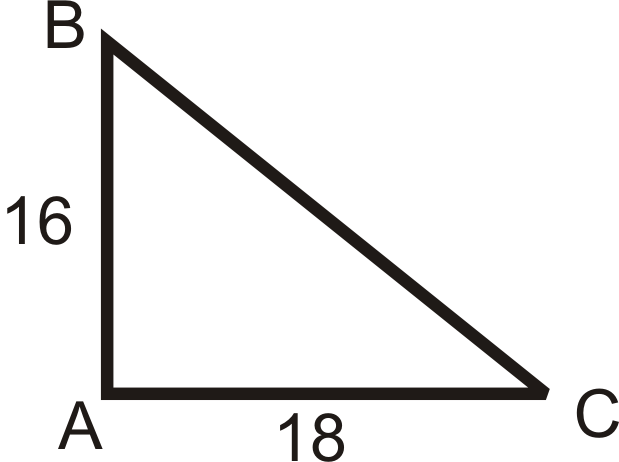
Ф-Д_1 АБ 555015Б90Е7КС4БД90БД9035Д20Е0912Е7С989Ф31Д3ДК91546+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{11}\)

\(k=\dfrac{2}{5}\), центр - А\)

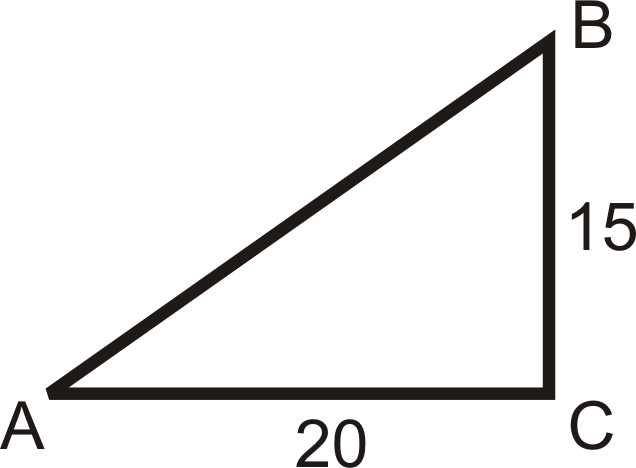
F-д_6500Б50Фе 4С5А43981651Б9С73 ЕДБ302835А029Ф489427Б36КБ28Б4+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{12}\)

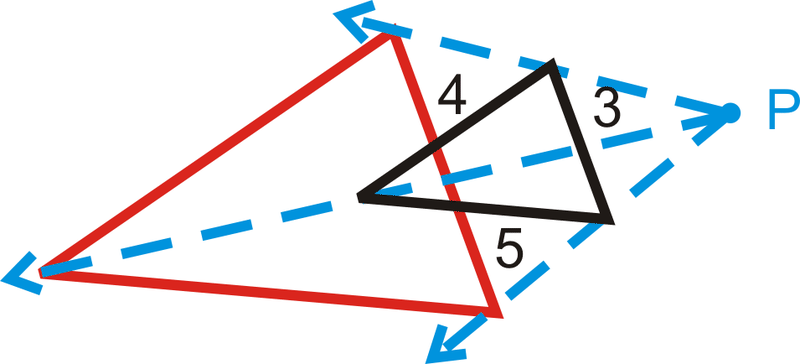
У чотирьох питаннях нижче вам розповідають про масштабний коефіцієнт. Визначте розміри розширення. На кожній схемі чорна фігура є оригіналом і\(P\) є центром розширення.

\(k=4\)

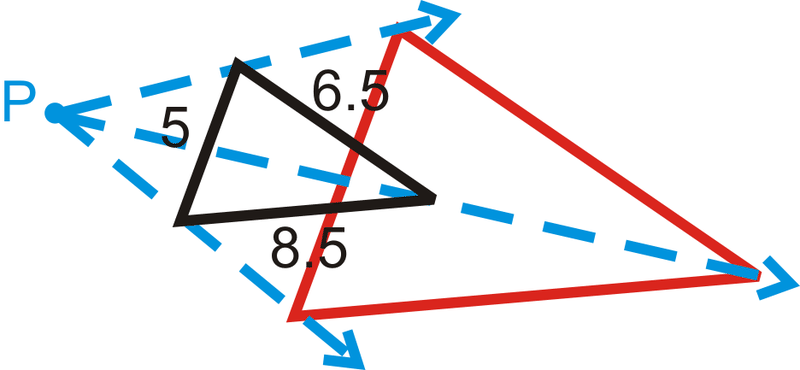
F-д_02235Ф9СБ7ЕД 8859781462896С6А07АЕ771АФ 9Е07Б71414Б98А6+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG — Малюнок\(\PageIndex{13}\)

\(k=\dfrac{1}{3}\)

F-D_1894Д916А 18925ДБ05С0С57Б81 ЕФ99Е240Е87С0КА40ЕБ929Б4Е73177+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{14}\)

\(k=2.5\)

F-D_B2B9 ФА8004034ЕАФ 0Б5А3485С960D2389725E08 АБКК 66357ББ0А5ФЕК+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{15}\)

\(k=\dfrac{1}{4}\)

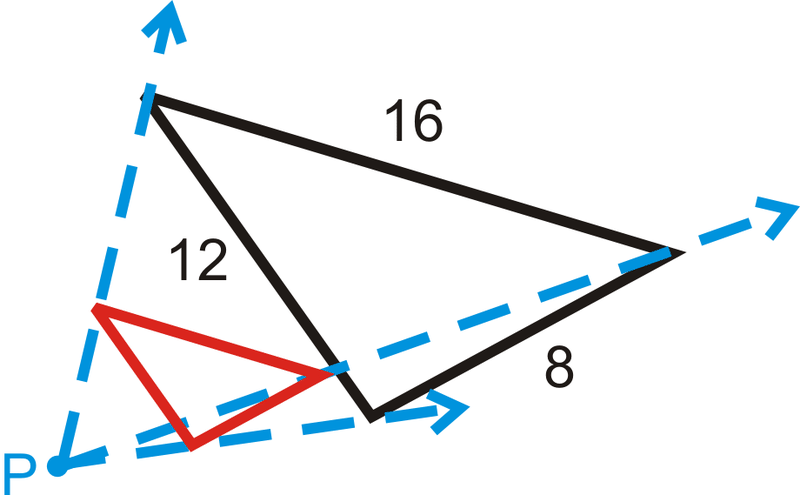
Ф-Д_1БД392 БДБ 823БДБ1Д8БД АФ 8БФ 4А52Д340Д710ДФ7БДК2БД БФ ББ5Б0648+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{16}\)

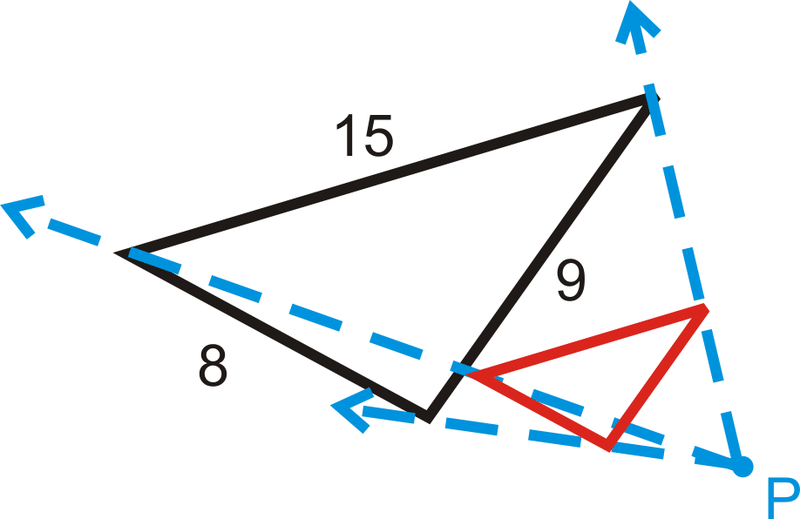
У трьох питаннях нижче знайдіть масштабний коефіцієнт, враховуючи відповідні сторони. На кожній схемі чорна фігура є оригіналом і\(P\) є центром розширення.

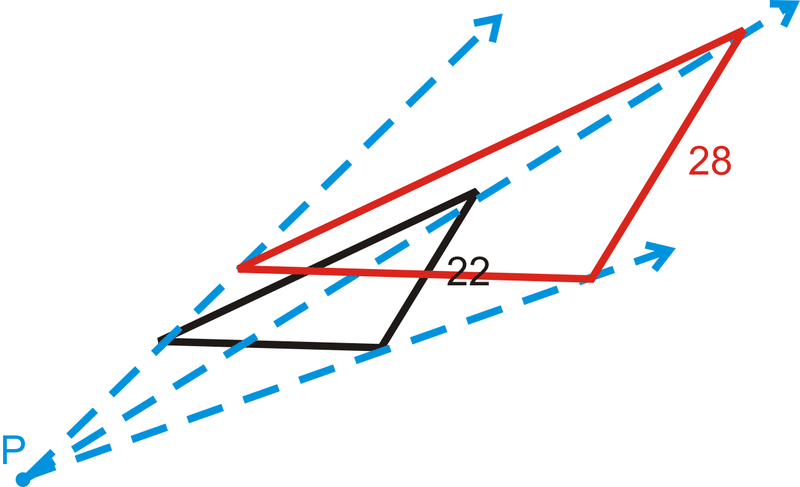
Малюнок\(\PageIndex{17}\)
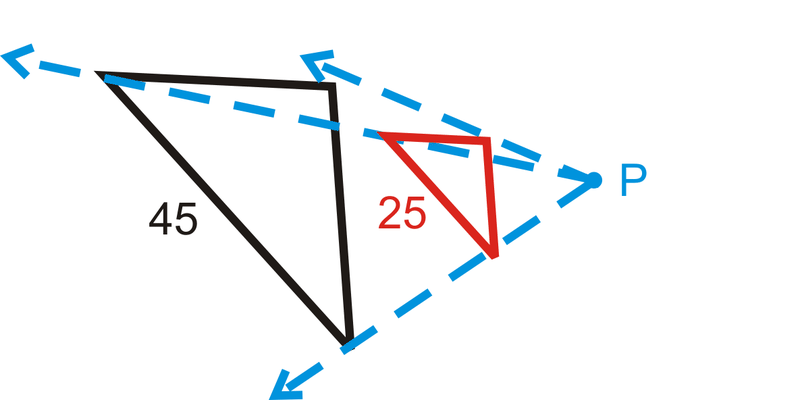
Малюнок\(\PageIndex{18}\)
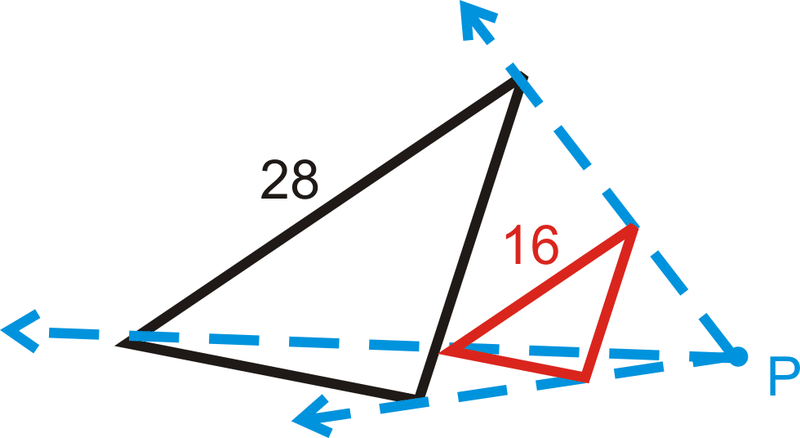
Малюнок\(\PageIndex{19}\)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 7.11.

Лексика

Термін	Визначення
Дилатація	Зменшити або збільшити цифру відповідно до масштабного коефіцієнта - це розширення.
Чотирикутник	Чотирикутник - замкнута фігура з чотирма сторонами і чотирма вершинами.
Співвідношення	Співвідношення - це порівняння двох величин, які можуть бути записані у вигляді дробу, з двокрапкою або зі словом «до».
Масштабний коефіцієнт	Масштабний коефіцієнт - це відношення масштабу до вихідного або фактичного виміру, написаного в найпростішій формі.
Трансформація	Перетворення певним чином переміщує фігуру на координатну площину.
Вершина	Вершина - це точка перетину ліній або променів, які утворюють кут.
Жорстке перетворення	Жорстке перетворення - це перетворення, яке зберігає відстань і кути, воно не змінює розмір або форму фігури.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи дилатації - Основні

Види діяльності: Дилатація Питання обговорення

Навчальні посібники: Види трансформацій Навчальний посібник

Практика: розширення форми

Реальний світ: Ефект CSI