7.13: Пропорції та бісектриси кута

Last updated

Oct 27, 2022
Save as PDF
- 7.12: Паралельні лінії, поперечні та пропорційність
- 7.14: Теореми, що стосуються подібності

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Кутові бісектриси ділять трикутники пропорційно.

Теорема про бісектрису кута

Коли кут всередині трикутника розділений, бісектриса ділить трикутник пропорційно. Ця ідея називається теоремою бісектриси кута.

Теорема про бісектрису кута: Якщо промінь розсікає кут трикутника, то він ділить протилежну сторону на відрізки, пропорційні довжинам двох інших сторін.

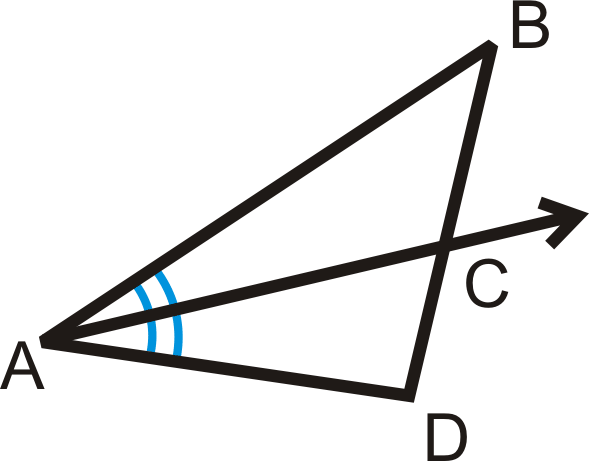
F-д_да 84Ф 356665739БА245А4 ЕБББ575Е160Д0958Б5Б5БФ84667475Б08ЕД765+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Якщо $\Delta BAC\cong \Delta CAD$ , то $\dfrac{BC}{CD}=\dfrac{AB}{AD}$ .

Що робити, якщо вам сказали, що промінь - це бісектриса кута трикутника? Як би ви використали цей факт, щоб знайти невідомі значення стосовно довжин сторін трикутника?

Приклад $\PageIndex{1}$

Заповніть відсутню змінну:

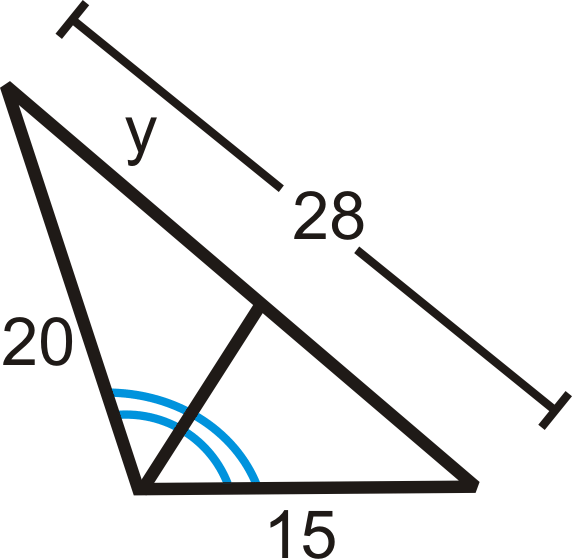
F-д_59445С1А5Е6ФБ90Б94191437 ДК 40Е381Ф1301Е8С0Ф36373БН62А003+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{2}$

Рішення

Налаштуйте пропорцію і вирішуйте.

$\begin{aligned} \dfrac{20}{y}&=\dfrac{15}{28−y} \\ 15y&=20(28−y) \\ 15y&=560−20y \\ 35y&=560 \\ y&=16\end{aligned}$

Приклад $\PageIndex{2}$

Заповніть відсутню змінну:

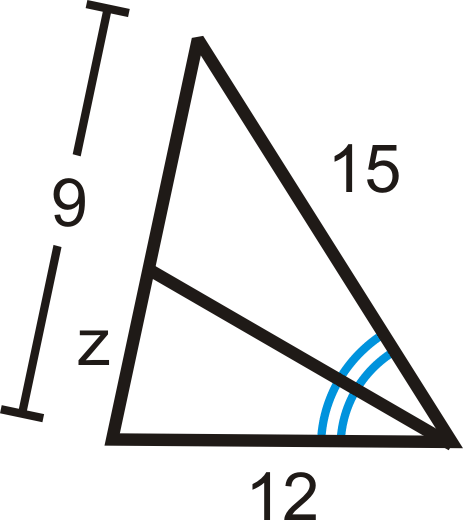
Ф-Д_557Б73КС3160ДБББ 5С81С50С78Бе710А47ДК53Е0960БДББН66А795БФ41+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Рішення

Налаштуйте пропорцію і вирішуйте.

$\begin{aligned}\dfrac{12}{z}&=\dfrac{15}{9−z} \\ 15z&=12(9−z) \\ 15z&=108-12z \\ 27z&=108 \\ z&=4\end{aligned}$

Приклад $\PageIndex{3}$

Знайти $x$ .

F-D_077 ДК 3197010 де17cdc9357863a8 фа7207bcb 1674d7b30163AE1A+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{4}$

Рішення

Промінь - це бісектриса кута, і він розщеплює протилежну сторону в тому ж співвідношенні, що і дві інші сторони. Пропорція становить:

$\begin{aligned} \dfrac{9}{x}&=\dfrac{21}{14} \\ 21x&=126 \\ x&=6\end{aligned}$

Приклад $\PageIndex{4}$

Знайдіть значення $x$ , яке зробить пропорцію істинною.

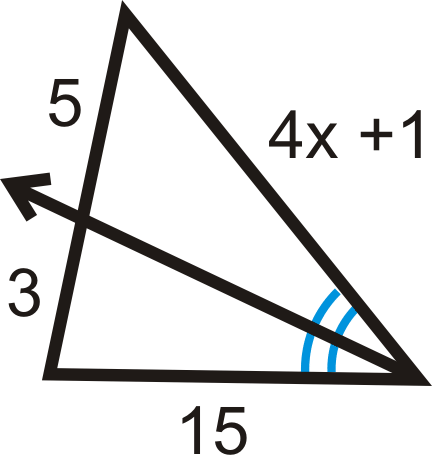
F-д_БББ063Д 9126 ЕД додати 133 фа633864c5E76c661b4186d6d6d6d65737784C78E+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{5}$

Рішення

Ви можете налаштувати цю пропорцію, як у попередньому прикладі.

$\begin{aligned} \dfrac{5}{3}&=\dfrac{4x+1}{15} \\ 75&=3(4x+1) \\ 75&=12x+3 \\ 72&=12x \\ 6&=x\end{aligned}$

Приклад $\PageIndex{5}$

Знайдіть відсутню змінну:

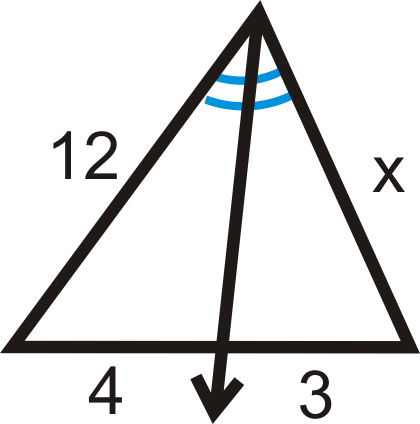
F-D_2d44b37c3732899C8D3Б2Ф2255Ф038АБ9Е6128795420DA3587C8B3F3FE+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{6}$

Рішення

Налаштуйте пропорцію і вирішуйте, як у попередніх прикладах.

$\begin{aligned}\dfrac{12}{4}&=\dfrac{x}{3} \\ 36&=4x \\ x&=9\end{aligned}$

Рецензія

Знайти значення відсутньої змінної (ів).

Малюнок $\PageIndex{7}$
Малюнок $\PageIndex{8}$

Вирішити для невідомої змінної.

Малюнок $\PageIndex{9}$
Малюнок $\PageIndex{10}$
Малюнок $\PageIndex{11}$
Малюнок $\PageIndex{12}$
Малюнок $\PageIndex{13}$
Малюнок $\PageIndex{14}$
Малюнок $\PageIndex{15}$
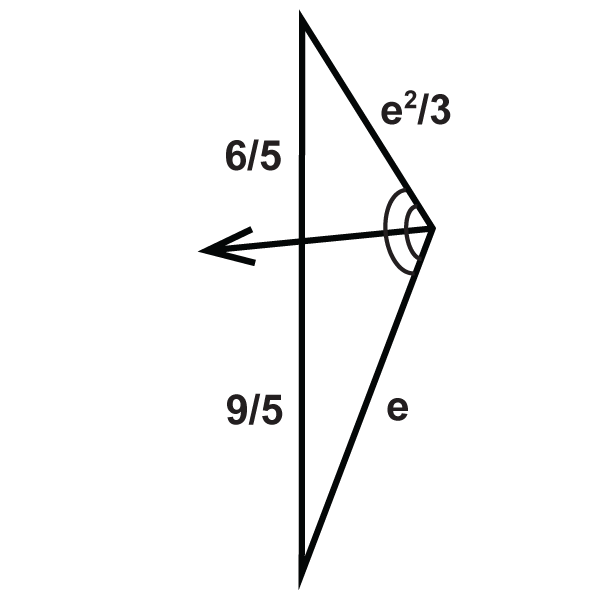
Малюнок $\PageIndex{16}$
Малюнок $\PageIndex{17}$
Малюнок $\PageIndex{18}$
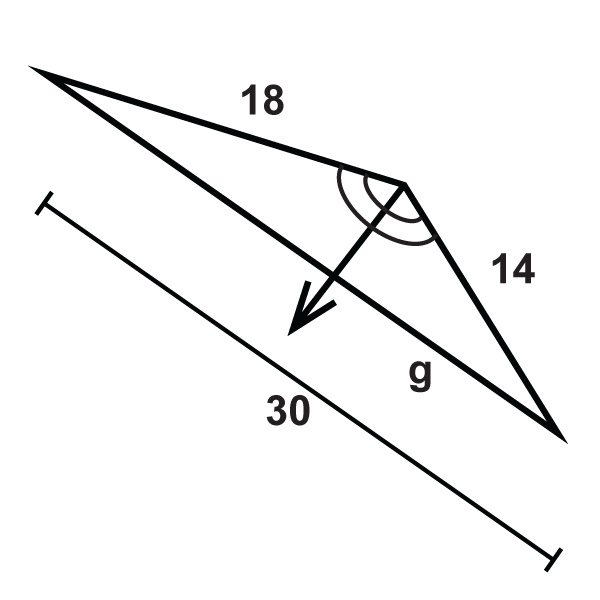
Малюнок $\PageIndex{19}$
Малюнок $\PageIndex{20}$
Малюнок $\PageIndex{21}$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 7.10.

Ресурси

Лексика

Термін	Визначення
бісектриса кута	Промінь, який ділить кут на два конгруентних кута.
Теорема про бісектрису кута	Теорема бісектриси кута стверджує, що якщо точка знаходиться на бісектрисі кута, то точка є рівновіддаленою від сторін кута.
Пропорція	Пропорція - це рівняння, яке показує два еквівалентних співвідношення.
Співвідношення	Співвідношення - це порівняння двох величин, які можуть бути записані у вигляді дробу, з двокрапкою або зі словом «до».

Додаткові ресурси

Інтерактивний елемент

Відео: Використання властивостей теореми про бісектрису трикутника для визначення невідомих значень

Діяльність: Пропорції з кутовими бісектрисами Питання обговорення

Навчальні посібники: Посібник з вивчення відносин пропорційності

Реальний світ: пропорційність трикутника