7.14: Теореми, що стосуються подібності

Last updated
Save as PDF

Page ID: 54696

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Доведіть та використовуйте пропорційність трикутника, бісектриса кута трикутника та теореми Піфагора.

Чи можете ви знайти будь-які подібні трикутники на малюнку нижче?

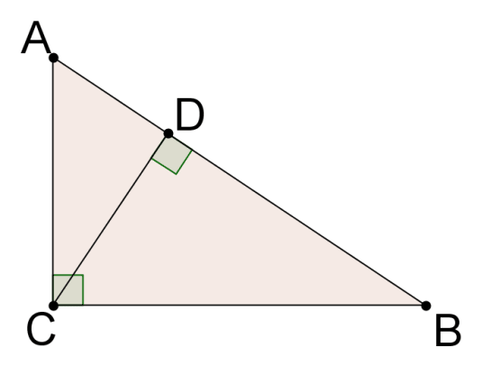
Теореми про подібні трикутники

Якщо два трикутника схожі, то відповідні їм кути конгруентні і відповідні їм сторони пропорційні. Існує багато теорем про трикутники, які можна довести, використовуючи подібні трикутники.

Теорема про пропорційність трикутника: Пряма, паралельна одній стороні трикутника, пропорційно розділяє дві інші сторони трикутника. Ця теорема та її зворотність будуть вивчені та доведені в #1 та #2, а також у вправах Огляд.
Теорема про бісектрису кута трикутника: Бісектриса кута одного кута трикутника ділить протилежну сторону трикутника на відрізки, пропорційні довжинам двох інших сторін трикутника. Ця теорема буде досліджена і доведена в #3.
Теорема Піфагора: Для прямокутного трикутника з катетами a і b та гіпотенузи c,\(a^2+b^2=c^2\). Ця теорема буде досліджена і доведена в задачах Приклади.

Давайте розглянемо деякі проблеми щодо доведення подібності трикутника.

1. Доведіть, що\(\Delta ADE\sim \Delta ABC\).

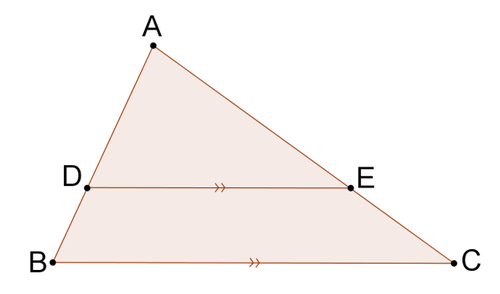
Два трикутника поділяють\(\angle A\). \(\overline{DE}\parallel \overline{BC}\)Тому що відповідні кути є конгруентними. Тому,\(\angle ADE\cong \angle ABC\). Два трикутника мають дві пари конгруентних кутів. Тому\(\Delta ADE\sim \Delta ABC\) по АА\ сім\).

2. Використовуйте свій результат від #1, щоб довести це\(\dfrac{AB}{AD}=\dfrac{AC}{AE}\). Потім використовуйте алгебру, щоб показати це\(\dfrac{DB}{AD}=\dfrac{EC}{AE}\).

\(\Delta ADE\sim \Delta ABC\)що означає, що відповідні сторони пропорційні. Тому,\(\dfrac{AB}{AD}=\dfrac{AC}{AE}\). Тепер ви можете використовувати алгебру, щоб показати, що друга пропорція повинна бути істинною. Пам'ятайте, що\(AB=AD+DB\) і\(AC=AE+EC\).

\(\begin{aligned}\dfrac{AB}{AD}&=\dfrac{AC}{AE} \\ \rightarrow \dfrac{AD+DB}{AD}&=AE+\dfrac{EC}{AE} \\ \rightarrow 1+\dfrac{DB}{AD}&=1+\dfrac{EC}{AE} \\ \rightarrow \dfrac{DB}{AD}&=\dfrac{EC}{AE}\end{aligned}\)

Тепер ви довели теорему пропорційності трикутника: лінія, паралельна одній стороні трикутника, пропорційно ділить дві інші сторони трикутника.

3. Розглянемо\(\Delta ABC\) з\(\overline{AE}\) кутом бісектриси\(\angle BAC\) і точка\(D\) побудована так, що\(\overline{DC}\parallel \overline{AE}\). Доведіть, що\(\dfrac{EB}{BA}=\dfrac{EC}{CA}\).

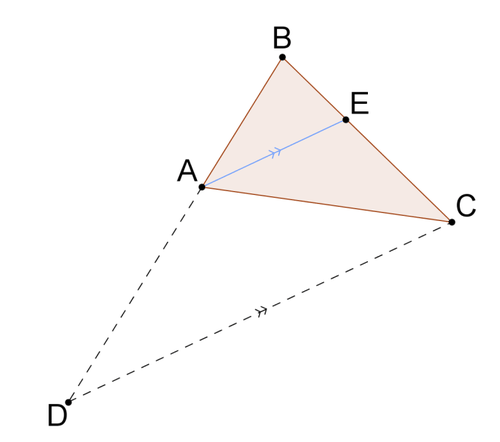
За теоремою пропорційності трикутника,\(\dfrac{EB}{EC}=\dfrac{BA}{AD}\). Помножте обидві сторони цієї пропорції на\(\dfrac{EC}{BA}\).

\(\begin{aligned}(\dfrac{EC}{BA})\cdot \dfrac{EB}{EC} \\ \rightarrow \dfrac{EB}{BA}=\dfrac{BA}{AD}\cdot (\dfrac{EC}{BA})=\dfrac{EC}{AD}\end{aligned}\)

Тепер все, що вам потрібно показати, це те, що для\(AD=CA\) того, щоб довести бажаний результат.

Тому що\(\overline{AE}\) це кут бісектриса\(\angle BAC\),\(\angle BAE\cong \angle EAC\).
Тому що\(\overline{DC}\parallel \overline{AE}\),\(\angle BAE\cong \angle BDC\) (відповідні кути).
Тому\(\overline{DC}\parallel \overline{AE}\),\(\angle EAC\cong \angle DCA\) (чергуйте внутрішні кути).
Таким чином,\(\angle BDC\cong \angle DCA\) за перехідним властивістю.

Тому\(\Delta ADC\) рівнобедрений, оскільки його базові кути конгруентні, і це повинно бути правдою\(\overline{AD}\cong \overline{CA}\). Це означає, що\(AD=CA\). Тому:

\(\dfrac{EB}{BA}=\dfrac{EC}{CA}\)

Це доводить теорему про бісектрису кута трикутника: бісектриса кута одного кута трикутника ділить протилежну сторону трикутника на відрізки, пропорційні довжинам двох інших сторін трикутника.

Приклад\(\PageIndex{1}\)

Раніше вас запитали, чи можна знайти будь-які подібні трикутники на малюнку нижче.

Рішення

На цій картині три трикутника:\(\Delta BAC\),\(\Delta BCD\),\(\Delta CAD\). Всі три трикутники є прямими трикутниками, тому вони мають один набір конгруентних кутів (прямий кут). \(\Delta BAC\)і\(\Delta BCD\) ділитися\(\angle B\), так\(\Delta BAC\sim \Delta BCD by \(AA\sim\). Аналогічно,\(\Delta BAC\) і\(\Delta CAD\) частка\(\angle C\), так\(\Delta BAC\sim \Delta CAD\) по\(AA\sim\). За перехідним властивістю всі три трикутника повинні бути схожі один на одного.

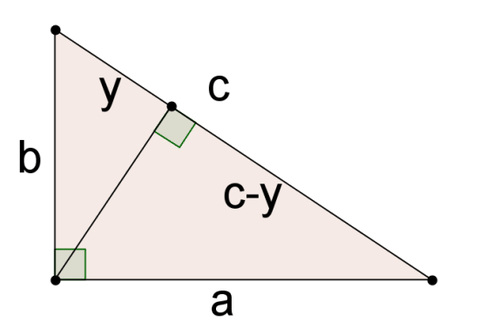
Великий трикутник вгорі має сторони\(a\)\(b\), і\(c\). Сторона\(c\) була розділена на дві частини:\(y\) і\(c−y\). У Повторному перегляді проблеми концепції ви показали, що три трикутники на цій картинці схожі.

Приклад\(\PageIndex{2}\)

Поясніть, чому\(\dfrac{a}{c}=\dfrac{c-y}{a}\).

Рішення

Коли трикутники схожі, відповідні сторони пропорційні. Ретельно зіставте відповідні сторони, і ви це бачите\(\dfrac{a}{c}=\dfrac{c-y}{a}\).

Приклад\(\PageIndex{3}\)

Поясніть, чому\(\dfrac{b}{c}=\dfrac{y}{b}\).

Рішення

Коли трикутники схожі, відповідні сторони пропорційні. Ретельно зіставте відповідні сторони, і ви це бачите\(\dfrac{b}{c}=\dfrac{y}{b}\).

Приклад\(\PageIndex{4}\)

Скористайтеся результатами #2 та #3, щоб показати це\(a^2+b^2=c^2\).

Рішення

Перехресне множення, щоб переписати кожне рівняння. Потім складіть два рівняння разом.

\(\begin{aligned} \dfrac{a}{c}&=\dfrac{c-y}{a}\rightarrow a^2=c^2−cy \\ \dfrac{b}{c}&=\dfrac{y}{b}\rightarrow b^2=cy \\ \rightarrow a^2+b^2&=c^2−cy+cy \\ \rightarrow a^2+b^2&=c^2 \end{aligned}\)

Ви щойно довели теорему Піфагора, використовуючи подібні трикутники.

Рецензія

Вирішити для\(x\) в кожній проблемі.

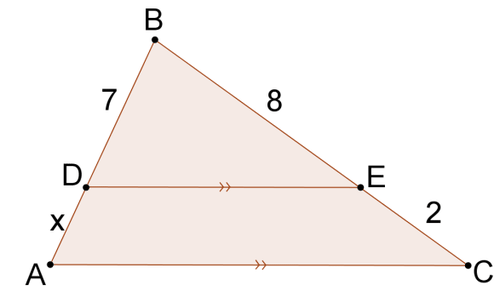
Малюнок\(\PageIndex{6}\)
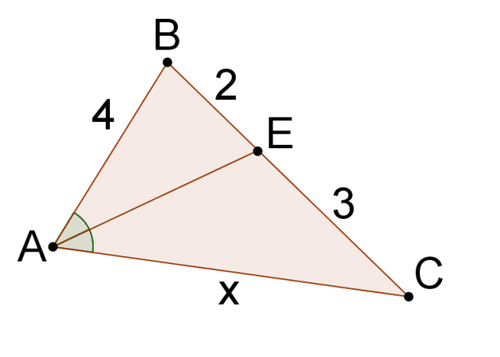
Малюнок\(\PageIndex{7}\)
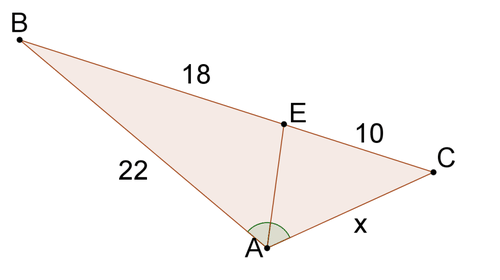
Малюнок\(\PageIndex{8}\)
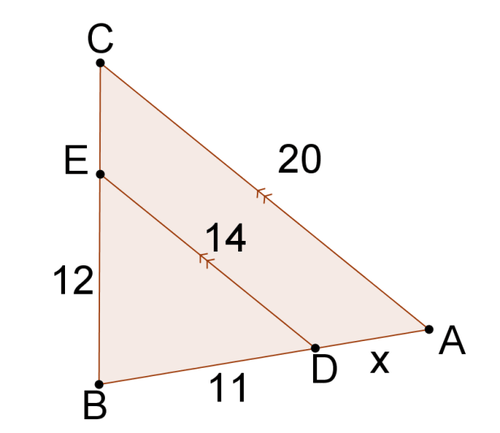
Малюнок\(\PageIndex{9}\)
Малюнок\(\PageIndex{10}\)
Малюнок\(\PageIndex{11}\)
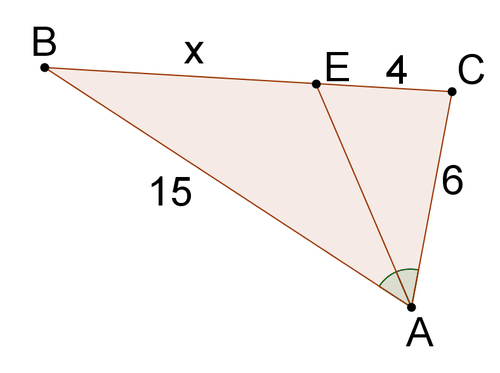
Малюнок\(\PageIndex{12}\)

Використовуйте малюнок нижче для #8 - #10.

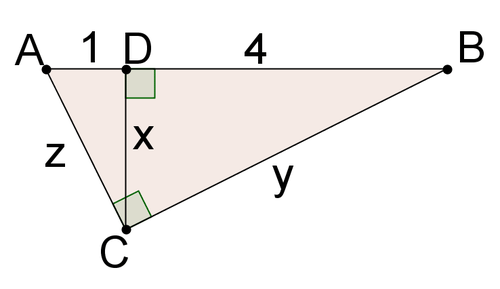
8. Вирішити для\(x\).

9. Вирішити для\(z\).

10. Вирішити для\(y\).

Використовуйте малюнок нижче для #11 - #13.

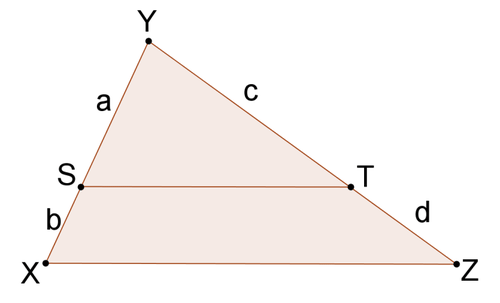
11. Припустимо, що\(\dfrac{b}{a}=\dfrac{d}{c}\). Використовуйте алгебру, щоб показати це\(\dfrac{b+a}{a}=\dfrac{d+c}{c}\).

12. Доведіть, що\(\Delta YST\sim \Delta YXZ\)

13. Доведіть, що\(\overline{ST}\parallel \overline{XZ}\)

14. Доведіть, що відрізок, який з'єднує середні точки двох сторін трикутника буде паралельно третій стороні трикутника.

15. Доведіть теорему Піфагора, використовуючи малюнок нижче.

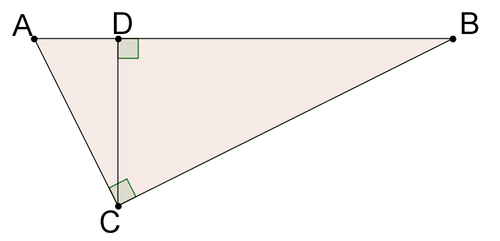
Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 6.6.

Лексика

Термін	Визначення
Теорема Піфагора	Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана\(a^2+b^2=c^2\), де\(a\) і\(b\) є катетами трикутника і\(c\) є гіпотенузою трикутника.
Теорема про пропорційність трикутника	Теорема про пропорційність трикутника стверджує, що якщо лінія паралельна одній стороні трикутника і вона перетинає дві інші сторони, то вона розділяє ці сторони пропорційно.
Теорема про бісектрису кута трикутника	Бісектриса кута одного кута трикутника ділить протилежну сторону трикутника на відрізки, пропорційні довжинам двох інших сторін трикутника.