7.12: Паралельні лінії, поперечні та пропорційність
- Page ID
- 54673
Як показала теорема про пропорційність трикутника, три або більше паралельних ліній, розрізаних двома поперечками, поділяють їх пропорційно.
Теорема про пропорційність трикутника
Теорема про пропорційність трикутника стверджує, що якщо лінія, паралельна одній стороні трикутника, перетинає дві інші сторони, то вона розділяє ці сторони пропорційно. Ми можемо розширити цю теорему до ситуації поза трикутниками, де ми маємо кілька паралельних ліній, розрізаних поперечками.
Теорема: Якщо дві або більше паралельних ліній розрізаються двома поперечками, то вони поділяють поперечки пропорційно.
 Малюнок\(\PageIndex{1}\)
Малюнок\(\PageIndex{1}\)Якщо\(l\parallel m\parallel n\), то\(\dfrac{a}{b}=\dfrac{c}{d}\) або\(\dfrac{a}{c}=\dfrac{b}{d}\).
Зауважте, що ця теорема працює для будь-якої кількості паралельних ліній з будь-якою кількістю поперек. Коли це відбувається, всі відповідні сегменти поперечок пропорційні.
Що робити, якщо ви дивилися на карту, на якій зображено чотири паралельні вулиці (A, B, C і D), розрізані двома проспектами, або поперечними, (1 і 2)? Як ви могли б визначити відстань, яку вам доведеться проїхати по проспекту 2, щоб дістатися до вулиці C від вулиці B, враховуючи відстань вниз по проспекту 1 від вулиці A до вулиці B, відстань вниз по проспекту 1 від вулиці B до C, і відстань вниз Авеню 2 від вулиці A до B?
Приклад\(\PageIndex{1}\)
Знайти\(a\),\(b\), і\(c\).

Рішення
Вирівняйте відрізки, які знаходяться один навпроти одного.
\ (\ begin {масив} {ccc}
\ гідророзриву {a} {9} =\ гідророзриву {2} {3} &\ гідророзриву {2} {3} =\ гідророзриву {4} {b} &\ frac {2} {3} =\ frac {3} {c}\
3 a=18 & 2 b=12 & 2 c=9\
a=6 & b=6 & b=6 6 & c = 4.5
\ кінець {масив}\)
Приклад\(\PageIndex{1}\)
Нижче наведено карту вулиць частини Вашингтона, округ Колумбія. R Street, Q Street та O Street паралельні, а 7-я вулиця перпендикулярна всім трьом. Всі виміри наведені на карті. Що таке х і у?

Рішення
Щоб знайти x і y, потрібно встановити пропорцію за допомогою паралельних ліній.
\(\dfrac{2640}{x}=\dfrac{1320}{2380}=\dfrac{1980}{y}\)
Від цього\(x=4760\text{ ft }\) і\(y=3570\text{ ft }\).

Приклад\(\PageIndex{1}\)
Знайти\(a\).

Рішення
Три лінії позначені паралельно, тому для вирішення задаємо пропорцію.
\(\begin{aligned}\dfrac{a}{20}&=\dfrac{9}{15} \\ 180&=15a \\ a&=12 \end{aligned}\)
Приклад\(\PageIndex{1}\)
Знайти\(b\).

Рішення
Для вирішення задайте пропорцію.
\(\begin{aligned} \dfrac{12}{9.6}&=\dfrac{b}{24} \\ 288&=9.6b \\ b&=30 \end{aligned}\)
Приклад\(\PageIndex{1}\)
Знайдіть значення x\), яке робить лінії паралельними.

Рішення
Для вирішення задайте пропорцію і вирішуйте для\(x\).
\(\begin{aligned}\dfrac{5}{8}&=\dfrac{3.75}{2x−4}\rightarrow 5(2x−4)&=8(3.75) \\ 10x−20&=30 \\ 10x&=50 \\ x&=5\end{aligned}\)
Рецензія
Значення кожної змінної знайдіть на картинках нижче.
-
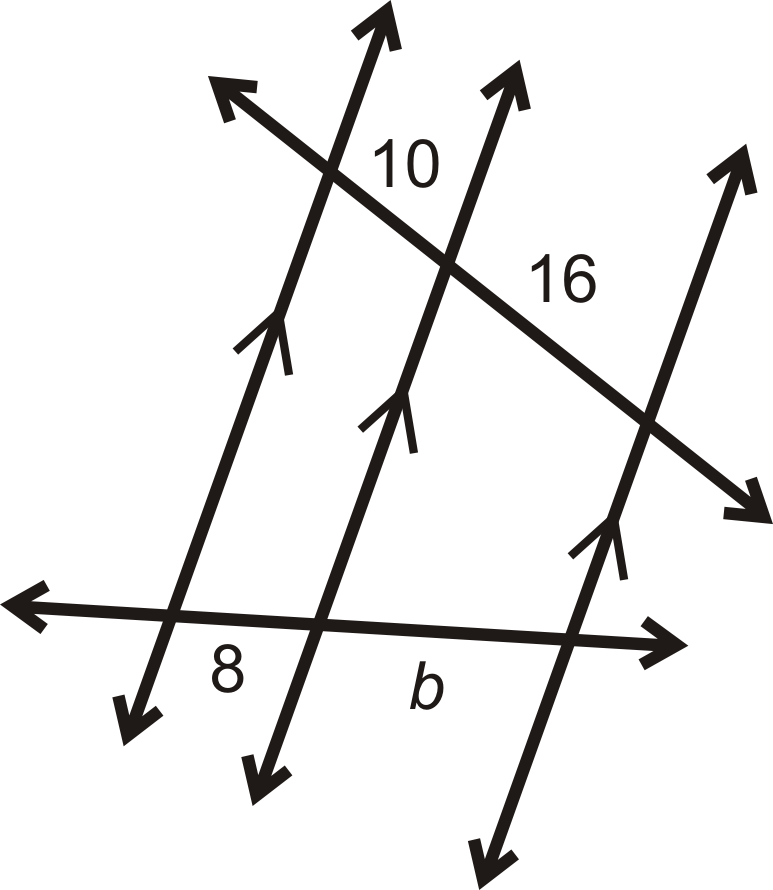
Малюнок\(\PageIndex{8}\) -

Малюнок\(\PageIndex{9}\) -

Малюнок\(\PageIndex{10}\) -

Малюнок\(\PageIndex{11}\) -

Малюнок\(\PageIndex{12}\)
Карта вулиць показує частину Нового Орлеана. Бургундська вул., Дофіна і Королівська Санкт-паралельні один одному. Якщо Spain St. перпендикулярна всім трьом, знайдіть зазначені відстані.
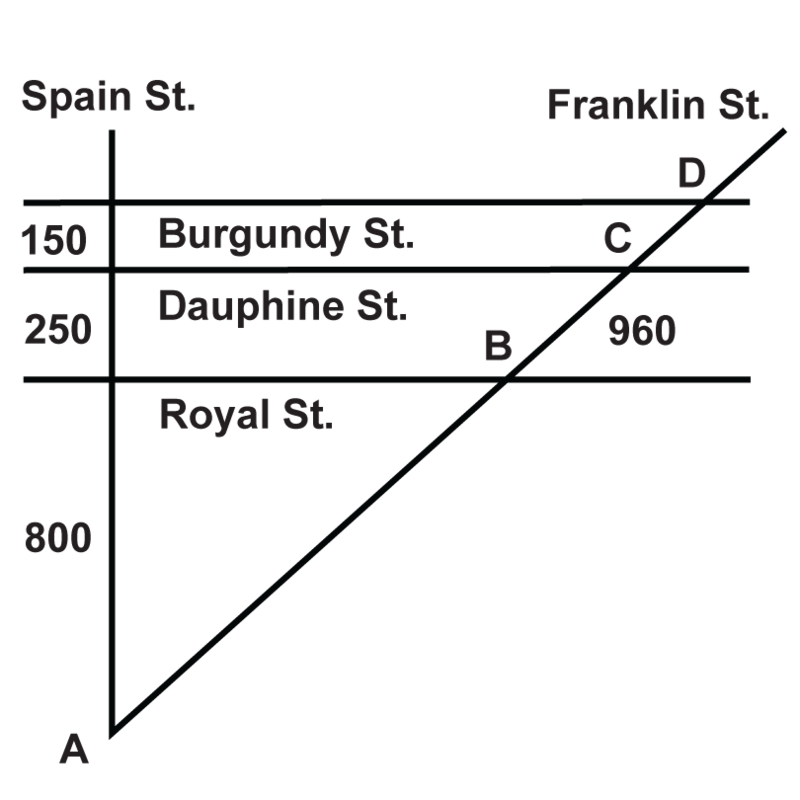
- Яка відстань між точками\(A\) і\(B\)?
- Яка відстань між точками\(C\) і\(D\)?
- Яка відстань між точками\(A\) і\(D\)?
Використовуючи схему, дайте відповідь на питання.
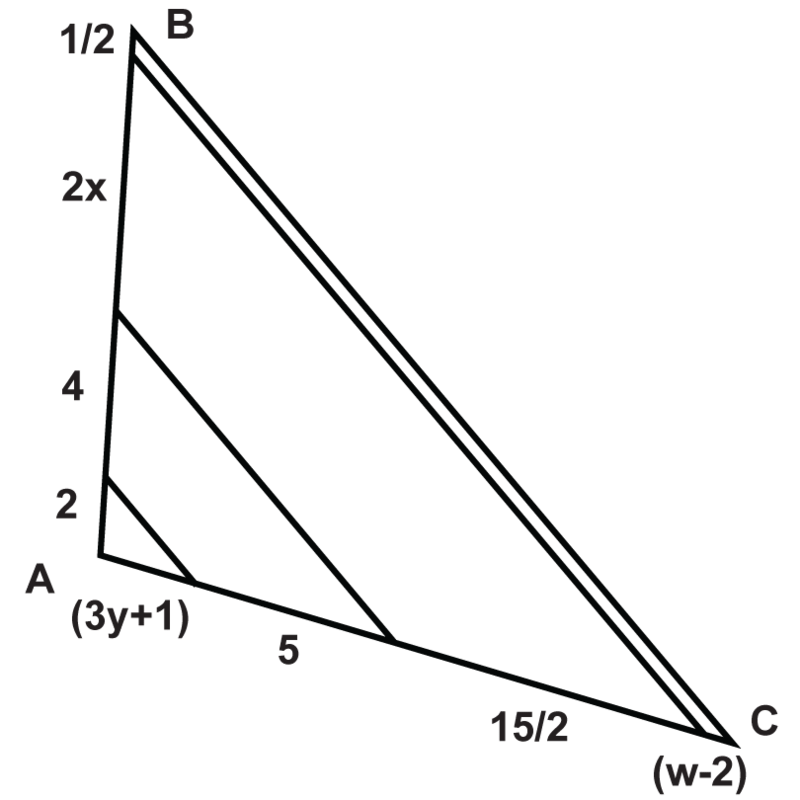
- Що таке цінність\(w\)?
- Що таке цінність\(x\)?
- Що таке цінність\(y\)?
- Яка довжина\(\overline{AB}\)?
- Яка довжина\(\overline{AC}\)?
Використовуючи схему, заповніть бланк.

- Якщо\(b\) третина\(d\), то\(a\) це ____________________.
- Якщо\(c\) два рази\(a\), то\(b\) це ____________________.
Огляд (Відповіді)
Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 7.9.
Лексика
| Термін | Визначення |
|---|---|
| Координатна площина | Координатна площина - це сітка, утворена горизонтальною цифровою лінією та вертикальною цифровою лінією, які перетинаються в точці (0, 0), яка називається початком. Координатна площина також називається декартовою площиною. |
| Перпендикуляр | Перпендикулярні лінії - це лінії, які перетинаються під кутом 90. Твір ухилів двох перпендикулярних ліній дорівнює -1. |
| Пропорція | Пропорція - це рівняння, яке показує два еквівалентних співвідношення. |
| Чотирикутник | Чотирикутник - замкнута фігура з чотирма сторонами і чотирма вершинами. |
| поперечний | Поперечна - це лінія, яка перетинає дві інші лінії. |
| Теорема про пропорційність трикутника | Теорема про пропорційність трикутника стверджує, що якщо лінія паралельна одній стороні трикутника і вона перетинає дві інші сторони, то вона розділяє ці сторони пропорційно. |
Додаткові ресурси
Інтерактивний елемент
Відео: Приклади паралельних ліній і поперек - Основні
Види діяльності: Паралельні лінії та поперечні обговорення Питання
Навчальні посібники: Посібник з вивчення пропорційності відносин
Практика: Паралельні лінії, поперечні та пропорційність
Реальний світ: паралельні лінії та поперечки