7.6: Застосування непрямих вимірювань

Last updated
Save as PDF

Page ID: 54642

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Використовуйте співвідношення та пропорції для вирішення відсутніх довжин у подібних цифрах у реальних ситуаціях.

Непряме вимірювання

Застосування подібних трикутників полягає у вимірюванні довжин побічно. Ви можете використовувати цей метод для вимірювання ширини річки або каньйону або висоти високого об'єкта. Ідея полягає в тому, що ви моделюєте ситуацію з подібними трикутниками, а потім використовуєте пропорції, щоб знайти відсутнє вимірювання побічно.

Що робити, якщо ви стояли поруч із будівлею і хотіли знати, наскільки висотою була будівля? Як ви могли використовувати власну висоту та довжину тіней, відкинутих вами та будівлею, щоб визначити висоту будівлі?

Для прикладів 1, 2 та 3 використовуйте наступну інформацію:

Для того щоб оцінити ширину річки, можна використовувати наступну методику. Скористайтеся схемою.

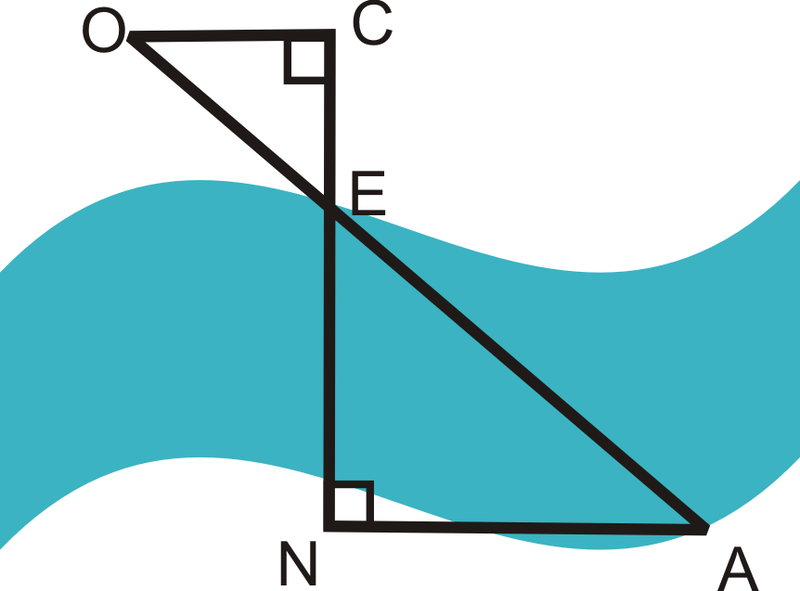
F-D_88 фек 1Б5131Б 11СБ 224Ф37БФ 1СА52ФФ Ф 735Е50СА8Б40175369+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Помістіть три маркери\(O\)\(C\),,, і\(E\) на верхньому березі річки. \(E\)знаходиться на краю річки і\(\overline{OC}\perp \overline{CE}\). Пройдіть через річку і поставте маркер,\(N\) щоб він був колінеарним з\(C\) і\(E\). Потім пройдіться по нижньому березі річки і розмістіть маркер A\), щоб\(\overline{CN}\perp \overline{NA}\). \(OC=50 feet\),\(CE=30\: feet\),\(NA=80\: feet\).

Приклад\(\PageIndex{1}\)

Є\(\Delta OCE\sim \Delta ANE\)? Звідки ти знаєш?

Рішення

Так. \(\angle C\cong \angle N\)тому що вони обидва прямі кути. \(\angle OEC\cong \angle AEN\)тому що вони є вертикальними кутами. Це означає\(\Delta OCE\sim \Delta ANE\) Постулат подібності AA.

Приклад\(\PageIndex{2}\)

Є\(\overline{OC}\parallel \overline{NA}\)? Звідки ти знаєш?

Рішення

Оскільки два трикутника схожі, ми повинні мати\(\angle EOC\cong \angle EAN\). Це чергові внутрішні кути. Коли альтернативні внутрішні кути конгруентні, то лінії паралельні, так\(\overline{OC}\parallel \overline{NA}\).

Приклад\(\PageIndex{3}\)

Яка ширина річки? Знайти\(EN\).

Рішення

Налаштуйте пропорцію і вирішуйте шляхом перехресного множення.

\(\dfrac{30\: ft}{EN}=\dfrac{50\: ft}{80\: ft}\)

\(50(EN)=2400\)

\(EN=48\)

Річка шириною 48 футів.

Приклад\(\PageIndex{4}\)

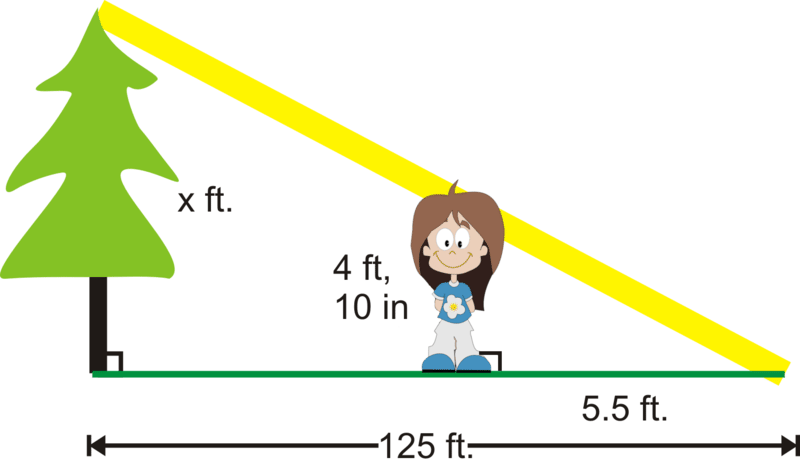
Дерево за межами будівлі Еллі відкидає 125-футову тінь. У той же час доби Еллі кидає тінь на 5,5 футів. Якщо Еллі 4 фути 10 дюймів заввишки, наскільки високе дерево?

F-д_ЕФ587С7Е7195С1CF4D4ЕФ6Ф2Б28А97570А5231Б273AB2AF7E8934C+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Рішення

Щоб вирішити, почніть з малювання малюнка. Ми бачимо, що дерево і Еллі паралельні, тому два трикутника схожі.

\(\dfrac{4\: ft,10\: in}{x}=\dfrac{5.5\: ft}{125\: ft}\)

Вимірювання потрібно проводити в однакових одиницях. Змініть все на дюйми, і тоді ми можемо перехрестити множення.

\(\dfrac{58\: in}{x}=\dfrac{66\: in}{1500\: in}\)

\(87000=66x\)

\(x\approx 1318.\overline{18} in or 109.85\: ft\)

Приклад\(\PageIndex{5}\)

Камерон має висоту 5 футів і кидає тінь 12 футів. У той же час доби сусідня будівля відкидає тінь на 78 футів. Наскільки висотою є будівля?

Рішення

Для вирішення задайте пропорцію, яка порівнює висоту з довжиною тіні для Камерона та будівлі. Потім вирішіть рівняння, щоб знайти висоту будівлі. Нехай х представляє висоту будівлі.

\ dfrac {5ft} {12\: ft} =\ dfrac {x} {78\: фут}\)

12х=390\)

x = 32,5\: фут\)

Висота будівлі становить 32,5 футів.

Рецензія

Методика з секції керованої практики використовувалася для вимірювання відстані через Гранд-Каньйон. Скористайтеся зображенням нижче і\(OC=72\: ft\)\(CE=65\: ft\), а\(NA=14,400\: ft\) для завдань 1 - 3.

1. Знайти\(EN\) (відстань через Гранд-Каньйон).

2. Знайти\(OE\).

3. Знайти\(EA\).

4. Марк має висоту 6 футів і відкидає тінь 15 футів. У той же час доби сусідня будівля відкидає 30-футову тінь. Наскільки висотою є будівля?

5. Карен і Джефф стоять поруч один з одним. Карен кидає тінь 10 футів, а Джефф кидає 8-футову тінь. Хто вище? Звідки ти знаєш?

6. Біллі має висоту 5 футів 9 дюймів, а Боббі - 6 футів у висоту. Тінь Боббі довжиною 13 футів. Скільки триває тінь Біллі?

7. Саллі та її маленький брат йдуть до школи. Саллі має висоту 4 фути і має тінь довжиною 3 фути. Тінь її маленького брата довжиною 2 фути. Наскільки високий її маленький брат?

8. Райан на вулиці грає в баскетбол. Він має висоту 5 футів і в цей час доби кидає тінь 12 футів. Баскетбольне кільце має висоту 10 футів. Скільки триває тінь баскетбольного кільця?

9. Джек стоїть поруч з дуже високим деревом і дивується, наскільки воно високе. Він знає, що він має висоту 6 футів і в цей момент його тінь довжиною 8 футів. Він вимірює тінь дерева і знаходить, що вона становить 90 футів. Наскільки високе дерево?

10. Томас, який має висоту 4 футів 9 дюймів, кидає тінь 6 футів. Сусідня будівля відливає тінь 42 футів. Наскільки висотою є будівля?

Ресурси

Лексика

Термін	Визначення
Постулат подібності AA	Якщо два кути в одному трикутнику збігаються з двома кутами в іншому трикутнику, то два трикутника схожі.
Пропорція	Пропорція - це рівняння, яке показує два еквівалентних співвідношення.

Додаткові ресурси

Інтерактивний елемент

Відео: Масштабні та непрямі вимірювання

Діяльність: Питання обговорення непрямих вимірювань

Навчальні посібники: Посібник з вивчення схожості полі

Практика: Застосування непрямих вимірювань

Реальний світ: Могутні вимірювання