Skip to main content
LibreTexts - Ukrayinska

7.11: Вписані подібні трикутники

  1. Last updated
  2. Save as PDF
  • Page ID
    54643

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Розподіл прямокутного трикутника на аналогічні трикутники за допомогою висоти.

    Теорема про вписані подібні трикутники

    Пам'ятайте, що якщо два об'єкти схожі, їх відповідні кути конгруентні, а сторони пропорційні по довжині. Висота прямокутного трикутника створює подібні трикутники.

    Вписані подібні трикутники Теорема: Якщо висота малюється від прямого кута будь-якого прямокутного трикутника, то два сформованих трикутника схожі на початковий трикутник, і всі три трикутники схожі один на одного.

    В\(\Delta ADB\),\(m\angle A=90^{\circ}\) і\(\overline{AC}\perp \overline{DB}\):

    Ф-д_8Ф94А81Ф6Д6Е18627А24 ББ14ЕД 0А48Е6А6А6АА6А6АА6АА506661ЕФА2Ф6А+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Отже,\(\Delta ADB\sim \Delta CDA\sim \Delta CAB\):

    F-д_59Б4Е955Д5ЕЕЕ8АБ 9073ФБ5Е137Б4 АБДА1 ЕЦ9Б702А2196Б47Е1018+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Це означає, що всі відповідні сторони пропорційні. Ви можете використовувати цей факт, щоб знайти відсутні довжини в правильних трикутниках.

    Що робити, якщо ви намалювали лінію від прямого кута прямокутного трикутника перпендикулярно стороні, яка протилежна цьому куту? Як ви могли визначити довжину цієї лінії?

    Приклад\(\PageIndex{1}\)

    Знайдіть значення\(x\).

    F-д_д12ф 225661a2c00f86576c2273e012eb8561ФДК1Б393434047C757+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Налаштуйте пропорцію.

    \(\begin{aligned} \dfrac{\text{ shorter leg in }\Delta SVT}{\text{ shorter leg in }\Delta RST}&=\dfrac{\text{ hypotenuse in }\Delta SVT}{ \text{ hypotenuse in }\Delta RST} \\ \dfrac{4}{x}&=\dfrac{x}{20} \\ x^2&=80 \\ x&=\sqrt{80}=4\sqrt{5} \end{aligned}\)

    Приклад\(\PageIndex{2}\)

    Тепер знайдіть значення\(y\) в\(\Delta RST\) вище.

    Рішення

    Використовуйте теорему Піфагора.

    \(\begin{aligned} y^2+(4\sqrt{5})^2&=20^2 \\y^2+80&=400 \\ y^2&=320 \\ y&=\sqrt{320}=8\sqrt{5}\end{aligned}\)

    Приклад\(\PageIndex{3}\)

    Знайдіть значення\(x\).

    F-д_2АЧБ 70c56937418b687c8657C7106c5c6267Б8168КБФ7Е8Б9E7991F2+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Відокремте трикутники, щоб знайти відповідні сторони.

    Ф-д_54б7769 АФБ 1783С429453Д3716496C24Ф8610049Е8БФ7С7568ДФББ+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Налаштуйте пропорцію.

    \(\begin{aligned} \dfrac{\text{ shorter leg in } \Delta EDG}{\text{ shorter leg in } \Delta DFG}&=\dfrac{\text{ hypotenuse in }\Delta EDG}{\text{ hypotenuse in }\Delta DFG} \\ \dfrac{6}{x}&=\dfrac{10}{8} \\ 48&=10x \\ 4.8&=x \end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Знайдіть значення\(x\).

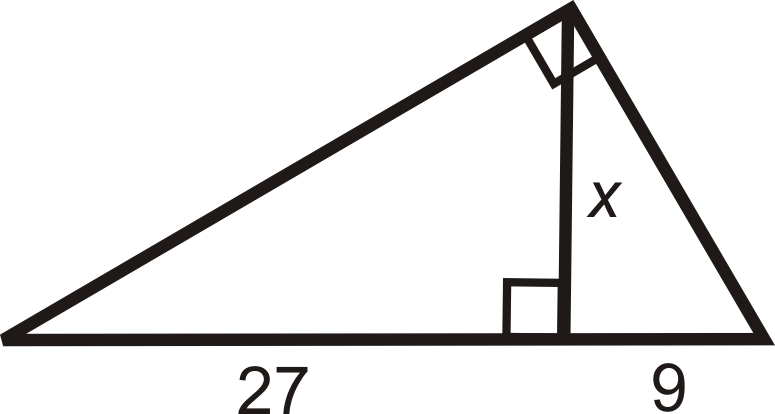
    Ф-Д_239Д4338244Ф87Д20932Ф26 CF26285ЕЕ377C3D51765C396884F36EF5+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Налаштуйте пропорцію.

    \(\begin{aligned}\dfrac{\text{ shorter leg of smallest }\Delta}{\text{ shorter leg of middle } \Delta}=\dfrac{ \text{ longer leg of smallest }\Delta }{\text{ longer leg of middle }\Delta} \\ \dfrac{9}{x}&=\dfrac{x}{27} \\ x^2&=243 \\ x&=\sqrt{243}=9\sqrt{3}\end{aligned}\)

    Приклад\(\PageIndex{5}\)

    Знайдіть значення\(x\) і\(y\).

    F-D_0cb387c3C521BAE9DC AC 7А60АА53 Дак 08Е59Д31Б735Б70АФ2Д1C5D9+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Відокремте трикутники. Напишіть пропорцію для\(x\).

    Рішення

    Ф-д_Б6Ф2Д6398038121А06С КАСБ 83Ф202БД42595А8Д774А6А949Ф515Б5Д+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)

    \(\begin{aligned} \dfrac{20}{x}&=\dfrac{x}{35} \\ x^2&=20\cdot 35 \\ x&=\sqrt{20\cdot 35} \\ x&=10\sqrt{7}\end{aligned}\)

    Налаштуйте пропорцію для y. Або тепер, коли ви знаєте значення x\), ви можете використовувати теорему Піфагора для розв'язання\(y\). Використовуйте метод, з яким ви відчуваєте себе найбільш комфортно.

    \ (\ почати {масив} {rlrl}
    \ frac {15} {y} & =\ розрив {y} {y} {35} & (10\ sqrt {7}) ^ {2} & =35^ {2}\
    y^ {2} & =15\ cdot 35 & 700+y^ {2} &=1225\\
    y & =\ sqrt {15\ cdot 35} & y&=\ sqrt {525} =5\ sqrt {21}\\ &
    y &=5\ sqrt {21}
    \ end {масив}\)

    Рецензія

    Заповніть заготовки.

    F-д_2А16Е1Е6Д98896E8F9D88A72551 ФК8С9С6Е6338Е19 ФЕБД 47251A3B98+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)
    1. \(\Delta BAD\sim \Delta ______ \sim \Delta ______\)
    2. \(\dfrac{BC}{?}=\dfrac{?}{CD}\)
    3. \(\dfrac{BC}{AB}=\dfrac{AB}{?}\)
    4. \(\dfrac{?}{AD}=\dfrac{AD}{BD}\)

    Напишіть заяву подібності для правильних трикутників на кожній діаграмі.

    1. F-д_КФ Ф 84 ББД БДФ ДБ6ЕД 9С403Д9Ф987А791ФЦ5Ф1782ДБ8373Е7Б4164+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
    2. F-D_82D536ФД 984657 ФБ ФБД 62Ф5С2БК 49357Е301279Д61А5F879E3DBE6+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)

    Використовуйте схему, щоб відповісти на питання 7-10.

    Ф-Д_ФДД 82ФД 5Д49Де 19Б0БФ де 9Ф65050С1ФДД2С51Е86Э9С62КБ5517C0CB6+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{12}\)
    1. Напишіть заяву подібності для трьох трикутників на схемі.
    2. Якщо\(JM=12\) і\(ML=9\), знайдіть\(KM\).
    3. Знайти\(JK\).
    4. Знайти\(KL\).

    Знайти довжину відсутньої змінної (s). Спрощення всіх радикалів.

    1. F-D_96ЕА0Б1 ЕЕБ 54E0D687D61 постійного струму 83299376553C50ЕД Д 5Д93А17А17АЦ7БФБ+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
    2. F-D_5CA2 AEFE 8Е9С10073191Б5Ф24Е12090ЕФ6847 ДБКД 339Ф3АЦФ396Ф57+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
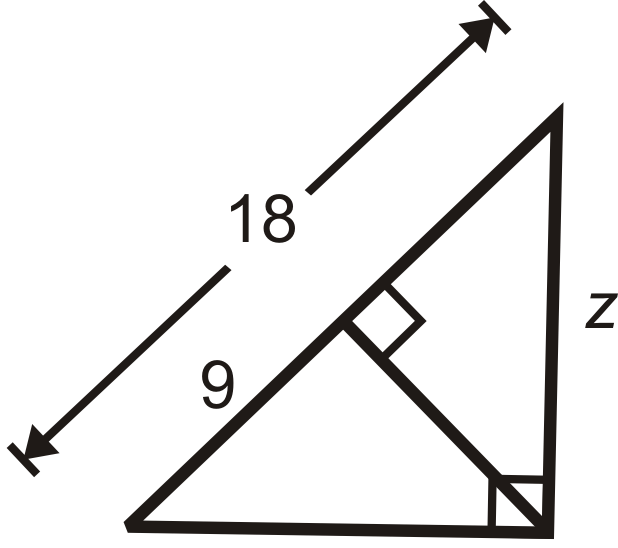
    3. F-д_ЕФ62Б478837977549C1F746020c87832CF71423d2Б94А9C8993F7+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
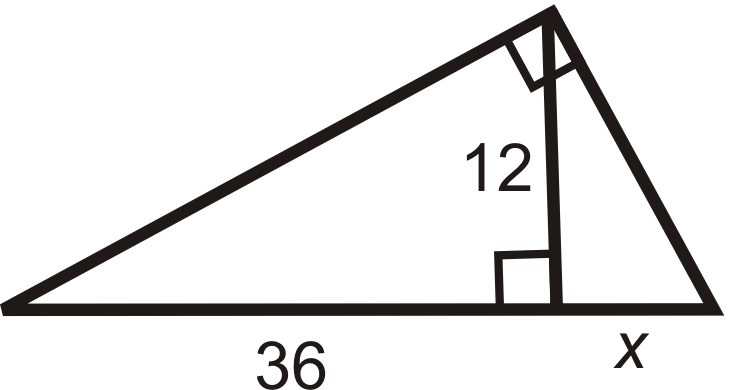
    4. Ф-Д_Д72979БД42Е7Д3681862 С66 А3Б460 Біл 01Д47320А99А698БС581А+зображення_крихіткий+зображення_крихітка_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
    5. F-д_Ф9С86ДФ 9Б8Д84БФ 894883ДФ8А12Б77С99Б7130Б205ЕБ39ДА3448D93E+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)
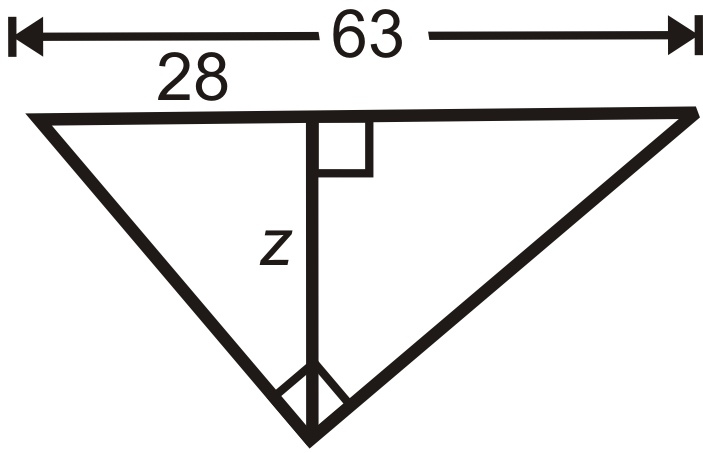
    6. F-D_165E624EA2A1671 CD8D31911Е47А782Е5ДФД9 Плата 47 AB30AC 90E5E4EC+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)
    7. F-D_EB67A311015D121D3Б0С3С804268Б636С68БЦ6Б8С63Д5С374БК+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)
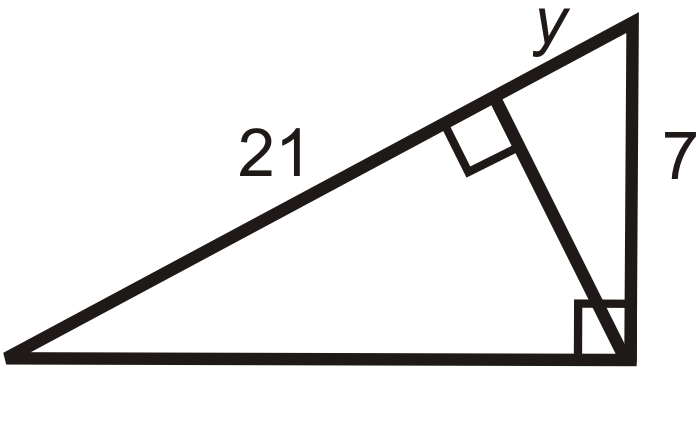
    8. F-д_ДБ9А3АА40А683422846Е859А3С0158БА 1Д465Б54ЕФ 015Б21Б33Б02+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{20}\)
    9. F-D_2769805332 СА338 ФЕ00448А 0ФК 2Д5де 0С84А35А1 АЦ36Б CDF8C6D9B9+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{21}\)
    10. F-D_62D431F72047E42B700F265Е АК 567Ф1Б8А2489103923ДБ6Ф68Ф3E3+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{22}\)
    11. F-д_8С4А 64125БД дек 9Ф8887736303881304D83A0Дбакс 0А217А06ФБФ26А+зображення_крихіткий+зображення_крихіткий.PNG
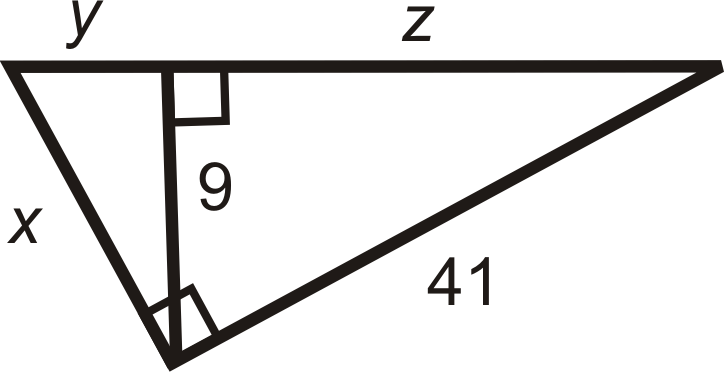
      Малюнок\(\PageIndex{23}\)
    12. F-д_Б7 Беб 9Е8Б653Д5Б387А1Ф3С5Д80А8А847Е26С1Д8393Ф283ЕЕ37Е44Д+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{24}\)
    13. Заповніть пробіли доказу для теореми про вписані подібні трикутники.
      F-д_2А16Е1Е6Д98896E8F9D88A72551 ФК8С9С6Е6338Е19 ФЕБД 47251A3B98+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{25}\)

    Дано:\(\Delta ABD\) з\(\overline{AC}\perp \overline{DB}\) і\(\angle DAB\) є прямим кутом.

    Доведіть:\(\Delta ABD\sim \Delta CBA\sim \Delta CAD\)

    Заява Причина
    1. 1. Враховується
    2. \(\angle DCA\)і\(\angle ACB\) є прямими кутами 2.
    3. \(\angle DAB\cong \angle DCA\cong \angle ACB\) 3.
    4. 4. Рефлексивний PoC
    5. 5. Постулат подібності AA
    6. \(B\cong \angle B\) 6.
    7. \(\Delta CBA\cong \Delta ABD\) 7.
    8. \(\Delta CAD\cong \Delta CBA\) 8.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.4.

    Лексика

    Термін Визначення
    Теорема про вписані подібні трикутники Теорема про вписані подібні трикутники стверджує, що якщо висота малюється від прямого кута будь-якого прямокутного трикутника, то два сформованих трикутника схожі на початковий трикутник, і всі три трикутники схожі один на одного.
    Перпендикуляр Перпендикулярні лінії - це лінії, які перетинаються під кутом 90. Твір ухилів двох перпендикулярних ліній дорівнює -1.
    Пропорція Пропорція - це рівняння, яке показує два еквівалентних співвідношення.
    Теорема Піфагора Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана\(a^2+b^2=c^2\), де a і b - катети трикутника, а c - гіпотенуза трикутника.

    Додаткові ресурси

    Відео: Вписані аналогічні принципи трикутників - Основні

    Діяльність: Вписані подібні трикутники Обговорення Питання

    Навчальні посібники: Посібник з вивчення подібності прямокут

    Практика: Вписані подібні трикутники

    Реальний світ: Вписані схожі трикутники