Skip to main content
LibreTexts - Ukrayinska

7.10: Пропорційні трикутники

  1. Last updated
  2. Save as PDF
  • Page ID
    54674

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Сторони розділені лінією, паралельною третій стороні трикутника.

    Теорема про пропорційність трикутника

    Подумайте про середній сегмент трикутника. Середній сегмент паралельний одній стороні трикутника і ділить дві інші сторони на конгруентні половини. Середній сегмент розділяє ці дві сторони пропорційно. Але як щодо іншої лінії, яка паралельна, але не ділить дві інші сторони на конгруентні половини? Насправді така лінія все одно розділить сторони пропорційно. Це називається теоремою пропорційності трикутника.

    Теорема про пропорційність трикутника: Якщо лінія, паралельна одній стороні трикутника, перетинає дві інші сторони, то вона розділяє ці сторони пропорційно.

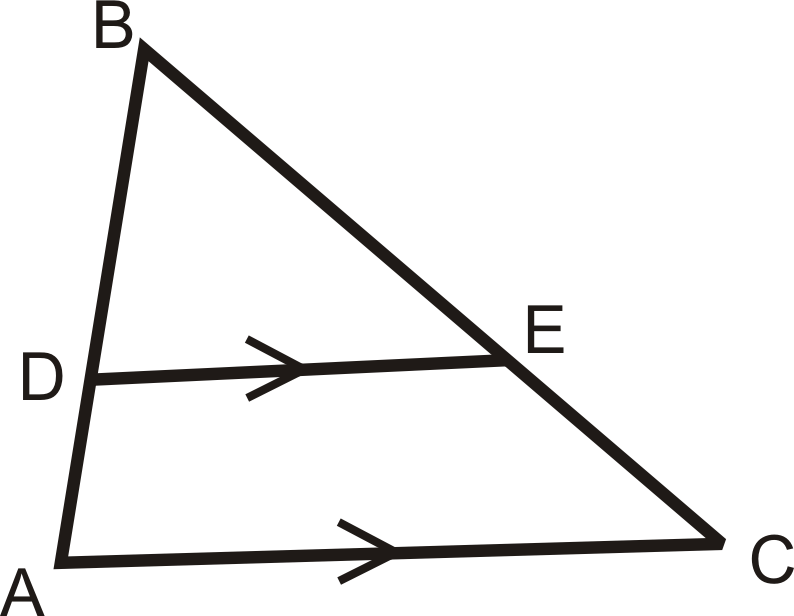
    F-д_527е8д 7229А4С872ДД81584е54Б7Б7Б 7Б74 А2Д35С5Е1705993Ф33Б+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Якщо\(\overline{DE}\parallel \overline{AC}\), то\(\dfrac{BD}{DA}=\dfrac{BE}{EC}\). (\(\dfrac{DA}{BD}=\dfrac{EC}{BE}\)Це також справжня пропорція. )

    Вірно і зворотне значення цієї теореми.

    Теорема пропорційності трикутника Converse: Якщо лінія розділяє дві сторони трикутника пропорційно, то вона паралельна третій стороні.

    Якщо\(\dfrac{BD}{DA}=\dfrac{BE}{EC}\), то\(\overline{DE}\parallel \overline{AC}\).

    Що робити, якщо вам дали трикутник з відрізком лінії, проведеним через нього з одного боку на інший? Як ви можете використовувати інформацію про довжину сторін трикутника, щоб визначити, чи цей відрізок лінії паралельний третій стороні?

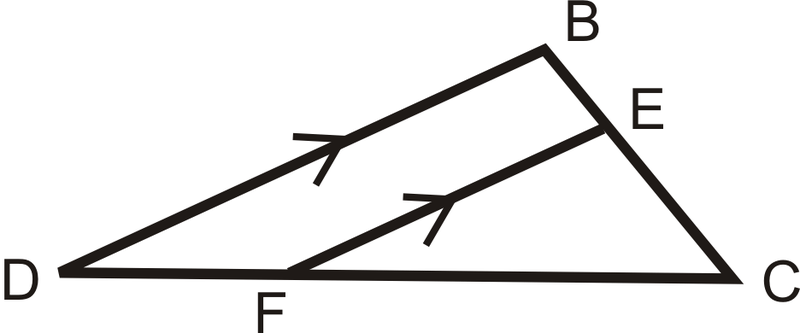
    Використовуйте діаграму для відповідей Приклади 1 і 2. \(\overline{DB}\parallel \overline{FE}\).

    F-D_CF96C3C6F1D64E644976 AB7CCC8C70795 ФА98С347 ABFF59D021DE9B8+зображення_крихіткий+зображення_крихітковий_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Приклад\(\PageIndex{1}\)

    Назвіть подібні трикутники. Напишіть заяву подібності.

    Рішення

    \(\Delta DBC\sim \Delta FEC\)

    Приклад\(\PageIndex{2}\)

    \(\dfrac{FC+?}{FC}=\dfrac{?}{FE}\)

    Рішення

    \(DF\);\(DB\)

    Приклад\(\PageIndex{3}\)

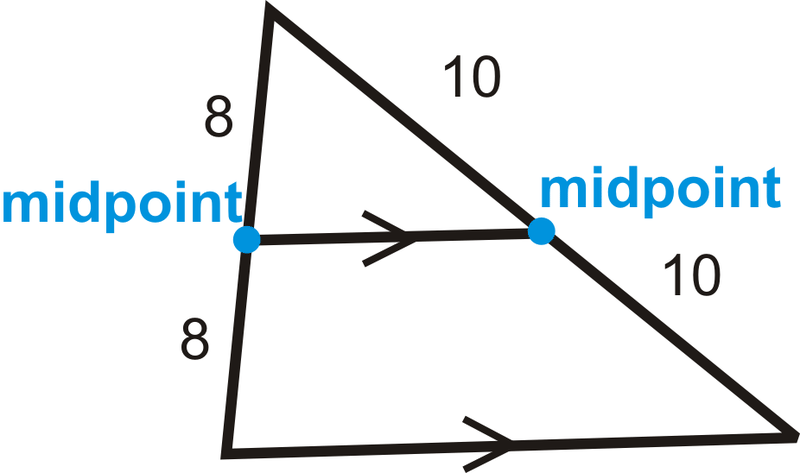
    Нижче малюється трикутник з його середнім відрізком. Яке співвідношення, на яке серединний сегмент ділить сторони?

    F-д_6а 68693Д149БД1ДФ7051Ф07КС3Б27885Д785Д3Ф07Ф2Е7Е0Е1Ф6Б4Е1+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Середній сегмент розщеплює сторони рівномірно. Співвідношення буде 8:8 або 10:10, які обидва зменшуються до 1:1.

    Приклад\(\PageIndex{4}\)

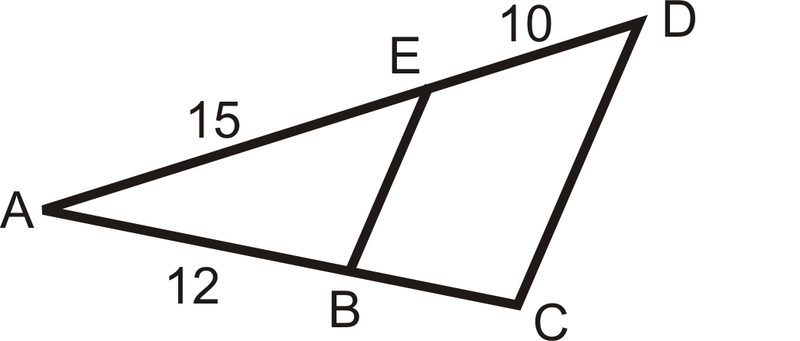
    На схемі нижче,\(\overline{EB}\parallel \overline{CD}\). Знайти\(BC\).

    Ф-д_13Е4КББФ 6КФ4Д9С24ФД0 ЕС217к40649БА2С89С6Д1207427128Д93С0+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Для вирішення задайте пропорцію.

    \(\begin{aligned} \dfrac{10}{15}=\dfrac{BC}{12} \rightarrow 15(BC)&=120 \\ BC&=8 \end{aligned}\)

    Приклад\(\PageIndex{5}\)

    Є\(\overline{DE}\parallel \overline{CB}\)?

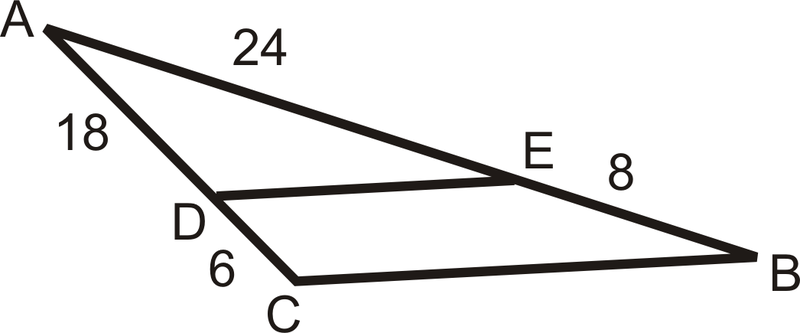
    F-D_9A9 CAE 937C4A24316973E56BA77A0CF95E3A5AEDC18BBC7C3FDD076+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Якщо співвідношення рівні, то лінії паралельні.

    \(\dfrac{6}{18}=\dfrac{8}{24}=\dfrac{1}{3}\)

    Тому що співвідношення рівні,\(\overline{DE}\parallel \overline{CB}\).

    Рецензія

    Використовуйте діаграму, щоб відповісти на питання 1-7. \(\overline{AB}\parallel \overline{DE}\).

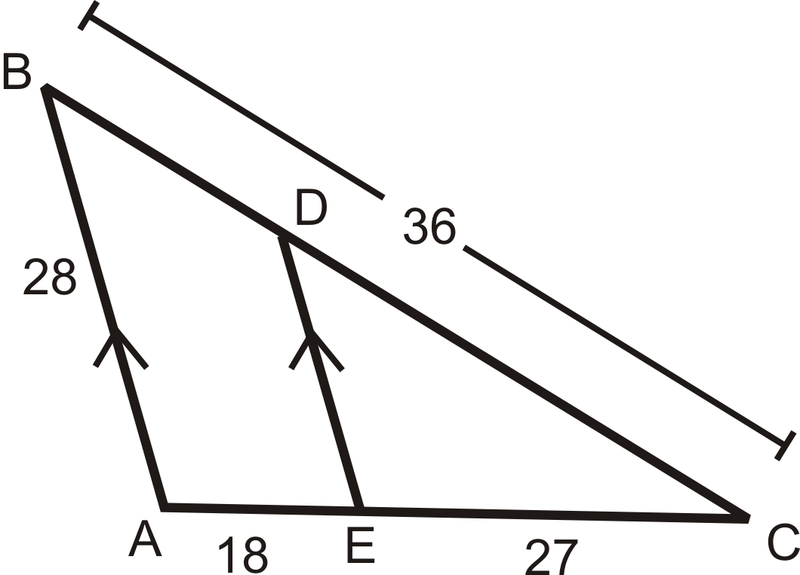
    F-д_42 бе 0дд 70828A51e6167EF мертвий 147579ФБ8347А98Ф23552861 DC93F93F9+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)
    1. Знайти\(BD\).
    2. Знайти\(DC\).
    3. Знайти\(DE\).
    4. Знайти\(AC\).
    5. Що таке\(BD:DC\)?
    6. Що таке\(DC:BC\)?
    7. Чому\(BD:DC\neq DC:BC\)?

    Використовуйте задані довжини, щоб визначити, якщо\(\overline{AB}\parallel \overline{DE}\).

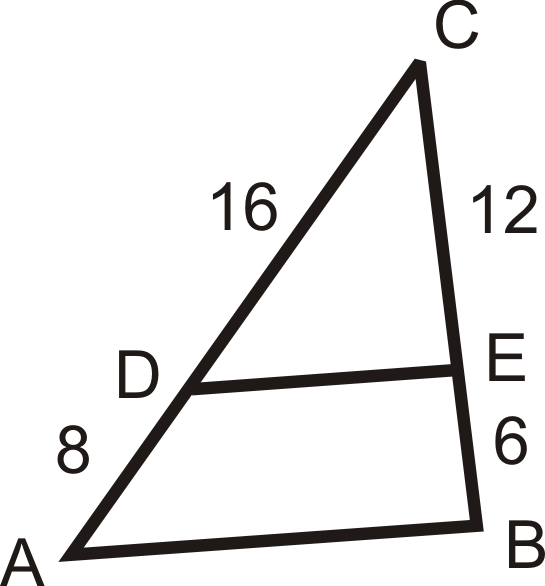
    1. F-д_59Д0ДФФ 411А8Д2Ф59А82Б98742А 7БД680Д3Б562482257247ДФБ6Е8ДФ+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
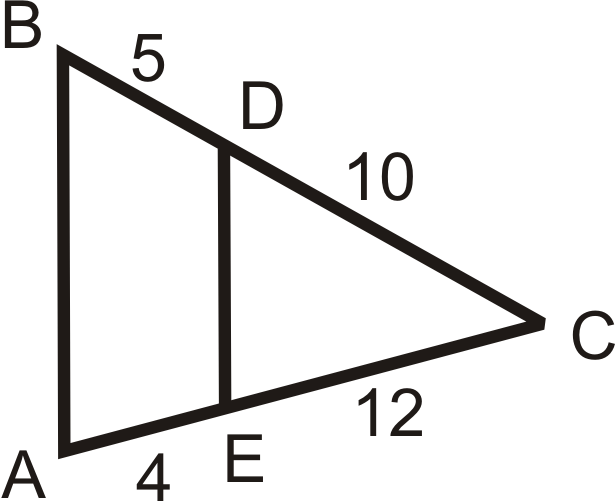
    2. F-D_BB48652D23190094982B04039 Додати 91E7E5436B8AAFC98FD0B BE39D+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
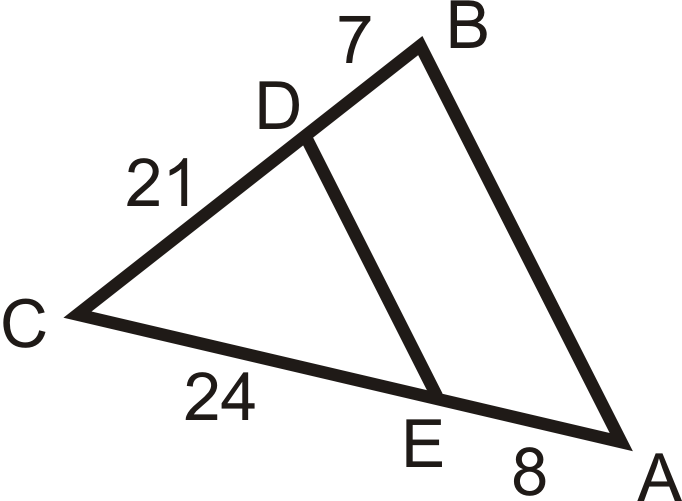
    3. F-D_0101d35Е9А5А3Е01А4ЕД 7Б2Д258485413 DC CA1FE2B94262D7C9+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
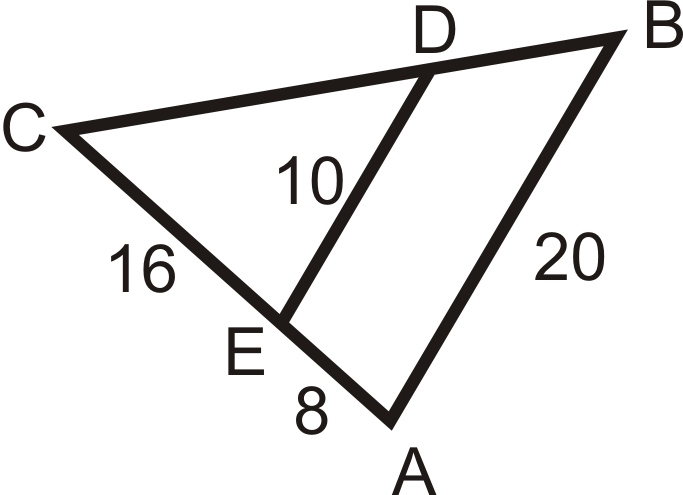
    4. F-д_Ф6 СБ319 ФД 000335345 СА3БФ2А АБ0Б2Б057 ФЕА 534E9344D1529E663C+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
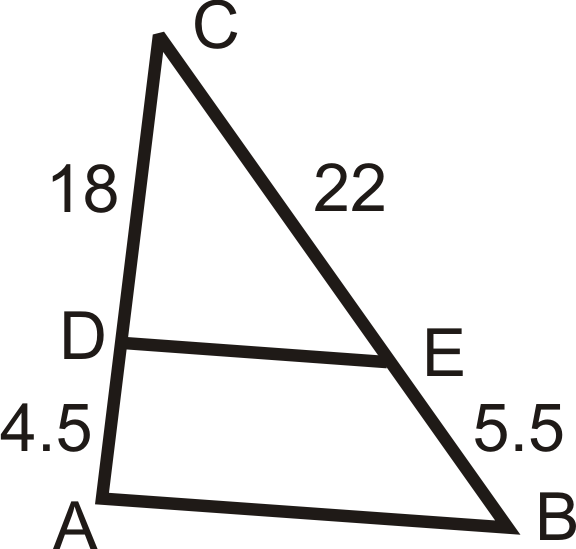
    5. F-д_CCC 46709А6Ф79де6610Е1420 ЕЕФ68924Е89Ф88Ф52Е8ЕД 49С2884Д0Б2+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
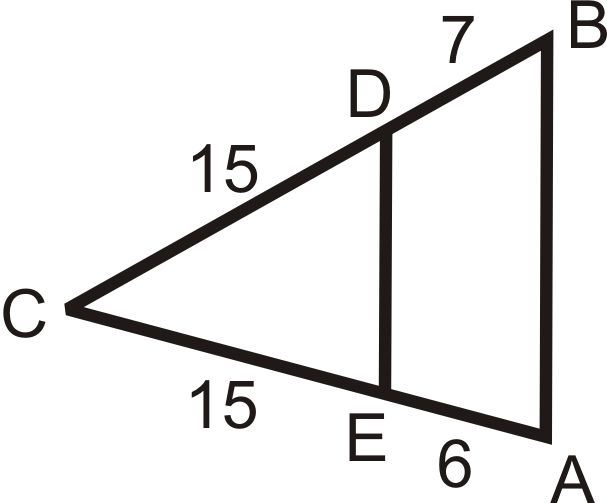
    6. F-D_5C775B6CA6CA60823E2042D63Б35Ф1Д2АЦ306ФЦ6517C0C ЕБ0ЕФ 493+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 7.8.

    Ресурси

    Лексика

    Термін Визначення
    Конгруентний Конгруентні фігури ідентичні за розміром, формою і мірою.
    середній сегмент Середній сегмент з'єднує середні точки двох сторін трикутника або непаралельних сторін трапеції.
    Паралельний Дві або більше ліній паралельні, коли вони лежать в одній площині і ніколи не перетинаються. Ці лінії завжди будуть мати однаковий нахил.
    Пропорція Пропорція - це рівняння, яке показує два еквівалентних співвідношення.
    Теорема про пропорційність трикутника Теорема про пропорційність трикутника стверджує, що якщо лінія паралельна одній стороні трикутника і вона перетинає дві інші сторони, то вона розділяє ці сторони пропорційно.
    Теорема пропорційності трикутника Зворотна теорема пропорційності трикутника стверджує, що якщо пряма розділяє дві сторони трикутника пропорційно, то вона паралельна третій стороні.

    Додаткові ресурси

    Відео: Використання властивостей теореми пропорційності трикутника для розв'язання невідомих значень

    Діяльність: Питання обговорення пропорційності трикутника

    Навчальні посібники: Посібник з вивчення пропорційності відносин

    Практика: Пропорційні трикутники

    Реальний світ: пропорційність трикутника