Skip to main content
LibreTexts - Ukrayinska

7.9: Схожість SAS

  1. Last updated
  2. Save as PDF
  • Page ID
    54686

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Трикутники схожі, якщо дві пари сторін пропорційні, а включені кути є конгруентними.

    Теорема подібності SAS

    За визначенням два трикутника схожі, якщо всі відповідні їм кути конгруентні, а відповідні їм сторони пропорційні. Не обов'язково перевіряти всі кути і сторони, щоб визначити, чи схожі два трикутника. Насправді, якщо ви знаєте лише, що дві пари сторін пропорційні, а їхні включені кути є конгруентними, цього достатньо інформації, щоб знати, що трикутники схожі. Це називається теоремою подібності SAS.

    Теорема подібності SAS: Якщо дві сторони в одному трикутнику пропорційні двом сторонам іншого трикутника, а включений кут в обох є конгруентними, то два трикутники схожі.

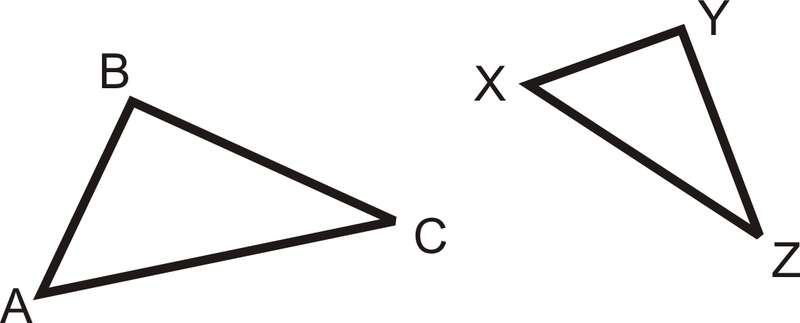
    Ф-д_Б6480Е8 де 58638D9 АД АД ББ2Д2С9Е2Ф9533 ББК 87А3Ф86CE2078519+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Якщо\(\dfrac{AB}{XY}=\dfrac{AC}{XZ}\) і\(\angle A\cong \angle X\), то\(\Delta ABC\sim \Delta XYZ\).

    Що робити, якщо вам дали пару трикутників, довжини двох їх сторін, і міра кута між цими двома сторонами? Як ви могли б використовувати цю інформацію, щоб визначити, чи два трикутники схожі?

    Приклад\(\PageIndex{1}\)

    Визначте, чи схожі наступні трикутники. Якщо так, напишіть теорему подібності і твердження.

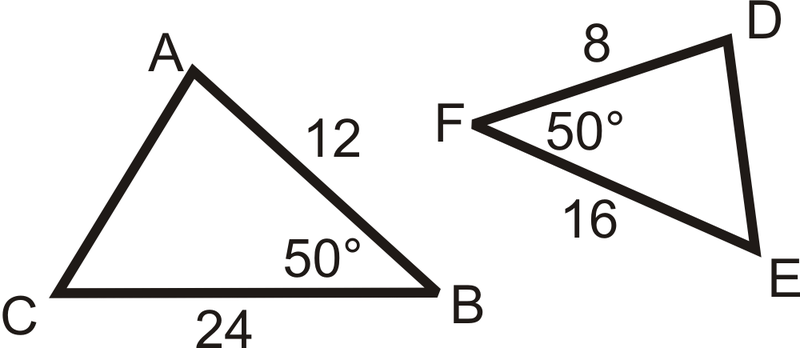
    F-D_3C5ЕС26759A40DC 1D524B1C5АФ 8864Д5Е87135063CE6F4E75D37AF4D+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Ми бачимо, що\(\angle B\cong \angle F\) і це обидва включені кути. Треба лише перевірити, щоб сторони навколо кутів були пропорційними.

    \(\begin{aligned} \dfrac{AB}{DF} &=\dfrac{12}{8}=\dfrac{3}{2} \\ \dfrac{BC}{FE}&=\dfrac{24}{16}=\dfrac{3}{2} \end{aligned}\)

    Оскільки співвідношення однакові\(\Delta ABC\sim \Delta DFE\) за теоремою подібності SAS.

    Приклад\(\PageIndex{2}\)

    Визначте, чи схожі наступні трикутники. Якщо так, напишіть теорему подібності і твердження.

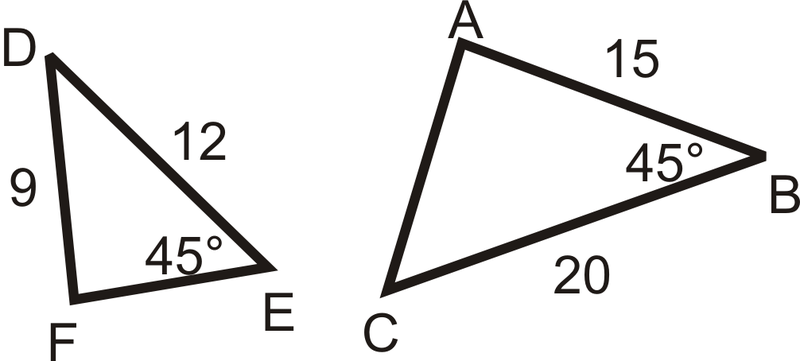
    F-д_495А286С1А8Е3А9Ф2С5297Е632КФ96Б7Е68Е4Д05Е42E277F460+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Трикутники не схожі, оскільки кут не є включеним кутом для обох трикутників.

    Приклад\(\PageIndex{3}\)

    Чи схожі два трикутника? Звідки ти знаєш?

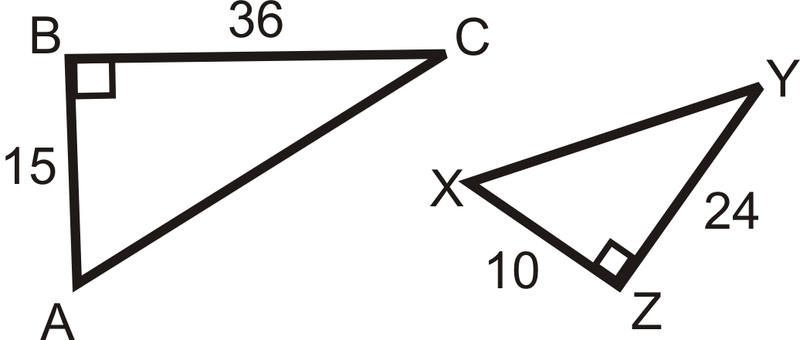
    Ф-Д_БА 359 СБ1394Е27С050Ф010Ф12Д43492С473Д92Е7Б5Ф5310Б91С3ЕЕ4А+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Ми це знаємо,\(\angle B\cong \angle Z\) тому що вони обидва прямі кути і\(\dfrac{10}{15}=\dfrac{24}{36}\). Отже,\(\dfrac{AB}{XZ}=\dfrac{BC}{ZY}\) і\(\Delta ABC\sim \Delta XZY\) по САС.

    Приклад\(\PageIndex{4}\)

    Чи є на малюнку подібні трикутники? Звідки ти знаєш?

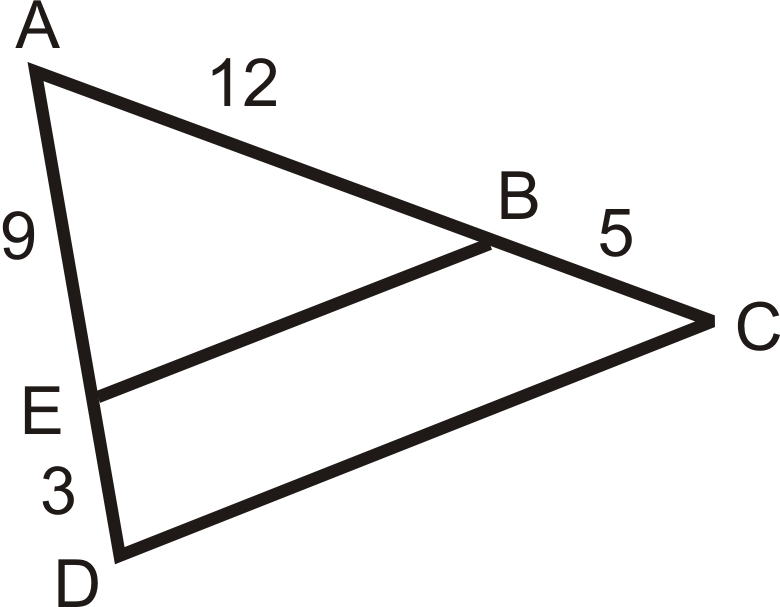
    F-д_Д2288153Б234Ф479Д5ЕЦ0Ф9 Баа221Б7А3Б806Б312С61AD4AE2C1B+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    \(\angle A\)ділиться\(\Delta EAB\) і\(\Delta DAC\), так що це конгруентно собі. Давайте подивимося, якщо\(\dfrac{AE}{AD}=\dfrac{AB}{AC}\).

    \(\begin{aligned} \dfrac{9}{9+3}&=\dfrac{12}{12+5} \\ \dfrac{9}{12}&=\dfrac{3}{4}\neq \dfrac{12}{17}\qquad \text{ The two triangles are not similar. }\end{aligned}\)

    Приклад\(\PageIndex{5}\)

    З прикладу 4, що має\(BC\) дорівнювати\(\Delta EAB\sim \Delta DAC\)?

    Рішення

    Пропорція, з якою ми закінчилися, була\(\dfrac{9}{12}=\dfrac{3}{4}\neq \dfrac{12}{17}\). AC потрібно дорівнювати 16, так що\(\dfrac{12}{16}=dfrac{3}{4}\). \(AC=AB+BC\)і\(16=12+BC\). \(BC\)повинен дорівнювати 4.

    Рецензія

    Заповніть заготовки.

    1. Якщо дві сторони в одному трикутнику - _____________ до двох сторін в інший і ________________ кути _________________, то трикутники - ______________.

    Визначте, чи схожі наступні трикутники. Якщо так, напишіть теорему подібності і твердження.

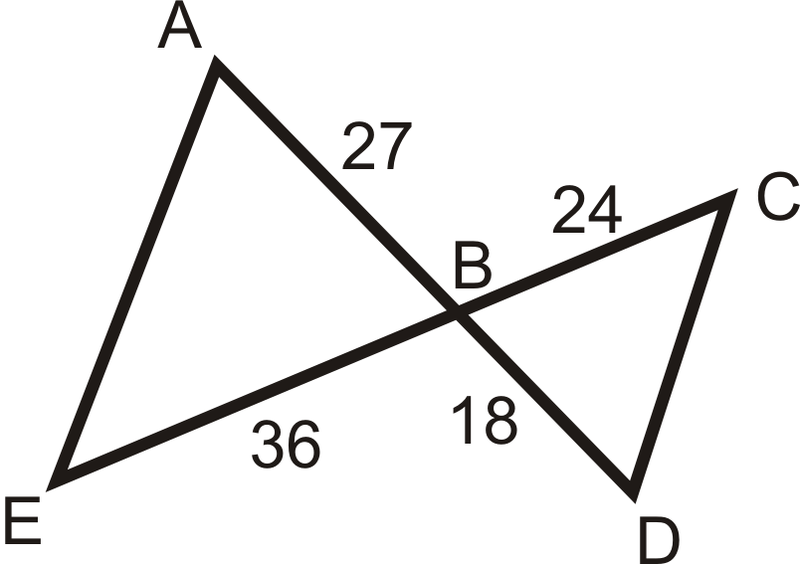
    1. F-д_А4А 69765Е7С78Ф4 КДБ880 ФДФ 5743Д9Б9А0КБЦБ Б Б А6Ф9А1Б414А52FF7+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{6}\)

    Знайдіть значення відсутньої змінної (s), яка робить два трикутника схожими.

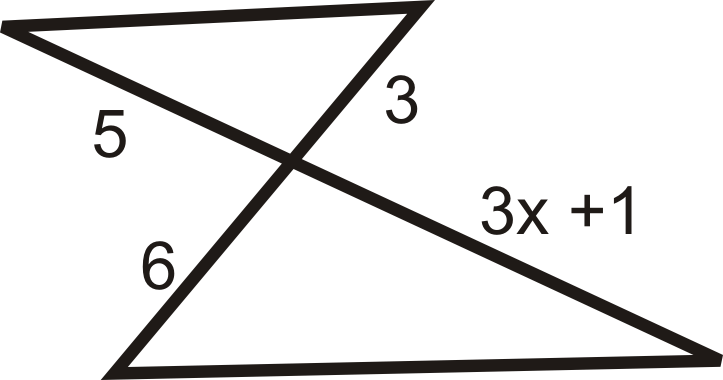
    1. F-D_0Ф9Б303КД 32Б94496979Б 576545470668 ББЭС 69Д07Б1Е9СБ Б 0Ф75Б+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
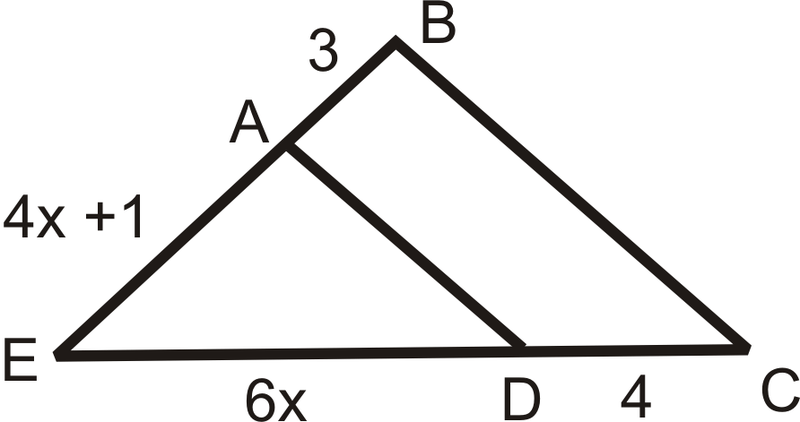
    2. F-D_323 ЕДФ 503C8CA93ДФФ 4БФ307ДФ 28Е89973C6АА696D709D5AC+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
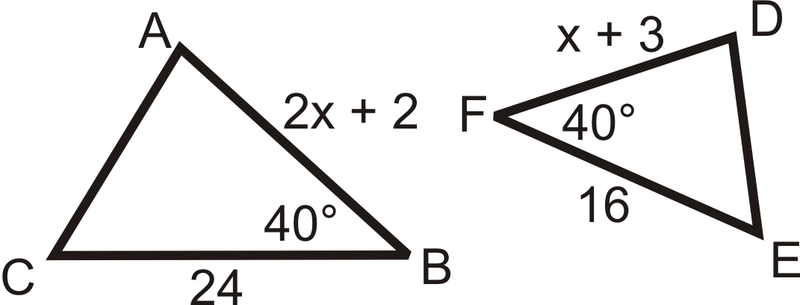
    3. F-д_0БФ 5се 4Б3576915654Е454С3АД 6ФД3С1АА19316А7Ф1С480А603Б25+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)

    Визначте, чи схожі трикутники. Якщо так, напишіть теорему подібності і твердження.

    1. \(\Delta ABC\)являє собою прямокутний трикутник з ніжками, які вимірюють 3 і 4. \(\Delta DEF\)являє собою прямокутний трикутник з ніжками, які вимірюють 6 і 8.
    2. \(\Delta GHI\)прямокутний трикутник з катетом, який вимірює 12 і гіпотенузою, яка вимірює 13. \(\Delta JKL\)являє собою прямокутний трикутник з ніжками, які вимірюють 1 і 2.
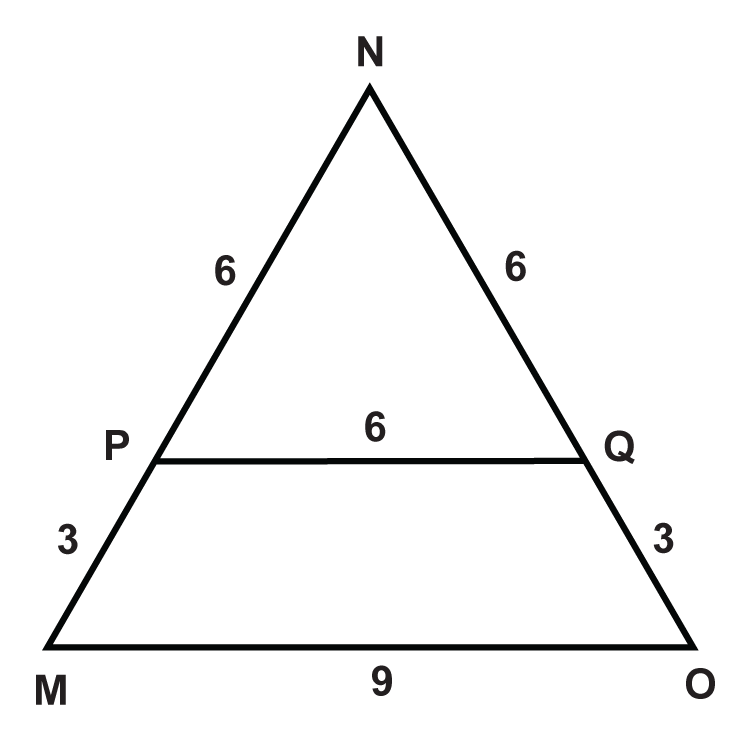
    3. F-D_2873 АФ 3Д8А3972А1Ф262545А 5БД89Е875Б215Б5194Д146Ф0Е8А0+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
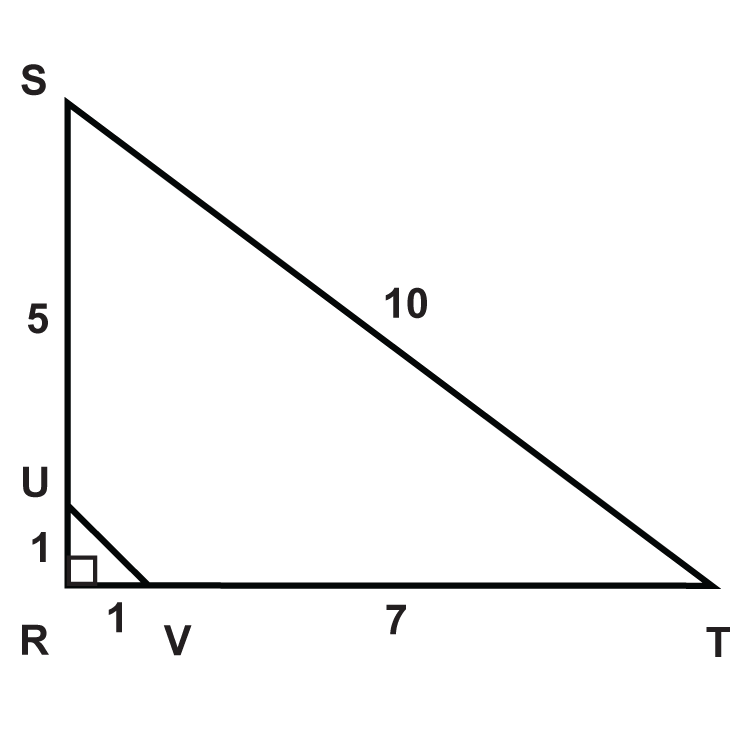
    4. F-д_2c00c88531a025e29492cd7a0671548293E34155b54DE673b673424E+зображення_крихіткий+зображення_крихіткий_png
      Малюнок\(\PageIndex{11}\)
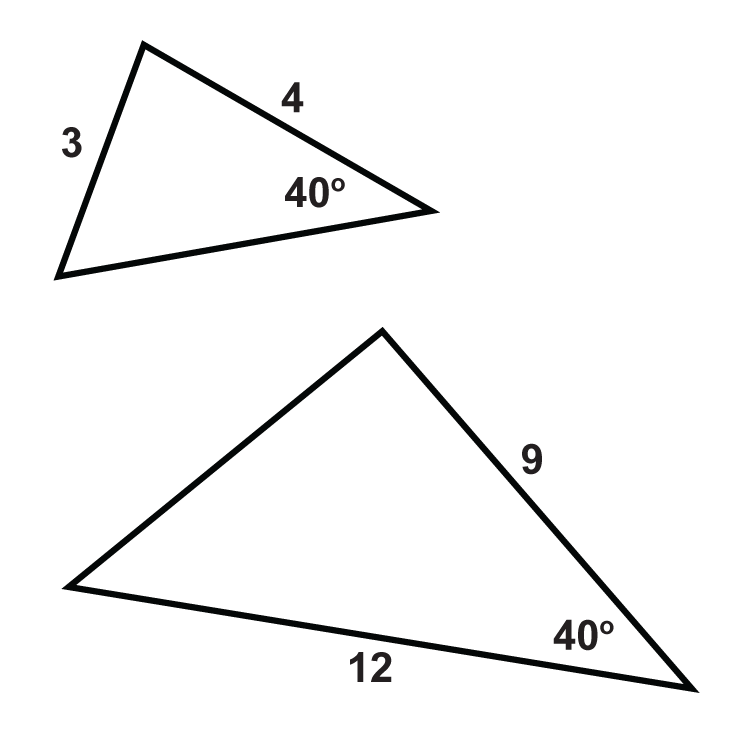
    5. F-D_87E6D837B5FFF24 Асе0 Каб 92Б Ае 3БА 30Б137 Баф БД4275146Б1Е0207+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
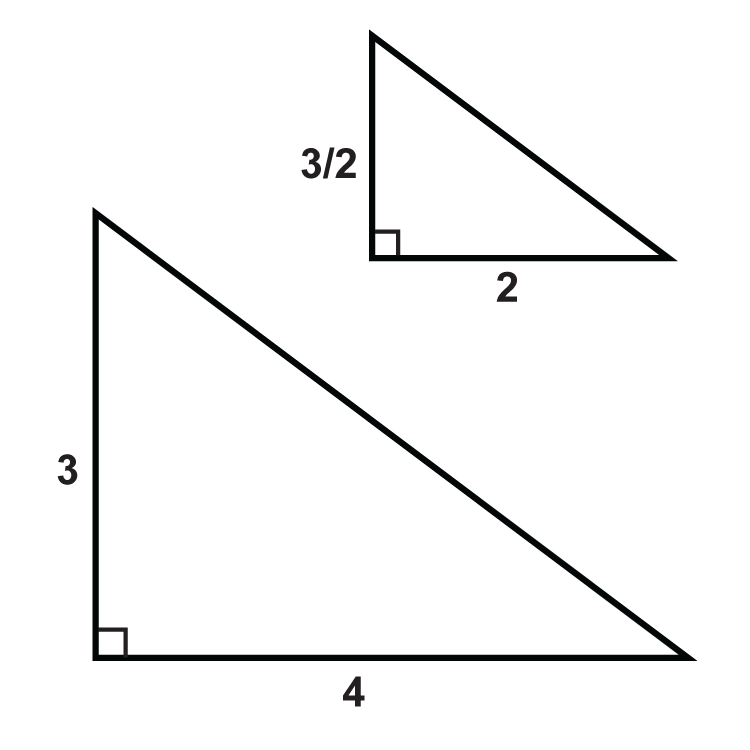
    6. F-D_6E 06176318 ФД2С3Е541 С67А29А65БАЕ61БФ8С181ДД056ДДА 3АЦ71+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
    7. \(\overline{AC}=3\)

    \(\overline{DF}=6\)

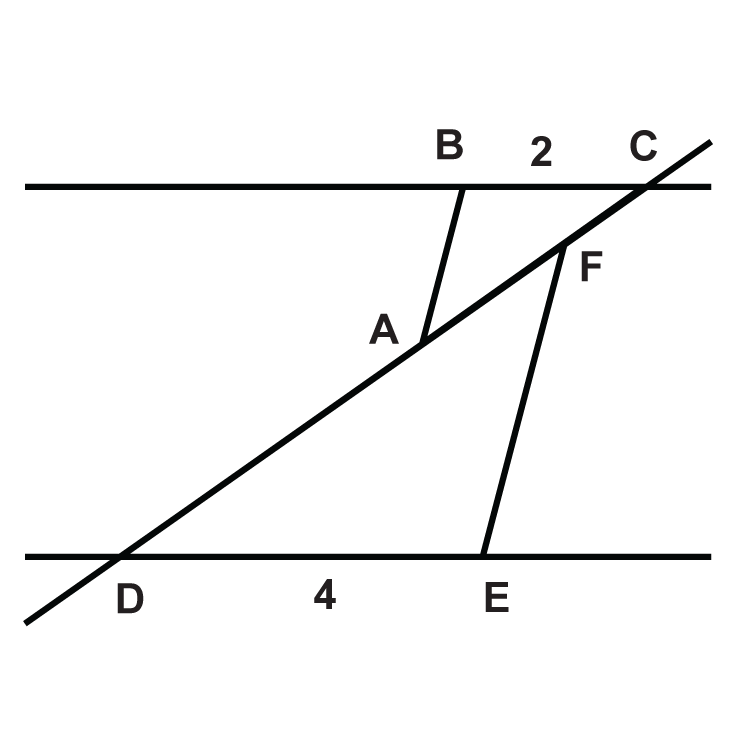
    Ф-д_а479Ф34Б11071 С9Е3Ф33Д5С4232Ф51Д562Е1Е1ААА5ЕФ+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{14}\)
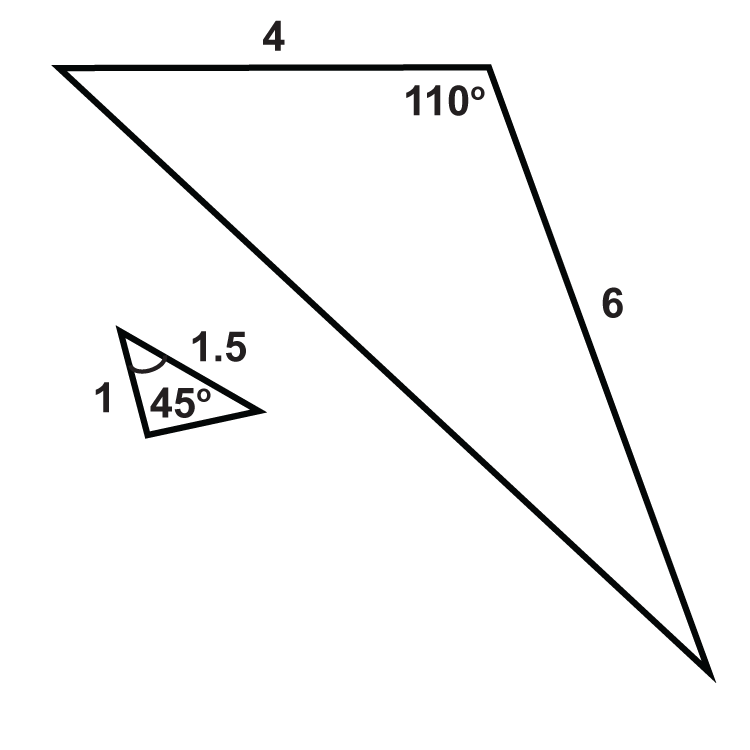
    1. F-д_16БКА2Е2Б112Б6705 АС 3486634Б8Е1Д11159781Ф0А6ФЕ9Е8ЕДК85+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
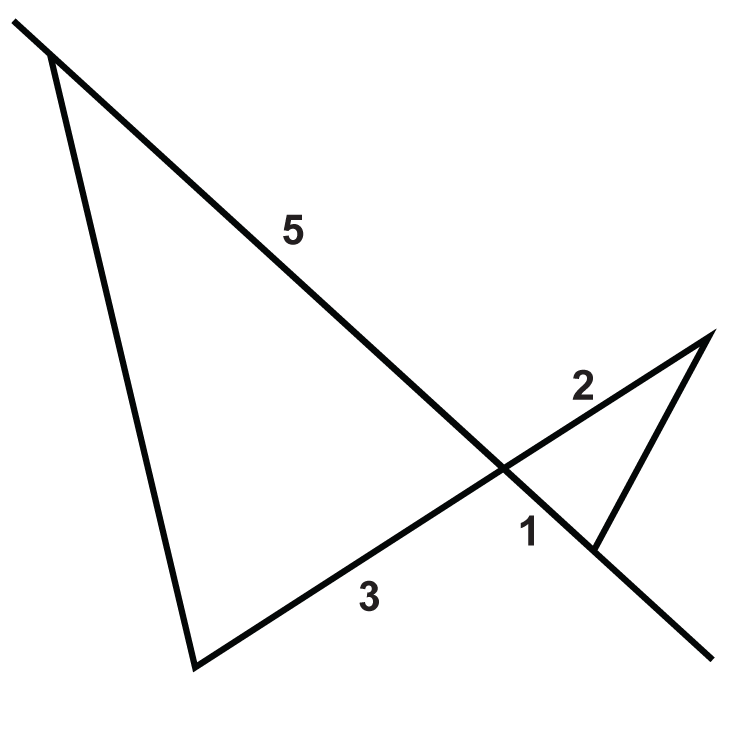
    2. Ф-Д_7Д5Ф10 ФБ 63Д049БЦФ 3Ф7АФ 231 АЦБ6Д2647Д4 Кад 32ЦАЕ07ДК8123Б+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
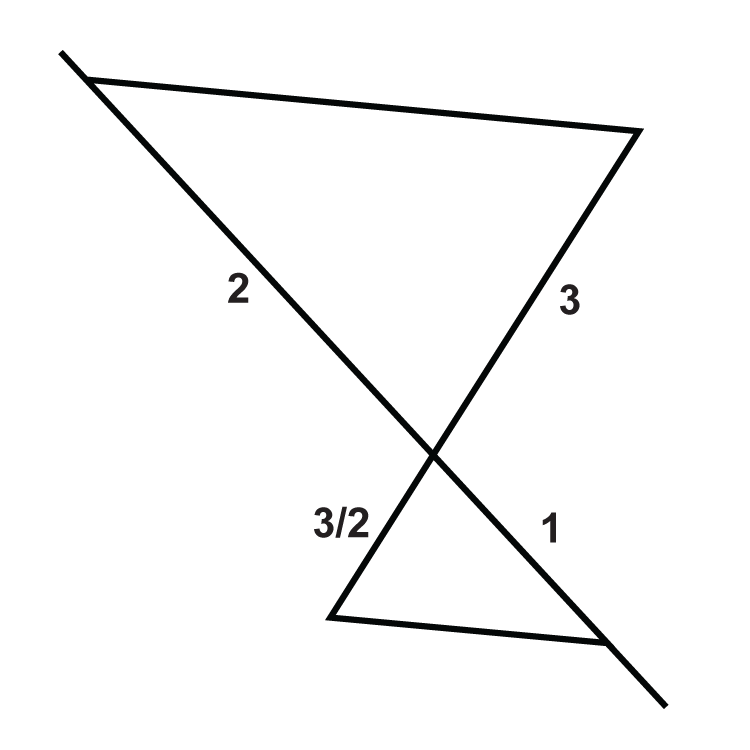
    3. F-д_Е0Е0С83568Ф9АД 896342Б3407АФ0Б 31Б005202E1F29642827735460+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\ (\ Індекс сторінки {17}\

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 7.7.

    Ресурси

    Лексика

    Термін Визначення
    Постулат подібності AA Якщо два кути в одному трикутнику збігаються з двома кутами в іншому трикутнику, то два трикутника схожі.
    Конгруентний Конгруентні фігури ідентичні за розміром, формою і мірою.
    Дилатація Зменшити або збільшити цифру відповідно до масштабного коефіцієнта - це розширення.
    SAS SAS означає сторону, кут, сторону, і відноситься до того, що дві сторони і включений кут трикутника відомі.
    Теорема подібності SAS Теорема подібності SAS стверджує, що якщо дві сторони в одному трикутнику пропорційні двом сторонам в іншому трикутнику, а включений кут в обох є конгруентними, то два трикутники схожі.
    Трансформація подібності Перетворення подібності - це одне або кілька жорстких перетворень з подальшим розширенням.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Конгруентні та подібні трикутники

    Діяльність: Питання обговорення подібності SAS

    Навчальні посібники: Посібник з вивчення схожості полі

    Практика: Схожість SAS

    Реальний світ: схожість трикутника