7.8: Схожість SSS

Трикутники схожі, якщо відповідні їх сторони пропорційні.

Теорема про подібність SSS

За визначенням два трикутника схожі, якщо всі відповідні їм кути конгруентні, а відповідні їм сторони пропорційні. Не обов'язково перевіряти всі кути і сторони, щоб визначити, чи схожі два трикутника. Насправді, якщо ви знаєте лише, що всі сторони пропорційні, достатньо інформації, щоб знати, що трикутники схожі. Це називається теоремою подібності SSS.

Теорема подібності SSS: Якщо всі три пари відповідних сторін двох трикутників пропорційні, то два трикутники схожі.

Малюнок$\PageIndex{1}$

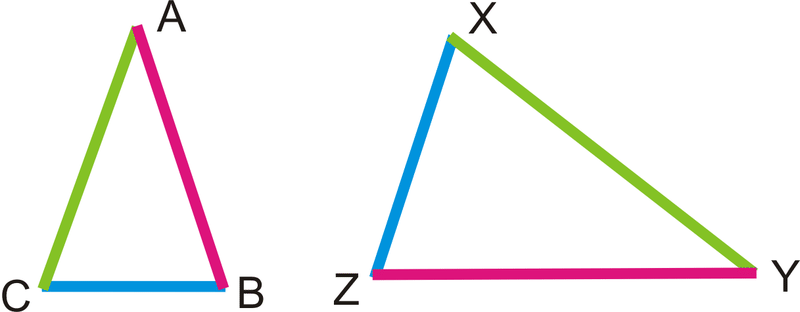
Якщо$\dfrac{AB}{YZ}=\dfrac{BC}{ZX}=\frac{AC}{XY}$, то$\Delta ABC\sim \Delta YZX$.

Що робити, якщо вам дали пару трикутників і довжини сторін для всіх трьох їх сторін? Як ви могли б використовувати цю інформацію, щоб визначити, чи два трикутники схожі?

Для прикладів 1 і 2 використовуйте наступну діаграму:

Малюнок$\PageIndex{2}$

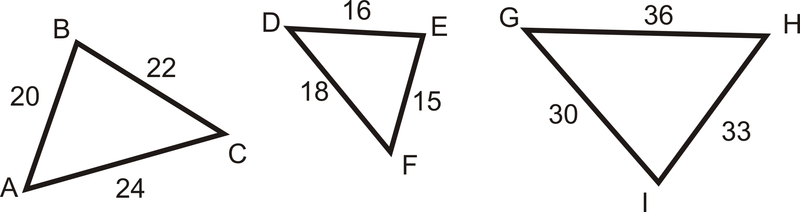
Приклад$\PageIndex{1}$

Є$\Delta DEF\sim \Delta GHI$?

Є$\dfrac{15}{30}=\dfrac{16}{33}=\dfrac{18}{36}$?

Рішення

$\dfrac{15}{30}=\dfrac{1}{2}$,$\dfrac{16}{33}=\dfrac{16}{33}$, і$\dfrac{18}{36}=\dfrac{1}{2}$. $\dfrac{1}{2}\neq \dfrac{16}{33}$,$\Delta DEF$ не схожий на$\Delta GHI$.

Приклад$\PageIndex{2}$

Є$\Delta ABC\sim \Delta GHI$?

Є$\dfrac{20}{30}=\dfrac{22}{33}=\dfrac{24}{36}$?

Рішення

$\dfrac{20}{30}=dfrac{2}{3}$,$\dfrac{22}{33}=\dfrac{2}{3}$, і$\dfrac{24}{36}=\dfrac{2}{3}$. Всі три співвідношення звести до$\dfrac{2}{3}$,$\Delta ABC\sim \Delta GHI$.

Приклад$\PageIndex{3}$

Визначте, чи схожі наступні трикутники. Якщо так, поясніть чому і напишіть заяву подібності.

Малюнок$\PageIndex{3}$

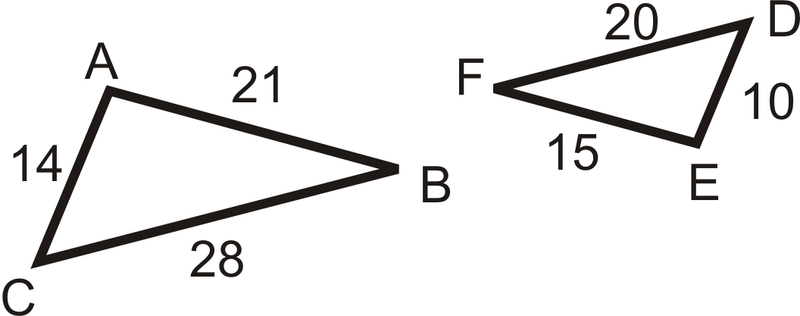
Рішення

Нам потрібно буде знайти співвідношення для відповідних сторін трикутників і подивитися, чи всі вони однакові. Почніть з найдовших сторін і працюйте вниз до найкоротших сторін.

$\begin{aligned} \dfrac{BC}{FD}&=\dfrac{28}{20}=\dfrac{7}{5} \\ \dfrac{BA}{FE}&=\dfrac{21}{15}=\dfrac{7}{5} \\ \dfrac{AC}{ED}&=\dfrac{14}{10}=\dfrac{7}{5}\end{aligned}$

Оскільки всі співвідношення однакові,$\Delta ABC\sim \Delta EFD$ по теоремі подібності ССС.

Приклад$\PageIndex{4}$

Знайти$x and \(y, such that \(\Delta ABC\sim \Delta DEF$.

Малюнок$\PageIndex{4}$

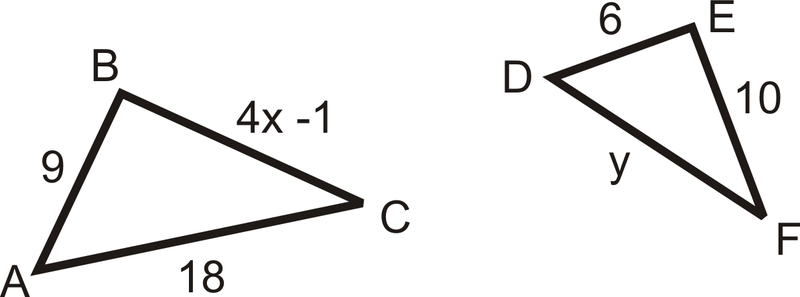
Рішення

Відповідно до заяви про подібність, відповідними сторонами є:$\dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}$. Підставляючи те, що ми знаємо, ми маємо$\dfrac{9}{6}=\dfrac{4x−1}{10}=\dfrac{18}{y}$.

\ (\ почати {вирівняні}
\ розриву {9} {6} &=\ гідророзриву {4 x-1} {10} &\ гідророзриву {9} {6} &=\ гідророзриву {18} {y}\\
9 (10) &=6 (4 x-1) & 9 y=18 (6)\
90 &= 24 х-6 & 9 y=108\
96 &=24 х & y=12\\
x &= 4 &
\ end {вирівняний}\)

Приклад$\PageIndex{5}$

Визначте, чи схожі наступні трикутники. Якщо так, поясніть чому і напишіть заяву подібності.

Малюнок$\PageIndex{5}$

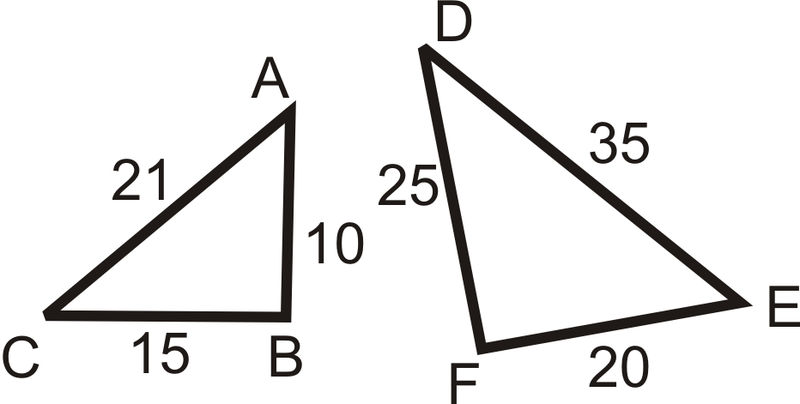
Рішення

Нам потрібно буде знайти співвідношення для відповідних сторін трикутників і подивитися, чи всі вони однакові. Почніть з найдовших сторін і працюйте вниз до найкоротших сторін.

$\begin{aligned} \dfrac{AC}{ED}&=\dfrac{21}{35}=\dfrac{3}{5} \\ \dfrac{BC}{FD}&=\dfrac{15}{25}=\dfrac{3}{5} \\ \dfrac{AB}{EF}&=\dfrac{10}{20}=\dfrac{1}{2} \end{aligned}$

Так як співвідношення не всі однакові, трикутники не схожі.

Рецензія

Заповніть заготовки.

1. Якщо всі три сторони в одному трикутнику розташовані __________________ до трьох сторін в іншому, то два трикутника схожі.
2. Два трикутника схожі, якщо відповідні сторони _____________.

Використовуйте наступну схему для питань 3-5. Діаграма полягає в масштабі.

Малюнок$\PageIndex{6}$

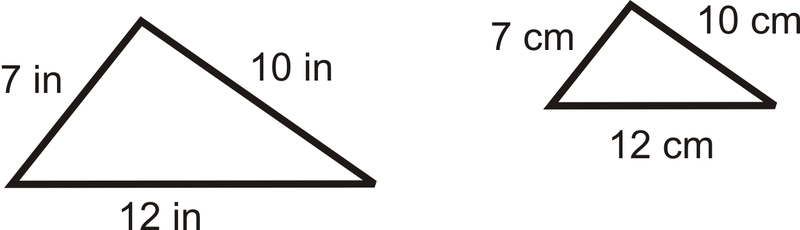
3. Чи схожі два трикутника? Поясніть свою відповідь.
4. Чи є два трикутника конгруентними? Поясніть свою відповідь.
5. Який масштабний коефіцієнт для двох трикутників?

Заповніть пропуски в відомостях нижче. Використовуйте схему зліва.

Малюнок$\PageIndex{7}$

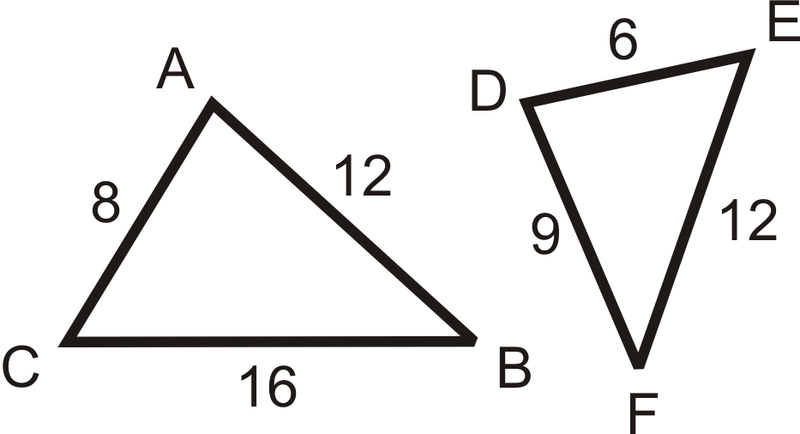
6. $\Delta ABC\sim \Delta _____$
7. $\dfrac{AB}{?}=\dfrac{BC}{?}=\dfrac{AC}{?}$
8. $\Delta ABC$Якби була висота$AG=10$, якою була б довжина висоти$\overline{DH}$?
9. Знайдіть периметр$\Delta ABC$ і$\Delta DEF$. Знайдіть співвідношення периметрів.

Використовуйте діаграму праворуч для питань 10-15.

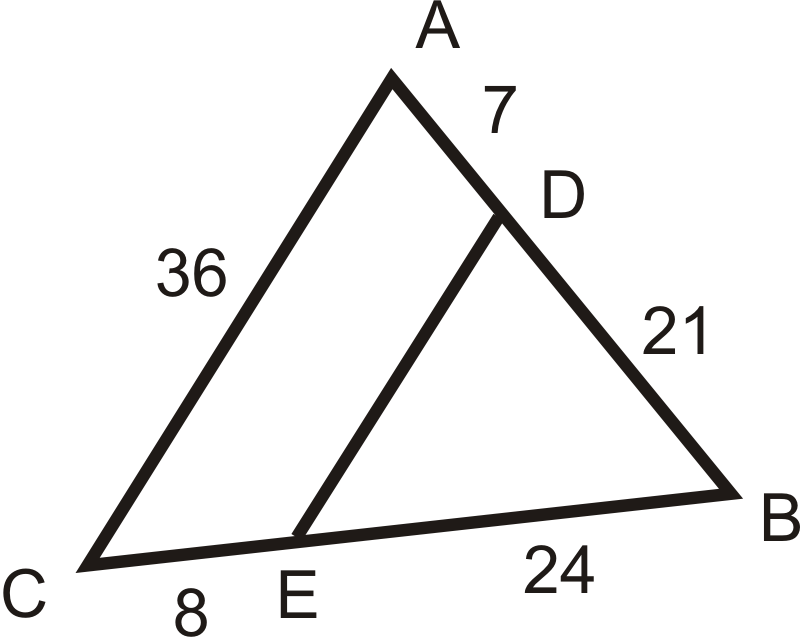Малюнок\(\PageIndex{8}\)

10. $\Delta ABC\sim \Delta _____$
11. Чому два трикутника схожі?
12. Знайти$ED$.
13. $\dfrac{BD}{?}=\dfrac{?}{BC}=\dfrac{DE}{?}$
14. Це$\dfrac{AD}{DB}=\dfrac{CE}{EB}$ правда?
15. Це$\dfrac{AD}{DB}=\dfrac{AC}{DE}$ правда?

Знайдіть значення відсутньої змінної (s), яка робить два трикутника схожими.

16. 

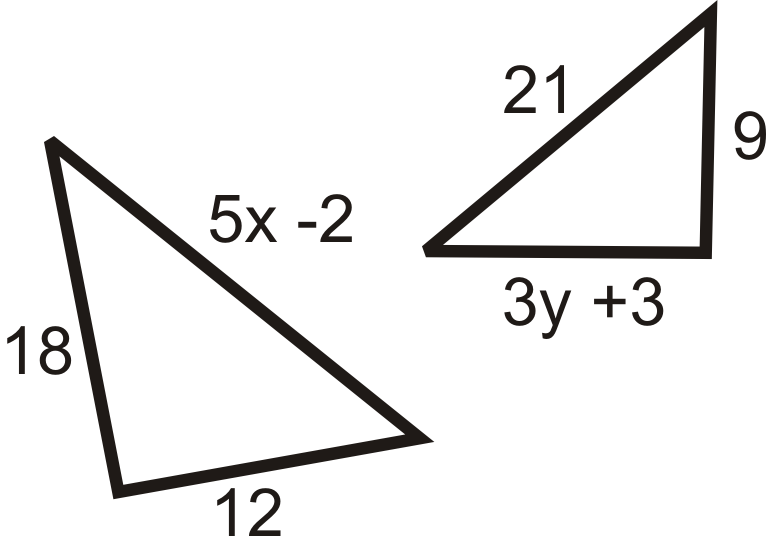
    Малюнок$\PageIndex{9}$

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 7.6.

Ресурси

Лексика

Термін	Визначення
Теорема подібності AAA	Теорема подібності AAA стверджує, що якщо всі три пари відповідних сторін двох трикутників пропорційні, то два трикутника схожі.
Конгруентний	Конгруентні фігури ідентичні за розміром, формою і мірою.
Дилатація	Зменшити або збільшити цифру відповідно до масштабного коефіцієнта - це розширення.
Співвідношення	Співвідношення - це порівняння двох величин, які можуть бути записані у вигляді дробу, з двокрапкою або зі словом «до».
ССС	SSS означає сторону, сторону, сторону і відноситься до того, що всі три сторони трикутника відомі в задачі.
Жорстке перетворення	Жорстке перетворення - це перетворення, яке зберігає відстань і кути, воно не змінює розмір або форму фігури.

Додаткові ресурси

Інтерактивний елемент

Відео: Конгруентні та подібні трикутники

Діяльність: Питання обговорення подібності SSS

Навчальні посібники: Посібник з вивчення схожості полі

Практика: Схожість SSS

Реальний світ: Божевільна ковдра