Skip to main content
LibreTexts - Ukrayinska

7.5: Непряме вимірювання

  1. Last updated
  2. Save as PDF
  • Page ID
    54685

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Знайдіть довжини, використовуючи пропорції аналогічних трикутників.

    Невідомі міри аналогічних цифр

    F-D_93FACDA 3C0DABBE641E19F34672 ББК 8Б04Д6С Бусина ADFBA34F5A42A6B9+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_jpg
    Малюнок\(\PageIndex{1}\)

    Батько Шелбі - колишній олімпійський плавець. Він любить плавати, але він не може побудувати басейн олімпійського розміру на задньому дворі, тому що у нього немає місця. Він вирішує побудувати менший басейн, який схожий з розмірами олімпійського басейну. Олімпійський басейн має довжину 50 метрів і ширину 25 метрів. Його басейн має довжину 25 метрів. Яка ширина його басейну?

    У цьому понятті ви дізнаєтеся, як знайти невідомі мірки подібних фігур.

    Пошук невідомих мір аналогічних фігур

    Якщо ви знаєте довжину сторони на одній фігурі, ви можете скористатися масштабним коефіцієнтом, щоб знайти міру відповідної сторони на аналогічній цифрі. Давайте подивимося, як це працює.

    Сторона a в трикутнику ABC відповідає стороні x у меншому трикутнику XYZ. Сторона x має довжину 4 метри, а коефіцієнт масштабу - 6. Що таке міра сторони а?

    Вам сказали, що дві сторони, a і x, відповідають маленьким трикутником і великим. Сторона x має довжину 4 метри, а масштабний коефіцієнт говорить вам, що сторона a буде в шість разів довшою. Давайте випишемо це і вирішимо.

    \(\text{side} x \times \text{ scale factor }=\text{ side }\: a\)

    \(4\times 6=\text{ side a }\)

    \(24 \text{ m }=\text{ side a }\)

    Сторона а повинна мати довжину 24 метри.

    Ви можете перевірити, встановивши співвідношення, яке порівнює довжини двох сторін. Якщо коефіцієнт масштабування дорівнює 6, значить, ваша робота точна.

    \(\dfrac{a}{x}=\dfrac{24}{4}=6\)

    Іноді ви можете з'ясувати відсутні довжини сторін, дивлячись на дані заходи. Завжди дивіться на діаграму фігур і дивіться, чи зможете ви визначити відсутню довжину без вимірювання.

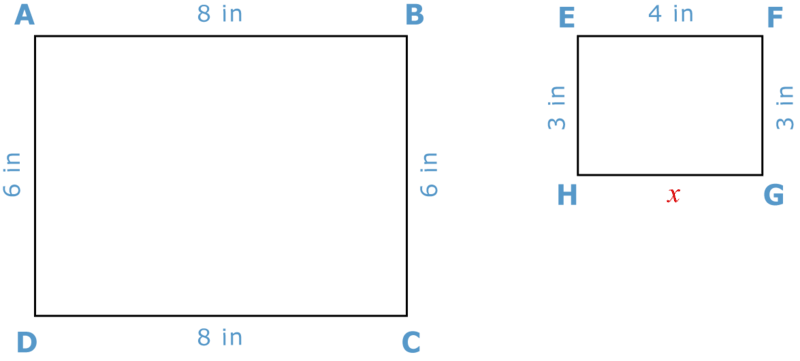
    F-D_C9420874D4665C1d2573 ДК 56С438 BA0784671672E2D6A31C9A12B44+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{2}\)

    Подивіться на ці два прямокутника. Спочатку подивіться і подивіться, чи зможете ви з'ясувати взаємозв'язок між двома фігурами. Для цього ви порівняєте довжини сторін кожної частини двох фігур.

    Потрібно з'ясувати вимір сторони GH в другому прямокутнику.

    Ви можете бачити, що вимірювання у другому прямокутнику вдвічі більші, ніж вимірювання в першому. Крім того, ви знаєте, що протилежні сторони прямокутника є конгруентними. Тому відсутня довжина сторони дорівнює 4.

    Подібні цифри, пов'язані масштабним коефіцієнтом, часто можна побачити на картах, архітектурних кресленнях і діаграмах. У більшості цих випадків коефіцієнт масштабу задається таким чином, щоб ви знали, як збільшити елементи на кресленні до їх реальних розмірів. Погляньте на план поверху нижче. На ній показано, де розташована меблі у вітальні.

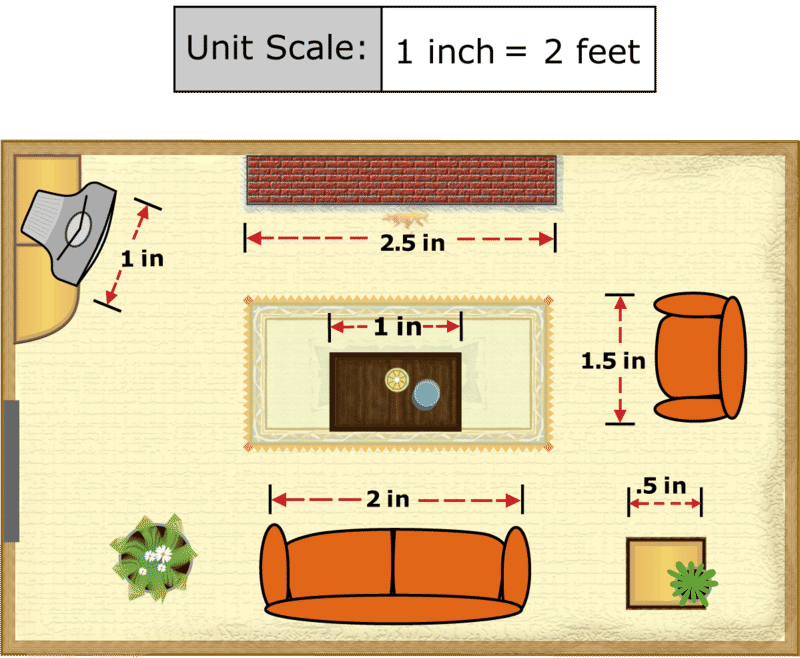
    F-д_0Б74Б1026Ф16701ДАА17А3Б56Ф7 ФА2824141Е313054Б5Д34476ЦБФ1+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Це говорить вам, що один дюйм на кресленні дорівнює двом футам в фактичному розмірі. Тому, якщо ви знаєте розмір в дюймах будь-якого об'єкта в плані поверху, ви можете знайти його фактичний розмір в футах. Давайте спробуємо.

    Знайдіть диван на плані поверху, а потім знайдіть його довжину в дюймах. Диван в плані поверху має довжину 2 дюйми. Це все одно, що знати довжину однієї сторони в подібній фігурі. Тепер використовуйте масштабний коефіцієнт так, як ви б знайшли довжину відповідної сторони на аналогічній фігурі (в цьому випадку «відповідна сторона» - це фактичний диван). Просто помножте відому довжину на коефіцієнт масштабування:

    \(\text{ sofa drawing }\times \text{ scale factor }=\text{ actual sofa size }\)

    \(2\text{ inches }\times 2=4 \text{ feet }\)

    Диван довжиною 4 фути.

    Далі розрахуємо реальну довжину каміна. За допомогою лінійки виміряти камін на кресленні. Він має довжину 2,5 дюйма. Помножте це на масштабний коефіцієнт, щоб знайти довжину в футах.

    \(\text{ fireplace drawing }\times \text{ scale factor }=\text{ actual fireplace length }\)

    \(2.5\text{ inches}\times 2=5 \text{ feet }\)

    Реальна довжина каміна - 5 футів.

    Ви також можете змінити процес, щоб взяти фактичний розмір і зменшити його.

    Приклад\(\PageIndex{1}\)

    Раніше вам давали проблему з приводу батька Шелбі і його басейну.

    Він будує басейн, схожий на олімпійський басейн. Олімпійський басейн має довжину 50 метрів і ширину 25 метрів. Якщо його басейн має довжину 25 метрів, яка ширина його басейну?

    Рішення

    Для початку створіть рівняння, яке можна використовувати для вирішення ширини його басейну.

    \(\dfrac{50}{25}=\dfrac{25}{x}\)

    Далі перехресне множиться.

    \(50x=625\)

    Потім розділіть обидві сторони рівняння на 50.

    \(x= 12.5\)

    Відповідь полягає в тому, що його басейн має ширину 12,5 метрів.

    Приклад\(\PageIndex{2}\)

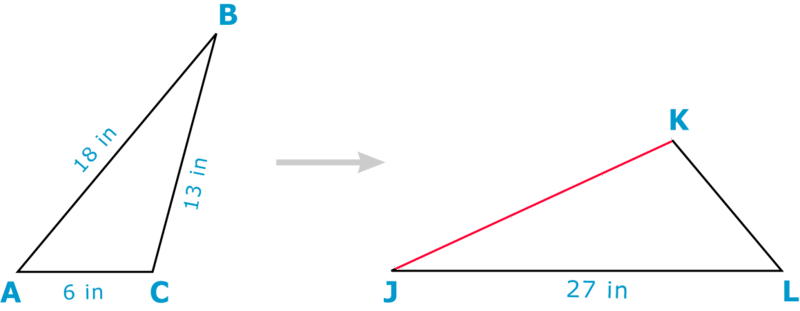
    Скористайтеся масштабним коефіцієнтом аналогічних цифр нижче, щоб знайти міру KJ.

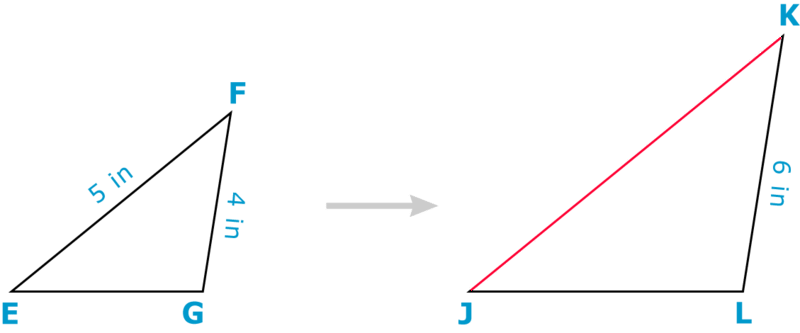
    F-д_ФД546Д166EB9C5E60D87167231 ББ88 ФБ96Е2С8713ДФ6Е45616358DCD+зображення_крихіткий+зображення_крихітковий_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Спочатку встановіть пропорцію, щоб вирішити для відсутньої сторони.

    \(\dfrac{KJ}{5}=\dfrac{6}{4}\)

    Ця пропорція пишеться так, щоб відповідні сторони утворювали два співвідношення пропорції. Можна сказати, що\(KJ\) невідомо в цій пропорції.

    Далі перехресне множиться.

    \(\begin{aligned} KJ\times 4&=4KJ \\ 5\times 6&=30 \\ 4KJ&=30\end{aligned}\)

    Потім вирішити рівняння для KJ, розділивши обидві сторони рівняння на 4.

    \(\begin{aligned} 30\divide 4&=7.5 \\ KJ&=7.5 \end{aligned}\)

    Відповідь полягає в тому, що довжина сторони\(KJ\) дорівнює 7,5.

    Приклад\(\PageIndex{3}\)

    Кріс робить малюнок своєї школи та майданчиків навколо неї. Баскетбольний майданчик довжиною 75 футів і шириною 40 футів. Якщо Кріс використовує масштабний коефіцієнт, при якому 1 дюйм дорівнює 10 футам, які повинні бути розміри баскетбольного майданчика на його кресленні?

    F-д_6е8417 Ед 9667E1Б1Ф74044488145839256472E100109C8E5497F0117+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{5}\)

    Рішення

    Для початку напишіть інформацію, яку ви знаєте.

    Фактичний розмір баскетбольного майданчика і масштабний коефіцієнт Кріс використовує для свого малюнка.

    Далі встановіть рівняння, щоб знайти довжину, яку повинен намалювати Кріс.

    \(\begin{aligned} \text{ drawing length }\times \text{ scale factor }=\text{ actual basketball court length } \\ \text{ drawing length } \times 10=75 feet \\ \text{ drawing length }&=75\divide 10 \\ \text{ drawing length }&=7.5 \text{ inches }\end{aligned}\)

    Довжина баскетбольного майданчика в кресленні Кріса повинна бути 7,5 дюймів.

    Потім скористайтеся тим самим процесом, щоб знайти ширину, яку повинен намалювати Кріс.

    \(\begin{aligned} \text{ drawing width } \times \text{ scale factor }=\text{ actual basketball court width }\\ \text{ drawing width } \times 10=40 \text{ feet } \\ \text{ drawing width }=40\divide 10 \\ \text{ drawing width }=4\text{ inches } \end{aligned}\)

    Відповідь полягає в тому, що Кріс повинен представляти баскетбольний майданчик як прямокутник розміром 7,5 на 4 дюйма на своєму кресленні.

    Приклад\(\PageIndex{4}\)

    Вирішити для\(x\).

    \(\dfrac{3}{4}=\dfrac{x}{12}\)

    Рішення

    Спочатку перехресне множення.

    \(4x = 36\)

    Далі розділіть обидві сторони рівняння на 4.

    \(x = 9\)

    Потім викладіть розчин.

    9

    Відповідь полягає в тому, що\(x\) дорівнює 9.

    Приклад\(\PageIndex{5}\)

    Вирішити для\(x\).

    \(\dfrac{3}{6}=\dfrac{1}{x}\)

    Рішення

    Спочатку перехресне множення.

    \(3x = 6\)

    Далі розділіть обидві сторони рівняння на 3.

    \(x = 2\)

    Потім викладіть розчин.

    2

    Відповідь полягає в тому, що\(x\) дорівнює 2.

    Рецензія

    Вирішіть кожну проблему.

    1. Сторона\(m\) в трикутнику\(LMN\) відповідає стороні c в меншому трикутнику\(BCD\). Сторона m має довжину 12 см, а масштабний коефіцієнт - 4. Що таке міра сторони c?
    2. Сторона\(q\) в трикутнику\(PQR\) відповідає стороні y в меншому трикутнику\(XYZ\). Сторона y має довжину 8 дюймів, а масштабний коефіцієнт - 7. Що таке міра сторони q?

    Вирішіть кожну пропорцію для відсутньої довжини сторони.

    1. \(\dfrac{7}{10}=\dfrac{x}{30}\)
    2. \(\dfrac{1.5}{3}=\dfrac{x}{6}\)

    Тепер використовуйте масштабний коефіцієнт, щоб створити нове співвідношення.

    1. \(\dfrac{1}{3}\), коефіцієнт масштабування 4
    2. \(\dfrac{8}{5}\), коефіцієнт масштабування 5
    3. \(\dfrac{9}{3}\), коефіцієнт масштабування 3
    4. Знайдіть масштабний коефіцієнт аналогічних цифр нижче, а потім скористайтеся ним, щоб знайти міру LO\).
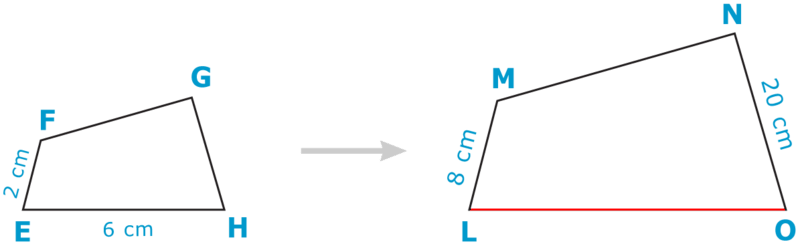
    F-D_6 АББ 802А66Д88Б3 АБ 114Д2 ЕЕЕЦЕ7Д71Б44БК 134Ф57БК5А ЕЕА4 До н.е+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)
    1. Використовуйте масштабний коефіцієнт аналогічних цифр нижче, щоб знайти міру\(JK\).
    Ф-д_Е5А3А0А 37С65Е6ФК 2915Е4515Ф 9859Ф4Ф1132 ФК15Е7АФ1456CF8E+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Використовуйте карту нижче і лінійку, щоб відповісти на наступні питання.

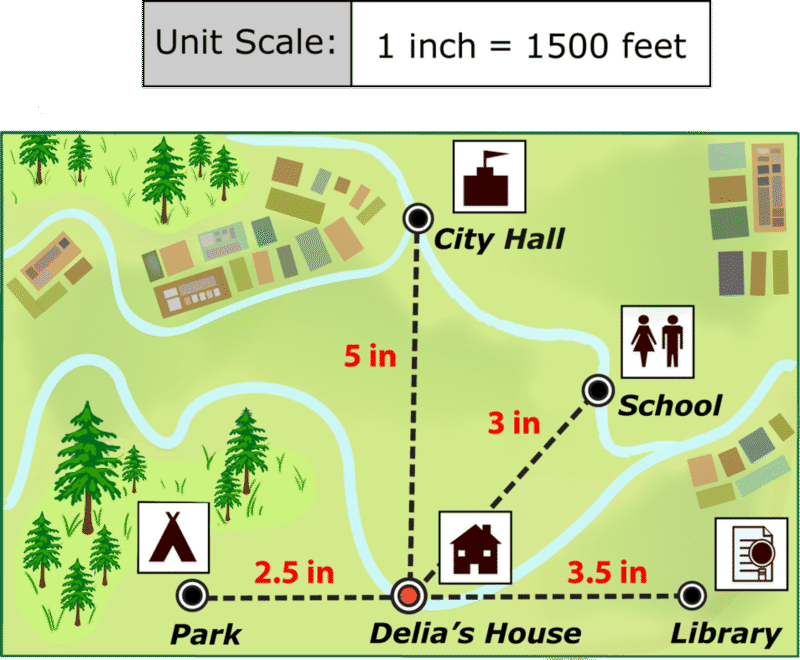
    F-D_A502E9E29823C558CA8564 CFBF БФ 4ФА08Ф1Д8766A8CE216D70D75+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)
    1. Як далеко живе Делія від своєї школи?
    2. Як далеко від бібліотеки до парку?
    3. Як далеко Делia живе від Мері-Холла?
    4. Делія намалювала ще одну точку, щоб показати поліцейську дільницю на своїй карті. Вона намалювала його на відстані 1,5 дюймів від мерії. Яка реальна відстань між поліцейською дільницею та мерією?
    5. Як далеко живе Delia від парку?
    6. Як далеко вона живе від бібліотеки?
    7. Що найдалі, що Делія подорожує до будь-якого пункту на своїй карті?

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.15.

    Ресурси

    Лексика

    Термін Визначення
    Непряме вимірювання Непряме вимірювання - це процес використання характеристик подібних трикутників для вимірювання відстаней.
    Масштабний коефіцієнт Масштабний коефіцієнт - це відношення масштабу до вихідного або фактичного виміру, написаного в найпростішій формі.
    Схожі Дві фігури схожі, якщо вони мають однакову форму, але не обов'язково однакового розміру.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Конгруентні та подібні трикутники

    Практика: Непряме вимірювання

    Реальний світ: Могутні вимірювання