7.4: Відповідні частини аналогічних фігур
- Page ID
- 54660
Визначте відповідні довжини сторін та вимірювання кута в аналогічних цифрах.

У Марії є мистецький проект, який належить до школи. Вона вирішує зробити невелику копію своєї спальні. Вона починає з вимірювання кутів своєї спальні, потім малює подібні фігури. Більша фігура представляє її спальню, а менша фігура - її репліка.
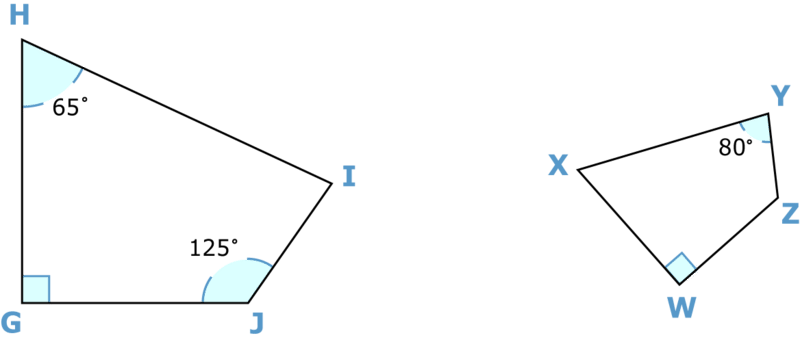
Її двері спальні розташована посеред\(\overline{IJ}\). Для її репліки двері необхідно розташувати посередині відповідної сторони. Яка сторона репліки відповідає\(\overline{IJ}\)?
У цьому понятті ви дізнаєтеся про відповідні сторони подібних фігур.
Відповідні частини аналогічних фігур

Трикутник ABC схожий на трикутник DEF. Це означає, що, хоча вони мають однакову форму, вони не мають однакового розміру. Насправді існує взаємозв'язок між відповідними частинами трикутника.
Довжина сторін відповідає, навіть якщо вони не є конгруентними. Використовуйте символ для подібного (»\(\sim\) «), щоб показати зв'язок між відповідними сторонами двох трикутників.
\(\overline{AB}\sim \overline{DE}\)
\(\overline{BC}\sim \overline{EF}\)
\(\overline{AC}\sim \overline{DF}\)
Приклад\(\PageIndex{1}\)
Раніше вам давали проблему про Марію і її спальні.
Вона робить репліку своєї спальні для свого художнього класу. Вона малює дві подібні фігури, щоб переконатися, що вона розміщує все в правильному положенні.
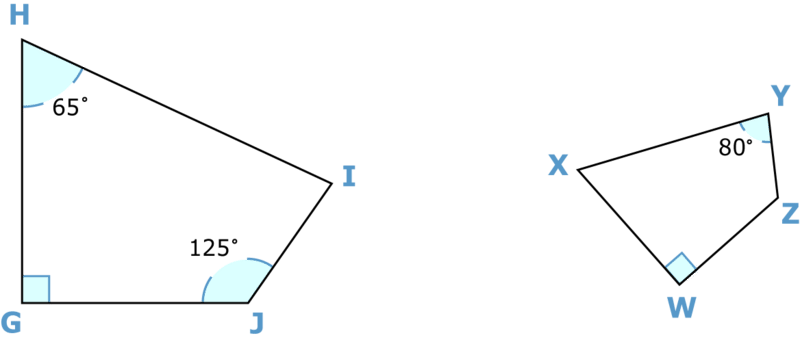
Рішення
Їй потрібно розмістити двері своєї спальні посередині тієї сторони, яка відповідає\(\overline{IJ}\). Яка сторона відповідає\(\overline{IJ}\)?
Спочатку поверніть другу фігуру так, щоб вона була схожа на першу фігуру.
Потім знайдіть сторону на другій фігурі, яка знаходиться в тому положенні, яке\(\overline{IJ}\) знаходиться на першій фігурі.
\(\overline{YZ}\)
Відповідь полягає в тому, що\(\overline{YZ}\) відповідає\(\overline{IJ}\). Марії потрібно розмістити двері своєї спальні посередині\(\overline{YZ}\) на репліці.
Приклад\(\PageIndex{2}\)
Наведені нижче цифри аналогічні. Яка сторона відповідає\(\overline{NO}\)?
 Малюнок\(\PageIndex{5}\)
Малюнок\(\PageIndex{5}\)Рішення
Спочатку розташуйте другу фігуру так, щоб вона виглядала як перша фігура.
Потім визначте сторону на другому малюнку, яка знаходиться в тому ж положенні,\(\overline{NO}\) що і на першому малюнку.
\(\overline{QR}\)
Відповідь полягає в тому, що\(\overline{QR}\) відповідає\(\overline{NO}\).
Приклад\(\PageIndex{3}\)
\(\overline{AB}\sim _____\)
Рішення
Спочатку подивіться, яка сторона другого трикутника відповідає заданому відрізку.
\(\overline{EF}\)
Потім завершіть проблему.
\(\overline{AB}\sim \overline{EF}\)
Відповідь така\(\overline{AB}\sim \overline{EF}\).
Приклад\(\PageIndex{4}\)
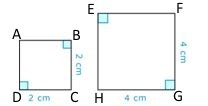
Що робить два квадрати схожими, якщо вони обидва мають чотири прямі кути?

Рішення
Спочатку перевірте, чи однакові довжини сторін.
Ні
Далі перевірте, чи однакова форма.
Так
Потім вкажіть, чому два квадрати схожі.
Однакова форма, різні розміри
Відповідь полягає в тому, що два квадрати схожі, оскільки вони мають однакову форму, але різні розміри.
Приклад\(\PageIndex{5}\)
У парі трикутників два трикутники схожі або конгруентні?
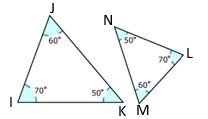 Малюнок\(\PageIndex{8}\)
Малюнок\(\PageIndex{8}\)Рішення
Спочатку перевірте, чи два трикутника однакового розміру.
Ні
Далі перевірте, чи є два трикутника однакової форми.
Так
Потім визначте, чи два трикутника схожі або конгруентні.
Схожі
Два трикутника схожі.
Рецензія
Використовуйте наступні цифри, щоб відповісти на кожне питання.

- Ці два трикутника схожі або конгруентні?
- Звідки ти знаєш?
- Яка сторона конгруентна\(\overline{AB}\)?
- Яка сторона конгруентна\(\overline{AC}\)?
- Яка сторона конгруентна\(\overline{RS}\)?
- Який кут конгруентний куту A?
- Який кут конгруентний куту B?
- Який кут конгруентний куту C?

- Дві фігури схожі або конгруентні?
- Чому?
- Яка сторона конгруентна\(\overline{NO}\)?
- Яка сторона конгруентна\(\overline{MN}\)?
- Яка сторона конгруентна\(\overline{ST}\)?
- Яка сторона конгруентна\(\overline{QT}\)?
- Яка сторона конгруентна\(\overline{OP}\)?
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 9.17.
Ресурси
Лексика
| Термін | Визначення |
|---|---|
| Конгруентний | Конгруентні фігури ідентичні за розміром, формою і мірою. |
| Кореспондент | Відповідні сторони між двома трикутниками - це сторони в одному відносному положенні. |
| Схожі | Дві фігури схожі, якщо вони мають однакову форму, але не обов'язково однакового розміру. |
Додаткові ресурси
Відео: Конгруентні та подібні трикутники
Практика: Відповідні частини аналогічних фігур