Skip to main content
LibreTexts - Ukrayinska

7.3: Подібні багатокутники та масштабні фактори

  1. Last updated
  2. Save as PDF
  • Page ID
    54661

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Подібні багатокутники

    Подібні багатокутники - це два багатокутника з однаковою формою, але не однакового розміру. Подібні багатокутники мають відповідні кути, які є конгруентними, і відповідні сторони, які пропорційні.

    F-D_4C684343ДД23Б5763АД 8777Б6Ф12ККА816961Б1Б1СС01793АФД0Е979БА+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Ці багатокутники не схожі:

    F-д_ЕФА 22797 АЕ949А277ЕЕ0С20Е 5551515326Б07Д822А67798060EA0AD4+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Масштабні фактори

    Подумайте про подібні багатокутники як про збільшення або зменшення тієї ж форми. Символ\ sim\) використовується для представлення подібності. Конкретні типи трикутників, чотирикутників та багатокутників завжди будуть однаковими. Наприклад, всі рівносторонні трикутники схожі і всі квадрати схожі . Якщо два полігони схожі, ми знаємо, що довжини відповідних сторін пропорційні. У подібних багатокутниках відношення однієї сторони багатокутника до відповідної сторони іншого називається масштабним коефіцієнтом. Співвідношення всіх частин багатокутника (включаючи периметри, діагоналі, медіани, середні сегменти, висоти) таке ж, як і співвідношення сторін.

    Що робити, якби вам сказали, що два п'ятикутника схожі, і вам дали довжини сторін кожного п'ятикутника. Як ви могли визначити масштабний коефіцієнт п'ятикутника #1 до п'ятикутника #2?

    Приклад\(\PageIndex{1}\)

    \(ABCD\)\(UVWX\)і нижче. Ці два прямокутника схожі?

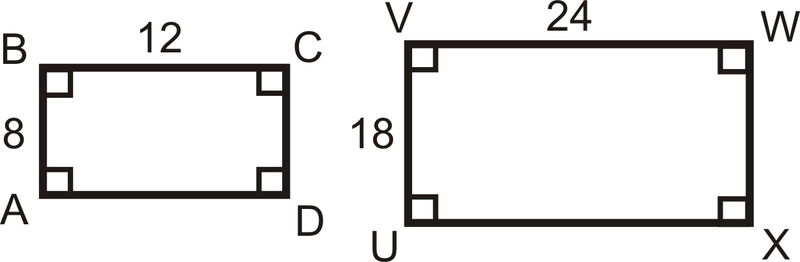
    F-D_CEB 4023630Б2 Ед 3А 3117308Б3Б3Б7255Б45 АФ А57879ФД1СА+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Всі відповідні кути є конгруентними, оскільки фігури є прямокутниками.

    Давайте подивимося, чи пропорційні сторони. \(\dfrac{8}{12}=\dfrac{2}{3}\)і\(\dfrac{18}{24}=\dfrac{3}{4}\). \(\dfrac{2}{3}\neq \dfrac{3}{4}\), Тому сторони не в однаковій пропорції, а прямокутники не схожі.

    Приклад\(\PageIndex{2}\)

    \(\Delta ABC\sim \Delta MNP\). Периметр\(\Delta ABC\) становить 150,\(AB=32\) а\(MN=48\). Знайдіть периметр\(\Delta MNP\).

    Рішення

    Від подібності висловлювання,\(AB\) і\(MN\) йдуть відповідні сторони. Коефіцієнт масштабування -\(\dfrac{32}{48}=\dfrac{2}{3}\) або\(\dfrac{3}{2}\). \ Delta ABC\) - це менший трикутник, тому периметр\(\Delta MNP\) дорівнює\(\dfrac{3}{2}(150)=225\).

    Приклад\(\PageIndex{3}\)

    Припустимо\(\Delta ABC\sim \Delta JKL\). Виходячи з твердження подібності, які кути є конгруентними, а які сторони пропорційні?

    Рішення

    Так само, як і в заяві конгруентності, конгруентні кути вибудовуються всередині заяви подібності. Отже,\(\angle A\cong \angle J\)\(\angle B\cong \angle K\), і\ кут C\ cong\ кут L\). Напишіть сторони в пропорції:\(\dfrac{AB}{JK}=\dfrac{BC}{KL}=\dfrac{AC}{JL}\). Зверніть увагу, що пропорція може бути записана по-різному. Наприклад, також\(\dfrac{AB}{BC}=\dfrac{JK}{KL}\) вірно.

    Приклад\(\PageIndex{4}\)

    \(MNPQ \sim RSTU\). Які значення мають\(x\),\(y\) і\(z\)?

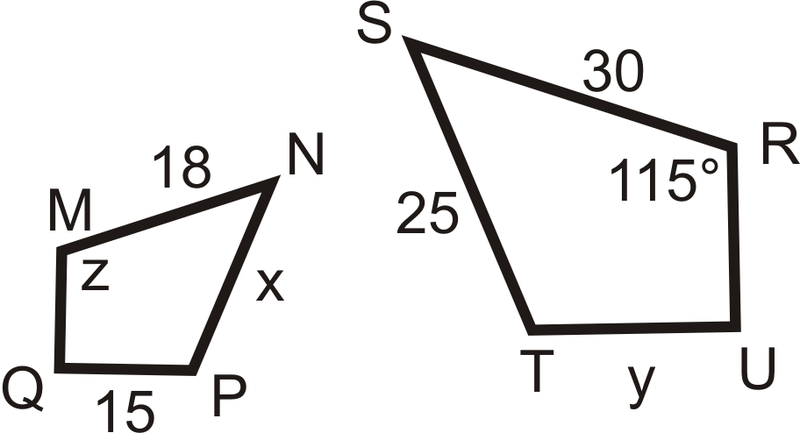
    Ф-д_617а 3Ф2Ф7Д46718561152566С9Б0КД66КС82Б3680471947Б+зображення_крихіткий+зображення_крихіткий_крошечкий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    У подібності твердження\(\angle M\cong \angle R\), так\(z=115^{\circ}\). Для\(x\) і\(y\), встановіть пропорції.

    \(\dfrac{18}{30}=\dfrac{x}{25} \qquad \dfrac{18}{30}=\dfrac{15}{y}\)

    \(450=30x \qquad 18y=450\)

    \(x=15\qquad y=25\)

    Приклад\(\PageIndex{5}\)

    \(ABCD\sim AMNP\). Знайдіть масштабний коефіцієнт і довжину\(BC\).

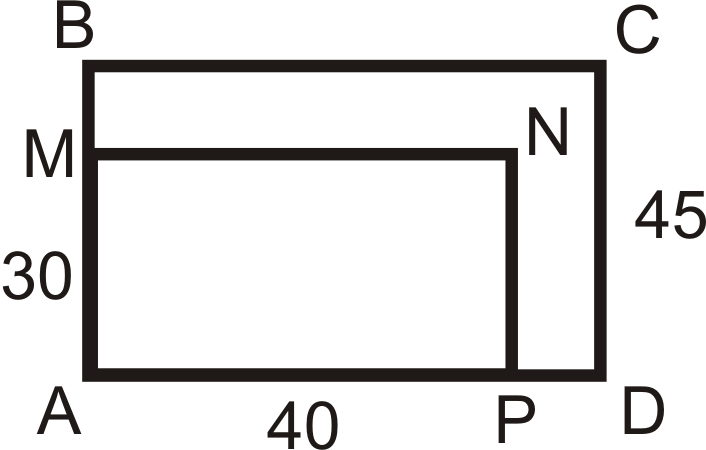
    F-д_ЕАФ 044Б3Д91С642Ф259308А77А955262А109Б3АФА4Б9Б9С0Ф935853С+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Вибудовуйте відповідні сторони,\(AB\) і\(AM=CD\), таким чином, коефіцієнт масштабу\(\dfrac{30}{45}=\dfrac{2}{3}\) або\(\dfrac{3}{2}\). Тому що\(BC\) знаходиться в великому прямокутнику, ми помножимо 40 на\(\dfrac{3}{2}\)\(\dfrac{3}{2}\) тому що більше 1. \(BC=\dfrac{3}{2}(40)=60\).

    Рецензія

    Для питань 1-8 визначте, чи є наступні твердження вірними чи хибними.

    1. Всі рівносторонні трикутники схожі.
    2. Всі рівнобедрені трикутники схожі.
    3. Всі прямокутники схожі.
    4. Всі ромби схожі.
    5. Всі квадрати схожі.
    6. Всі конгруентні багатокутники схожі.
    7. Всі подібні багатокутники є конгруентними.
    8. Всі звичайні п'ятикутники схожі.
    9. \(\Delta BIG \sim \Delta HAT\). Перерахуйте конгруентні кути і пропорції для сторін.
    10. Якщо\(BI=9\) і\(HA=15\), то знайдіть масштабний коефіцієнт.
    11. Якщо\(BG=21\), знайдіть\(HT\).
    12. Якщо\(AT=45\), знайдіть\(IG\).
    13. Знайдіть периметр\(\Delta BIG\) і\(\Delta HAT\). Яке співвідношення периметрів?
    14. Баскетбольний майданчик НБА - це прямокутник, який становить 94 футів на 50 футів. Баскетбольний майданчик середньої школи - це прямокутник, який становить 84 футів на 50 футів. Чи схожі два прямокутника?
    15. Телевізори HD мають сторони в співвідношенні 16:9. Телевізори без HD мають сторони в співвідношенні 4:3. Чи еквівалентні ці два співвідношення?

    Використовуйте картинку праворуч, щоб відповісти на питання 16-20.

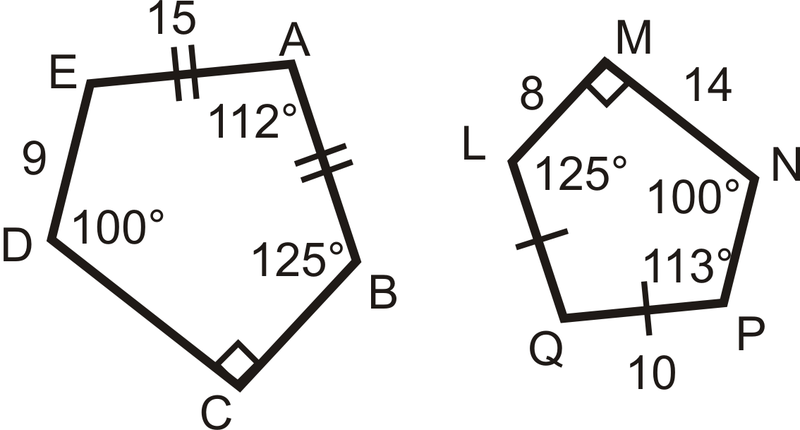
    F-д_FF937542A1CE934530E672CE08978600F9C2C81AFF28344BDE681F6+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)
    1. Знайти\(m\angle E\) і\(m\angle Q\).
    2. \(ABCDE\sim QLMNP\), знайти коефіцієнт масштабу.
    3. Знайти до н.е.
    4. Знайти компакт-диск.
    5. Знайти NP.

    Визначте, чи схожі наступні трикутники і чотирикутники. Якщо вони є, напишіть заяву подібності.

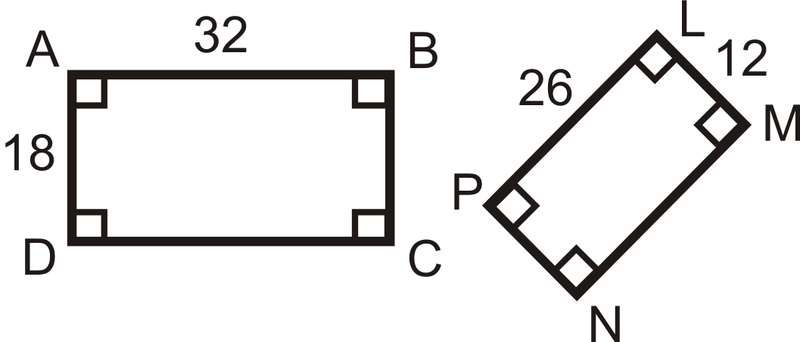
    1. F-D_3B2CF162АД 39С5А57481Б8556Б516 ЕЦБ7Д49 Даф 622441Ф4Б679468ДА+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
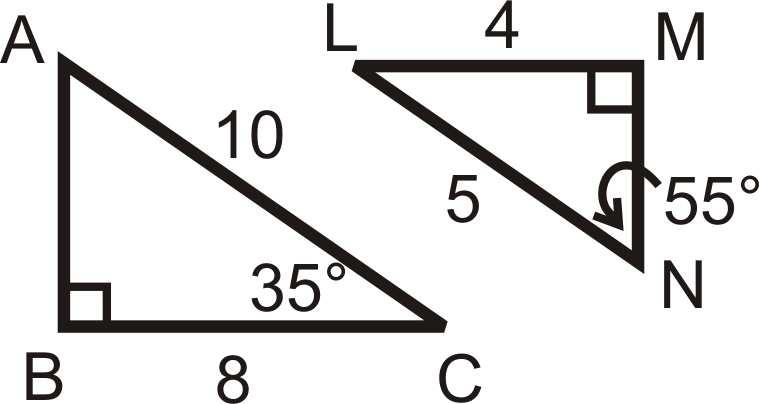
    2. Ф-Д_3ААА9435465 Ліжко 97859 А0883д 759Ф2 ДЕА ААА099885 АФ 17656E472B07+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
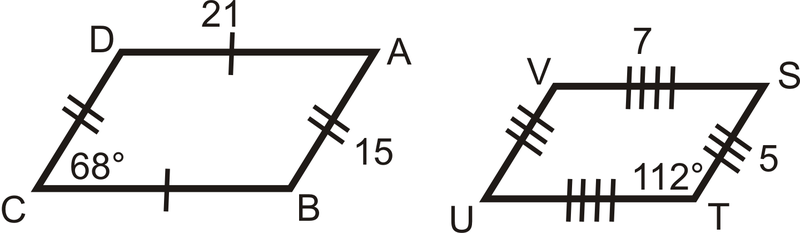
    3. F-д_5С9БФ 64162 АФД 9А60124 Кад567БФ 0Ф35Б654С198Ф98Б673312А4ЕЕ7+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
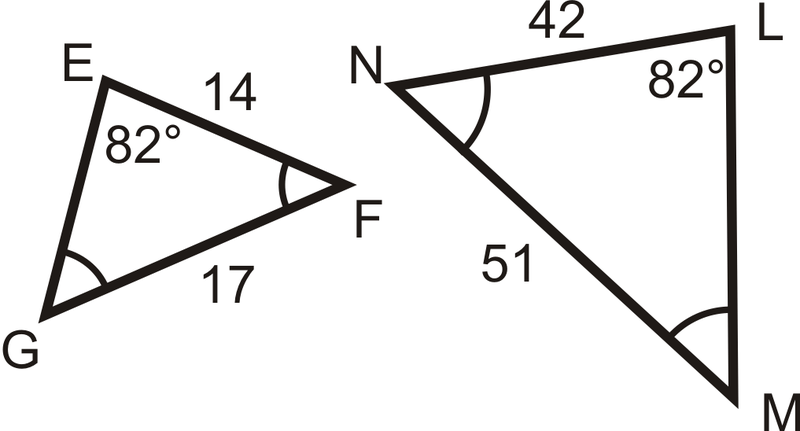
    4. F-D_022Ф90920А4 ББ717 БФ КД6 АД 2Б202615445Д05ФД0Д00Б7А8Ф489А508+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
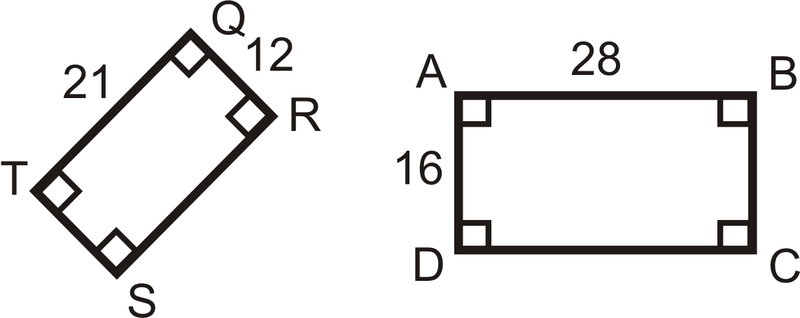
    5. F-D_9C8D53ФД037А513 ФД 8ДФ 37ЕЕ6Б3С209ФД6С1ADF7E63D13D925C76D+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
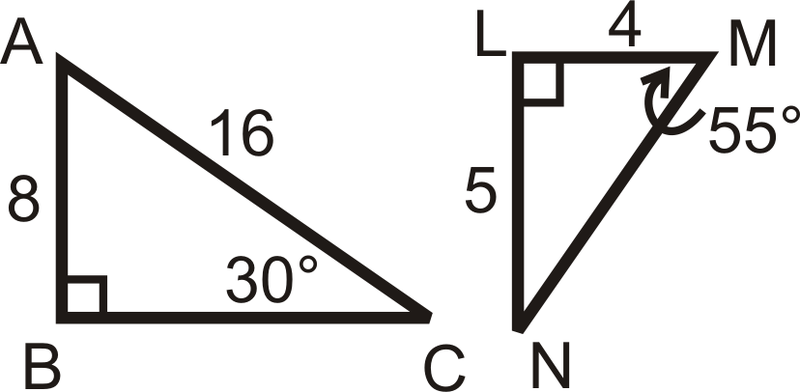
    6. Ф-д_Е0д0Ф5Б82208083С010827Б1С4ЕБ5С93С29А2852Д30Е0АЭ68502Ф27Ф+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
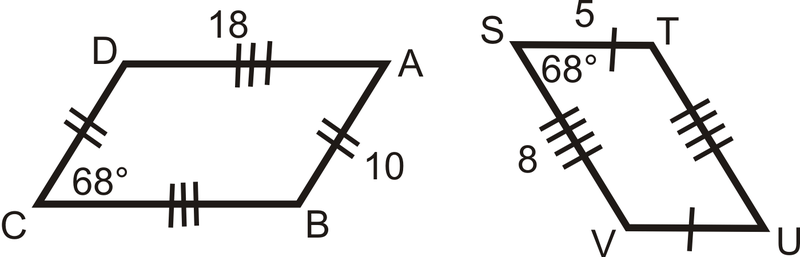
    7. F-D_9 Кабель CC05B23BDE23FFFFE4E60132d504F387168279B4C591C582AB8+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
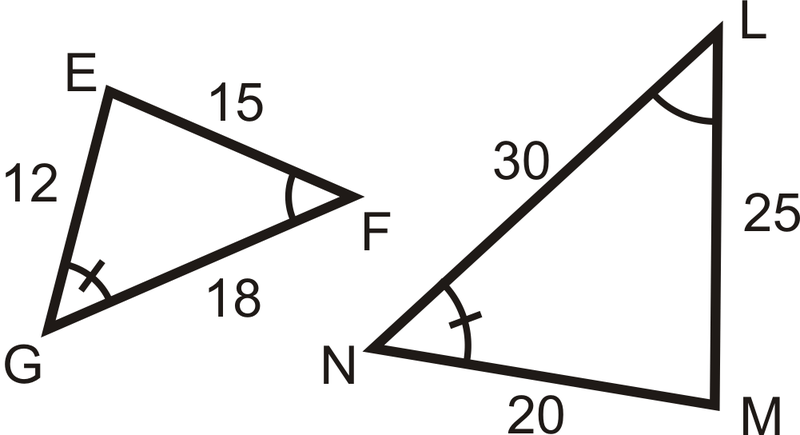    8. F-D_58A3 АБФ 245ДБ4Д4 АФ 55АЦ59Д1ДФ 91Д45ДФ Е8Б209Ф6Е884720DA84+зображення_крихіткий+зображення_крихіткий.PNG\(\Індекс сторінки малюнка {14}\)
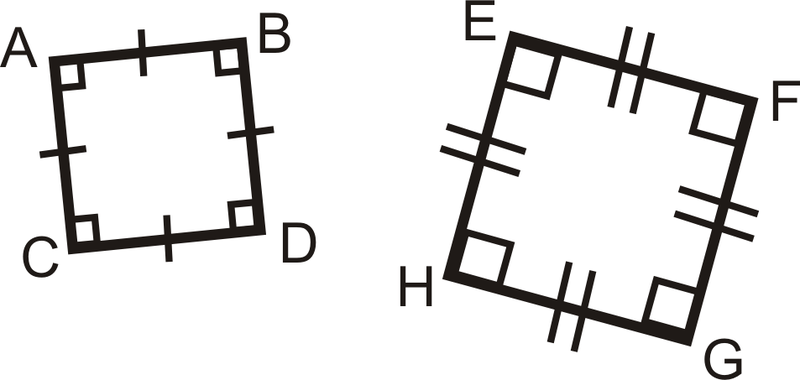
    9. F-D5434856E7A8ЕЕЕ345 ЕАЕ1 АААФ 050Ф65Е57Д0559 ББ8328Ф566212+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
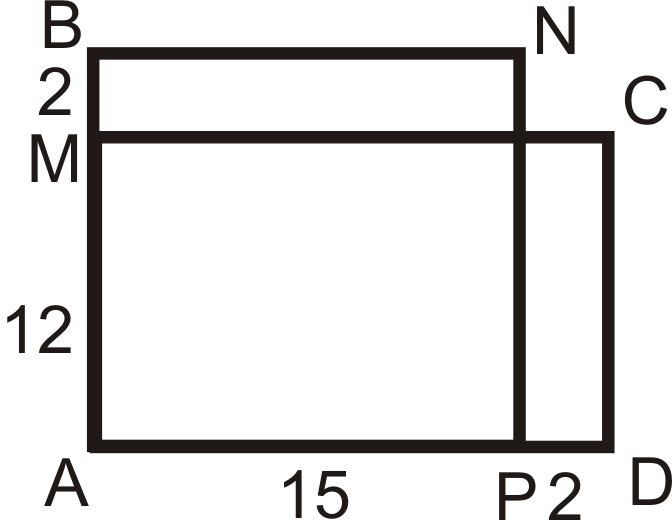
    10. F-D_07B362 ФАБ 618Е 3ЕЕ59КФ4А85ФБ9Е2С077718 ЕА815019Д17Б487ЕБ+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)

    Ресурси

    Лексика

    Термін Визначення
    подібні багатокутники Два багатокутника з однаковою формою, але не однакового розміру. Відповідні кути подібних багатокутників конгруентні (точно такі ж) і відповідні сторони пропорційні (в однаковому співвідношенні). У подібних багатокутниках відношення однієї сторони багатокутника до відповідної сторони іншого називається масштабним коефіцієнтом.
    Конгруентний Конгруентні фігури ідентичні за розміром, формою і мірою.
    Пропорція Пропорція - це рівняння, яке показує два еквівалентних співвідношення.
    Коефіцієнт масштабування Масштабний коефіцієнт - це відношення масштабу до вихідного або фактичного виміру, написаного в найпростішій формі.
    синус Синус кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, протилежної заданому куту, на довжину гіпотенузи.
    Тригонометричні коефіцієнти Співвідношення, які допомагають нам зрозуміти відносини між сторонами і кутами прямих трикутників.