7.2: Співвідношення та пропорції в аналогічних цифрах

Last updated
Save as PDF

Page ID: 54709

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Спростіть способи порівняння двох чисел.

Пропорції

Пропорція - це два співвідношення, які встановлюються рівними один одному. Зазвичай співвідношення в пропорціях пишуть у вигляді дробів. Прикладом пропорції є$\dfrac{2}{x}=510$. Щоб вирішити пропорцію, потрібно перехресне множення. Теорема про перехресне множення, яка дозволяє вирішувати пропорції за допомогою цього методу, стверджує, що if$a$$b$,$c$,, і$d$ є дійсними числами, з$b\neq 0$$d\neq 0$ і і якщо$\dfrac{a}{b}=\dfrac{c}{d}$, то$\dfrac{a}{d}=\dfrac{b}{c}$. Перехресне множення дозволяє позбутися від дробів у нашому рівнянні. Теорема про перехресне множення має кілька підтеорем, званих слідством.

Наслідок #1: Якщо$a$,$b$,$c$, і$d$ ненульові і$\dfrac{a}{b}=\dfrac{c}{d}$, то$\dfrac{a}{c}=\dfrac{b}{d}$.

Перемикач$b$ і$c$ .

Наслідок #2: Якщо$a$,$b$,$c$, і$d$ ненульові і$\dfrac{a}{b}=\dfrac{c}{d}$, то$\dfrac{d}{b}=\dfrac{c}{a}$.

Перемикач$a$ і$d$.

Наслідок #3: Якщо$a$,$b$$c$, і$d$ є ненульовими і$\dfrac{a}{b}=\dfrac{c}{d}$\), то$\dfrac{b}{a}=\dfrac{c}{d}$.

Переверніть кожне співвідношення догори дном.

Слідство #4: Якщо$a$,$b$$c$, і$d$ є ненульовими і\ dfrac {a} {b} =\ dfrac {c} {d}\), то$\dfrac{a+b}{b}=\dfrac{c+d}{d}$.

Наслідок #5: Якщо$a$,$b$,$c$, і$d$ ненульові і$\dfrac{a}{b}=\dfrac{c}{d}$, то$\dfrac{a−b}{b}=\dfrac{c−d}{d}$.

Що робити, якщо вам сказали, що масштабна модель пітона знаходиться в співвідношенні 1:24? Якщо модель вимірює довжину 0, 75 футів, як довго справжній пітон?

Приклад$\PageIndex{1}$

На малюнку,$\dfrac{AB}{XY}=\dfrac{BC}{YZ}=\dfrac{AC}{XZ}$.

Знайдіть заходи$AC$ і$XY$.

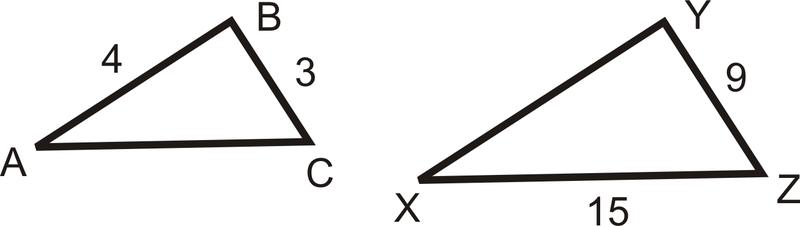
F-D_59AC68 Додати 548127 ДФФ 1Е85А57Д05СА413АА64908659А98 АААА229А9Е+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок$\PageIndex{1}$

Рішення

Підключіть довжини сторін, які ми знаємо.

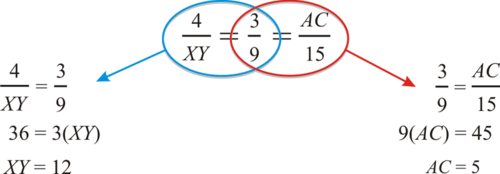
Приклад$\PageIndex{2}$

На малюнку,$\dfrac{AB}{BE}=\dfrac{AC}{CD}$. Знайти$BE$.

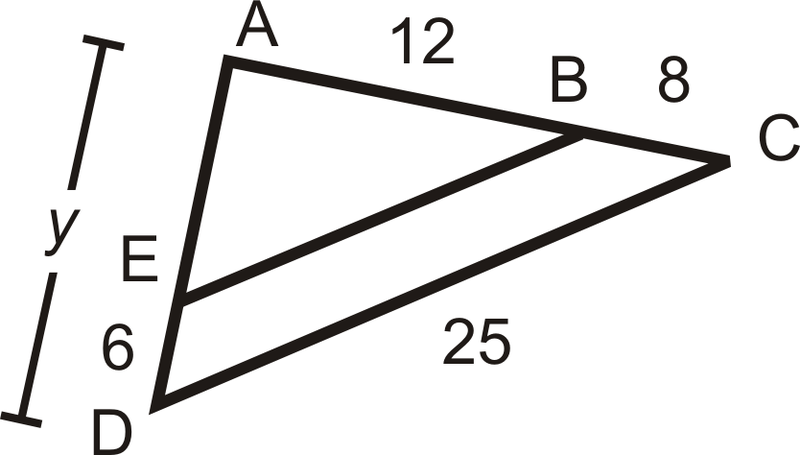
F-D_45 ЕФ6 ЕФ74834Д8 СА70 КД2А370Е28 ДФФ 281С051575892 ЕКА А35378+зображення_крихіткий+зображення_крихіткий_png — Малюнок$\PageIndex{3}$

Рішення

Підставляємо в довжину відомих нам сторін.

$\begin{aligned} \dfrac{12}{BE}=\dfrac{20}{25} \rightarrow 20(BE)&=12(25)\\ BE&=15\end{aligned}$

Приклад$\PageIndex{3}$

Вирішіть пропорції. Пам'ятайте, щоб вирішити пропорцію, потрібно перехресне множення.

$\dfrac{4}{5}=\dfrac{x}{30}$
$\dfrac{y+1}{8}=\dfrac{5}{20}$
$\dfrac{6}{5}=\dfrac{2x+4}{x−2}$

Рішення

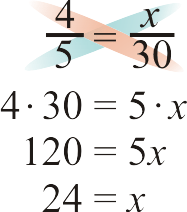
Малюнок$\PageIndex{4}$
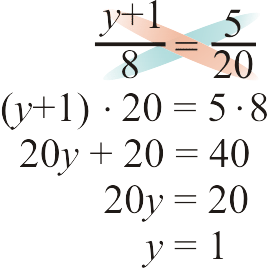
Малюнок$\PageIndex{5}$
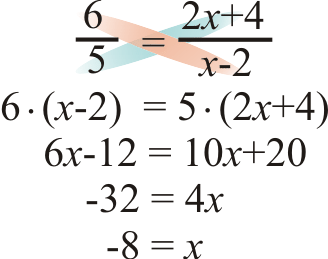
Малюнок$\PageIndex{6}$

Приклад$\PageIndex{4}$

Ваші батьки мають креслення архітектора свого будинку. На папері розміри будинку становлять 36 в на 30 дюймів. Якщо коротша довжина будинку насправді 50 футів, яка довша довжина?

Рішення

Щоб вирішити, спочатку налаштуйте пропорцію. Якщо коротша довжина становить 50 футів, то вона вирівнюється з 30 дюймів, тим коротша довжина паперу розмірів.

$\begin{aligned}\dfrac{30}{3}6=\dfrac{50}{x} \rightarrow 30x&=1800 \\ x&=60 \qquad \text{The longer length is 60 feet.}\end{aligned}$

Приклад$\PageIndex{5}$

Припустимо, у нас є пропорція$\dfrac{2}{5}=\dfrac{14}{35}$. Напишіть три справжні пропорції, які слідують.

Рішення

Перш за все, ми знаємо, що це справжня пропорція, тому що ви б$\dfrac{2}{5}$ помножили на$\dfrac{7}{7}$, щоб отримати$\dfrac{14}{35}$. Використовуючи перші три слідства:

$\dfrac{2}{14}=\dfrac{5}{35}$
$\dfrac{35}{5}=\dfrac{14}{2}$
$\dfrac{5}{2}=\dfrac{35}{14}$

Рецензія

Вирішіть кожну пропорцію.

$\dfrac{x}{10}=\dfrac{42}{35}$
$\dfrac{x}{x−2}=\dfrac{5}{7}$
$\dfrac{6}{9}=\dfrac{y}{24}$
$\dfrac{x}{9}=\dfrac{16}{x}$
$\dfrac{y−3}{8}=\dfrac{y+6}{5}$
$\dfrac{20}{z+5}=\dfrac{16}{7}$
Шона проїхала 245 миль і використовувала 8.2 галонів газу. При такій же швидкості, якщо вона проїхала 416 миль, скільки галонів газу їй знадобиться? Округлити до найближчої десятої.
Президент, віце-президент та фінансовий директор компанії поділяють прибуток у співвідношенні 4:3: 2. Якщо компанія зробила $1,800,000 минулого року, скільки отримала кожна людина?

Враховуючи істинну пропорцію$d$,$\dfrac{10}{6}=\dfrac{15}{d}=\dfrac{x}{y}$ і$x$, і$y$ є ненульовими, визначте, чи відповідають і такі пропорції.

$\dfrac{10}{y}=\dfrac{x}{6}$
$\dfrac{15}{10}=\dfrac{d}{6}$
$\dfrac{6+10}{10}=\dfrac{y+x}{x}$
$\dfrac{15}{x}=\dfrac{y}{d}$

З питань 13-16,$\dfrac{AE}{ED}=\dfrac{BC}{CD}$ і$\dfrac{ED}{AD}=\dfrac{CD}{DB}=\dfrac{EC}{AB}$.

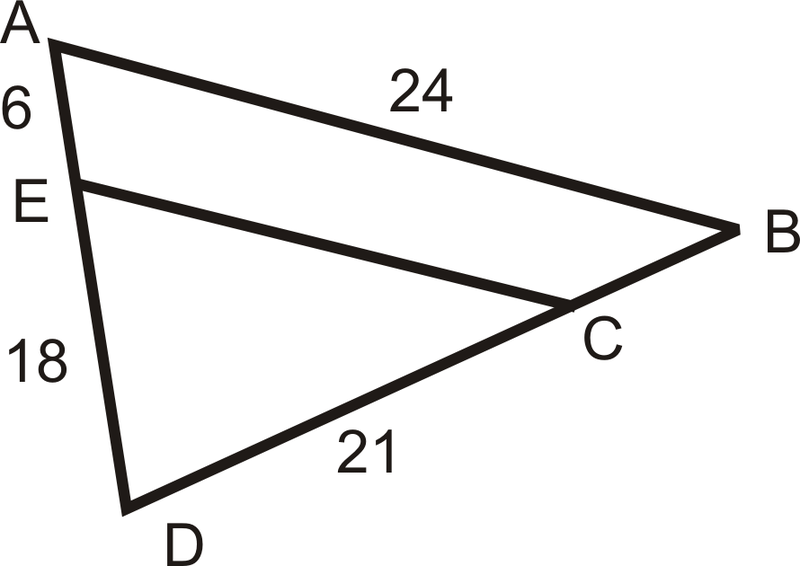
F-D_443 ЕАД 3096Е684БКФ 91Е7531 С10ЕД 626 СА50Ф63Б885624 ББ24ААА03+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок$\PageIndex{7}$

Знайти БД.
Знайти ЕК.
Знайти CB.
Знайти AD.

Ресурси

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 7.2.

Лексика

Термін	Визначення
наслідок	Теорема, яка випливає безпосередньо з іншої теореми.
пропорція	Два співвідношення, які встановлюються рівними один одному.
співвідношення	Спосіб порівняння двох чисел. Співвідношення можна записати трьома способами:\ dfrac {a} {b}, a:b і a до b.
Крос-продукти	Щоб спростити пропорцію за допомогою перехресних виробів, помножте діагоналі кожного співвідношення.
Теорема про перехресне множення	Теорема про перехресне множення стверджує$a$, що якщо$b$,$c$ і$d$ є дійсними числами, з$b\neq 0$$d\neq 0$ і і якщо$\dfrac{a}{b}=\dfrac{c}{d}$, то$\dfrac{a}{d}=\dfrac{b}{c}$.

Додаткові ресурси

Інтерактивний елемент

Відео: Співвідношення

Види діяльності: Форми коефіцієнтів Дискусійні питання

Навчальні посібники: Співвідношення та пропорції навчальний посібник

Практика: Співвідношення і пропорції в аналогічних цифрах

Реальний світ: У ляльковому будинку