Skip to main content
LibreTexts - Ukrayinska

6.20: Теорема про дотичну секантну

  1. Last updated
  2. Save as PDF
  • Page ID
    54454

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Добуток зовнішнього відрізка і цілого секанса дорівнює квадрату дотичної до тієї ж точки.

    Відрізки від секансів і дотичних

    Якщо дотична і січна зустрічаються в загальній точці поза колом, створені сегменти мають аналогічне відношення до двох січних променів.

    Теорема дотичної секантного сегмента: Якщо дотична і січна витягуються із загальної точки поза колом (а сегменти позначені як на малюнку нижче), то\(a^2=b(b+c)\).

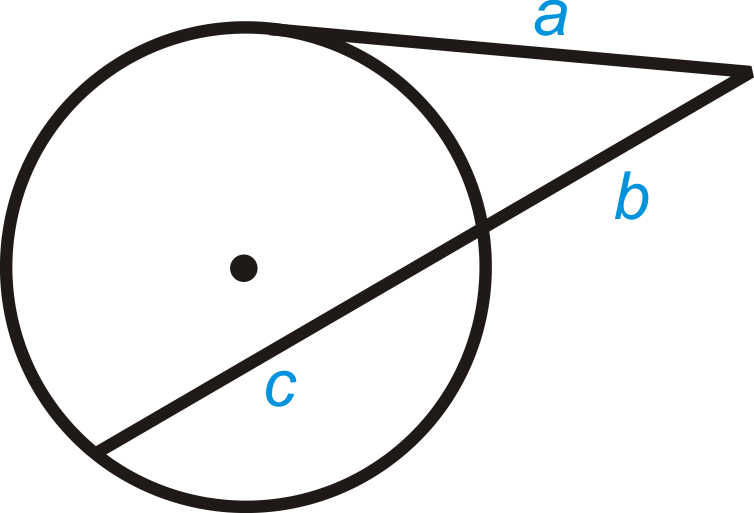
    Ф-Д_КДА 77Ф0Ф455 ЕД додати 01497F019B2B39C5E95AE1CF9fd36164785439+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Що робити, якщо вам дали коло з дотичною і січною, які перетинаються за межами кола? Як можна використовувати довжину деяких відрізків, утворених їх перетином, для визначення довжин невідомих відрізків?

    Приклад\(\PageIndex{1}\)

    Знайти\(x\). Спрощуйте будь-які радикали.

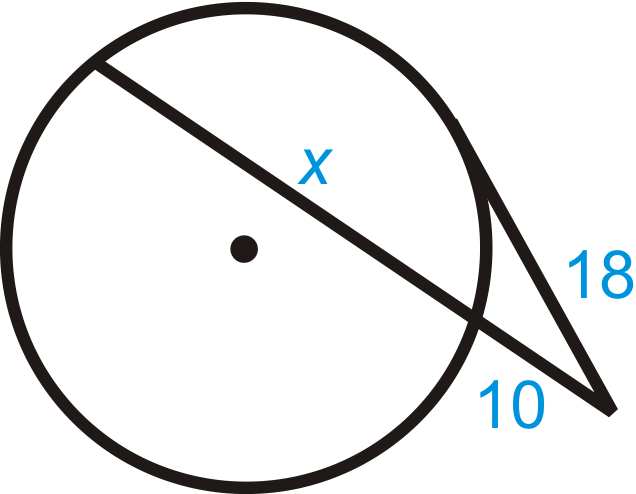
    F-D_13A0E460AD2FE519 ЕЦ1А021С6 ФК8 А2ДФ 3Ф8А5ЕБ1Б9682 Фад08ЕБЕ84+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Скористайтеся теоремою дотичної секантного відрізка.

    \(\begin{aligned} 18^2&=10(10+x) \\ 324&=100+10x \\ 224&=10x \\ x&=22.4\end{aligned}\)

    Приклад\(\PageIndex{2}\)

    Знайти\(x\). Спрощуйте будь-які радикали.

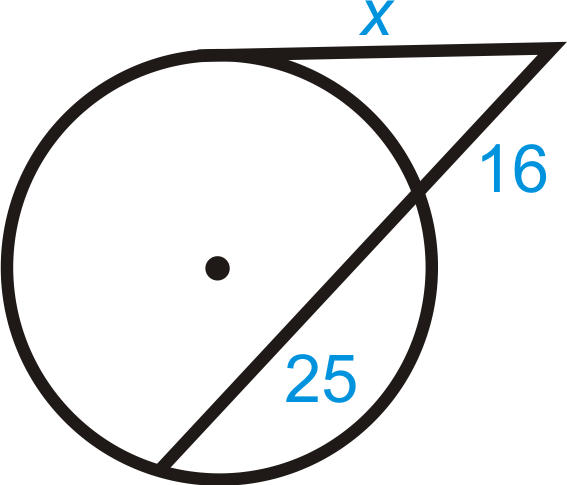
    F-D_0AE0 ЕЦВЕ 660D16 БББ4 БББ8 ЕДД 3С5 CFB652D8E 7607586C46A8BA3+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Скористайтеся теоремою дотичної секантного відрізка.

    \(\begin{aligned} x^2&=16(16+25) \\ x^2&=656 \\ x&=4\sqrt{41}\end{aligned}\)

    Приклад\(\PageIndex{3}\)

    Знайти довжину відсутнього відрізка.

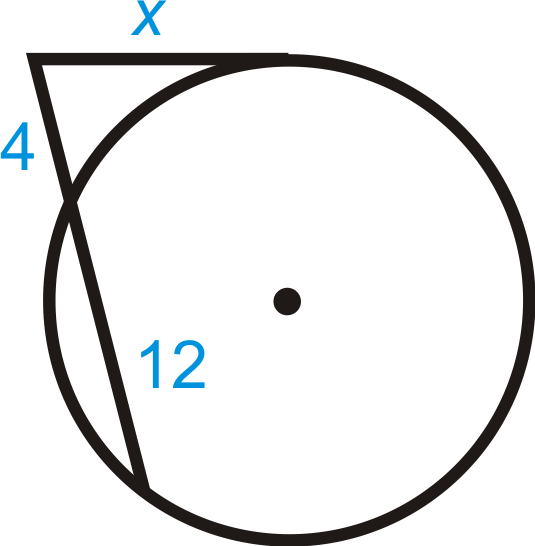
    F-д_6ф6д8c867a669E69F1F2A ADC 71 Деб091Ед 3БК 974039E7D292C9+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Скористайтеся теоремою дотичної секантного відрізка.

    \(\begin{aligned} x^2&=4(4+12) \\ x^2&=4\cdot 16=64 \\ x&=8\end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Заповніть бланк, а потім вирішіть для відсутнього сегмента.

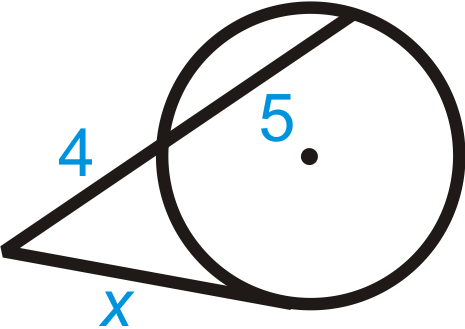
    F-д_ФБФ Б 192Б288Е2ЕФ96697А491914793398Ф4С77Б4А4А4С0192E07EC917+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    \(\text{______}=\text{______}(4+5)\)

    \(\begin{aligned} x^2&=4(4+5) \\ x^2&=36 \\ x&=6\end{aligned}\)

    Приклад\(\PageIndex{5}\)

    Знайти значення відсутнього відрізка.

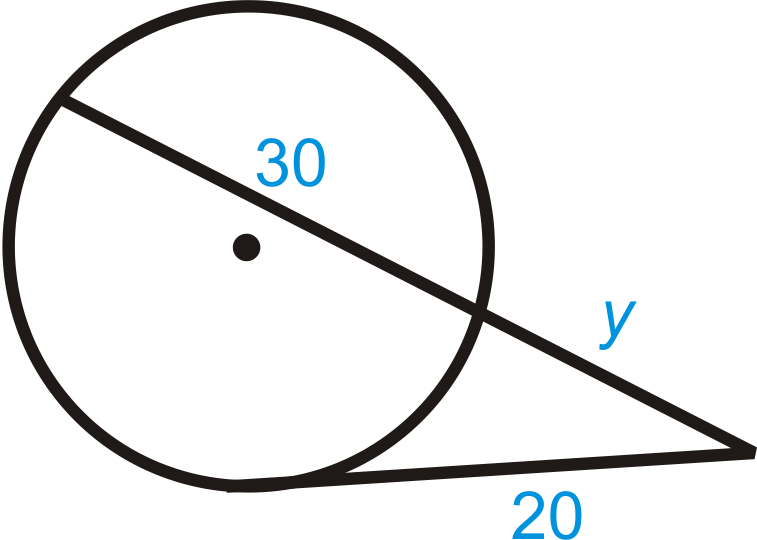
    F-д_91f8c15f53238269ad4 ББФ Ф 56E089CA36e449cd099cd099a7729227348E7+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Скористайтеся теоремою дотичної секантного відрізка.

    \(\begin{aligned} 20^2&=y(y+30) \\ 400&=y^2+30y \\ 0&=y^2+30y−400 \\ 0&=(y+40)(y−10) \\ y&=\xcancel{−40},10 \end{aligned}\)

    Рецензія

    Заповніть пропуски для кожної задачі нижче, а потім вирішіть для відсутнього відрізка.

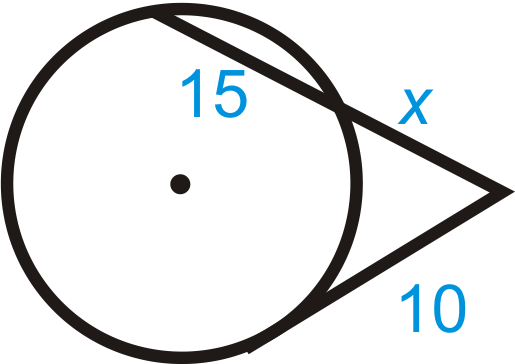
    1. F-D_7D0247335ЕФ 3Ф Ф 4А9616БД79ФКД 309484Е5Д9С4ФК5Б93ДБ222А70Д+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)

    \(10^2=x(\text{______}+\text{______})\)

    Знайдіть\(x\) на кожній схемі нижче. Спрощуйте будь-які радикали.

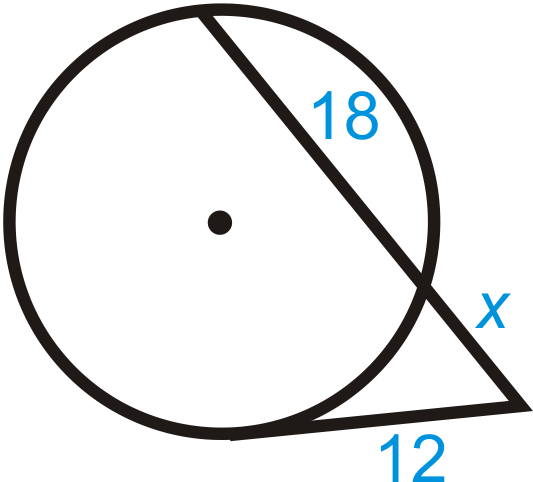
    1. F-д_Д68Ф3С9Б01Д90ФКА84Д1Е74Д35ФБФ 2АА330Д2383СЕ9651Б419А7ФД58+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
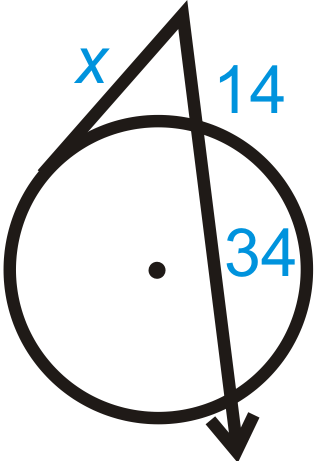
    2. F-д_д62БД ДФ 1Б8С22803Д84А153Е088ФБК 3ФДА75А1А 83146507037Д5АА+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
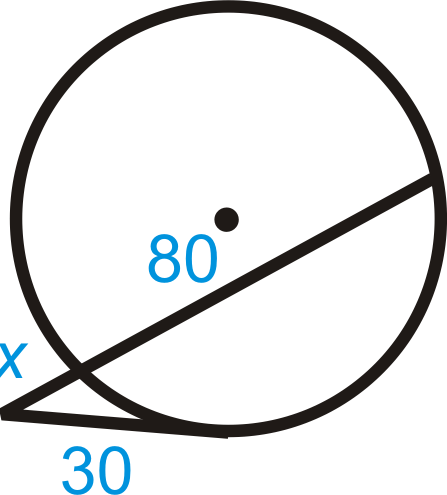
    3. F-D_F9ФД26ФД9 CFD49C5A2044А317c72993ФДБ6ДЕ2ФД45C58AB52D0371+зображення_крихіткий+зображення_крихітковий_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
    4. Опишіть і виправте помилку при знаходженні\(y\).
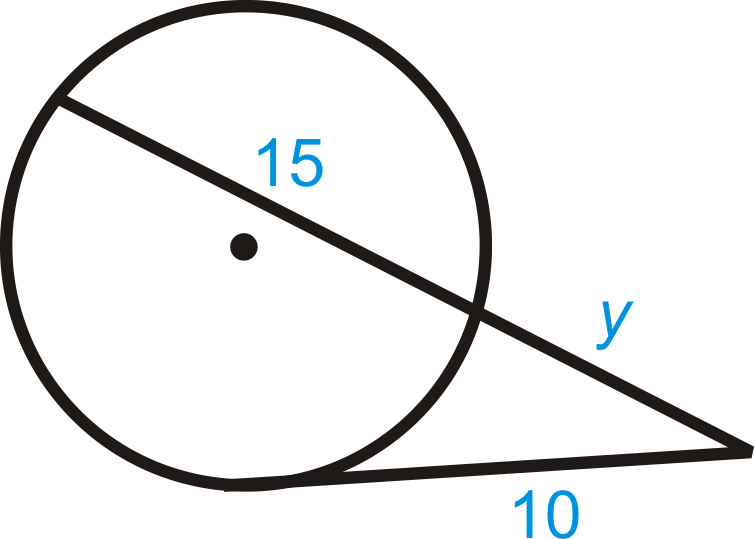
      F-д_ББ1С9 CEAED 94Б7С9Д7557А39345 ДБ5 БАЕ47Б84Б2208ФФАД 1105+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)

    \(\begin{aligned} 10\cdot 10&=y\cdot 15y \\ 100&=15y^2 \\ \dfrac{20}{3}&=y^2 \\ \dfrac{2\sqrt{15}}{3}&=y \color{red} \leftarrow \text{y is \underline{not} correct}\end{aligned}\)

    Вирішити для невідомої змінної.

    1. F-D_FE7 ЕД ЕДС6 БЕ43250Д4 СА6Д 7А 78740Б3 ЕДД7Б34А6 А834847Ф5Д725+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
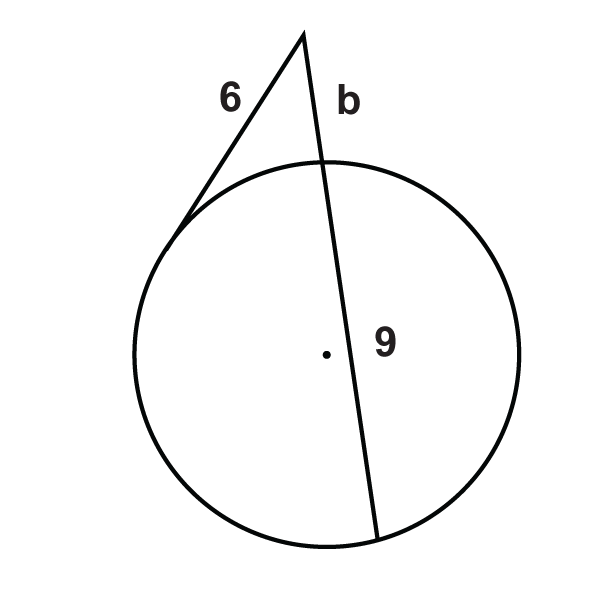
    2. Ф-д_76д7Б110773АФ 85А0А2Ф58Б1786Ф6050ДА557641 ББ01143039 КБС294+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
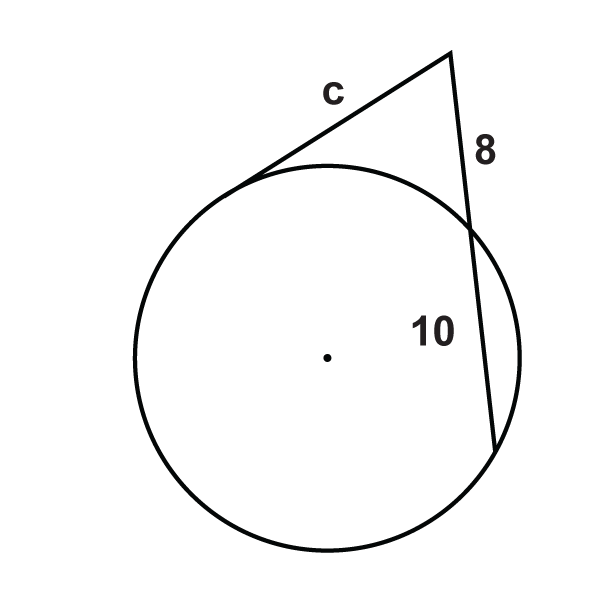
    3. F-D_2B914FFF7E2B43 Кабін 50Ф8 Дед С651828d426d702DA13895C5FD47AEB3+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
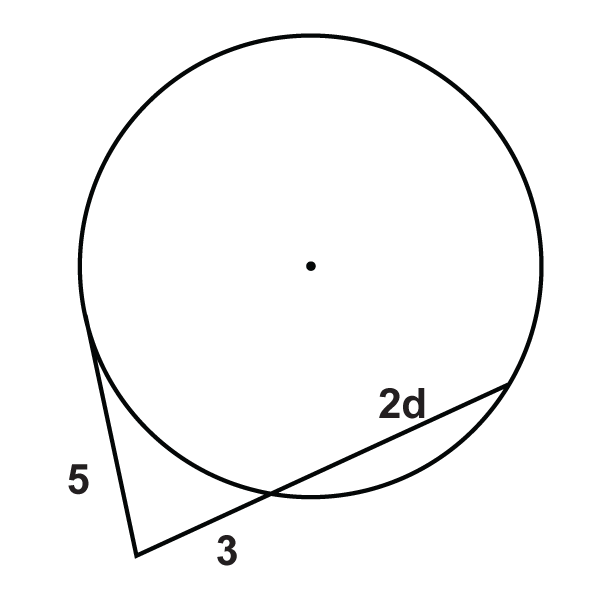
    4. F-DB249129 ФФ Ф 187Б84255Б9С53 Дед 2С7Б17ДК469DA64498E8C1BB8FF7+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
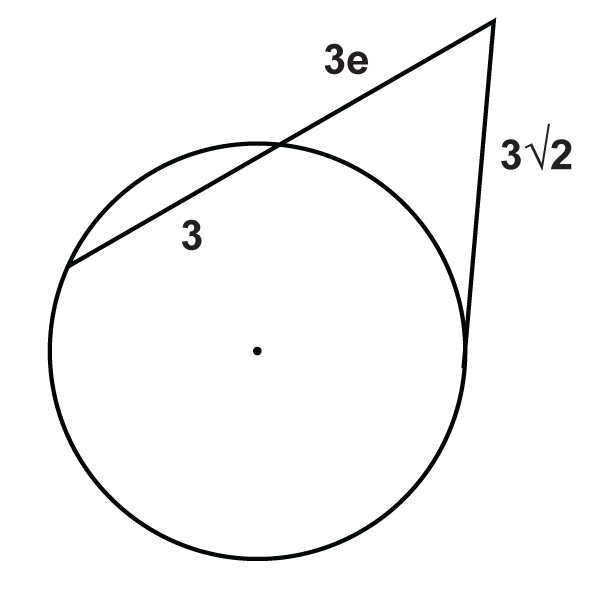
    5. F-D_375Ф471667590Б8 КБД Баф 219108БК 12Ф28295Б671 АФ CF959D9E96+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
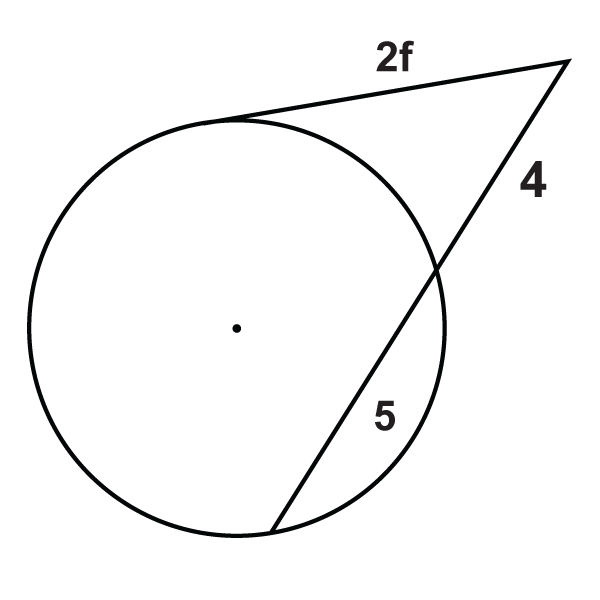
    6. F-D_960244500Б47Ф35С3Д5ДФ 2 ЕАФ 70Е8Б1Б5А7083СА82ДФА68AAE2A287+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)
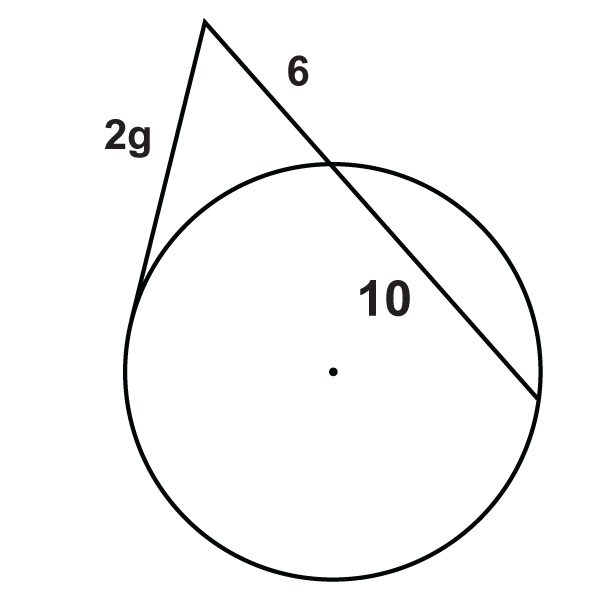
    7. F-Д_5Д05980ФД6182699E3Б03Д5Е3185ФКФ3С2А7А408135С7Б1С019+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)
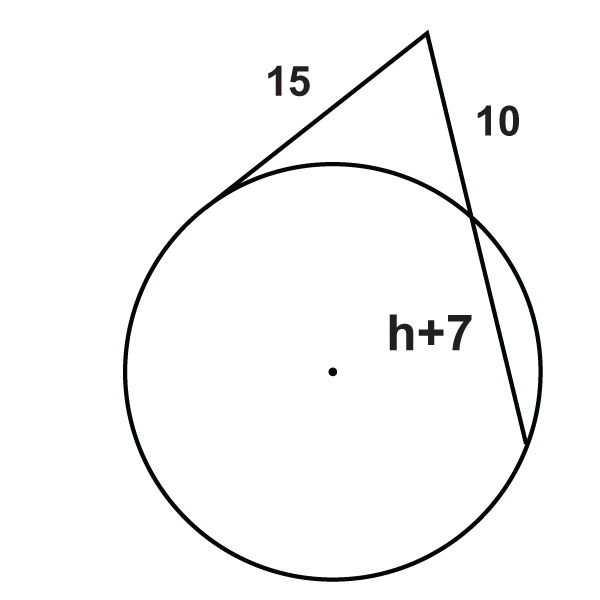
    8. F-д_ЕАЕ 693Ф59ФБ 80Ф10ДЕ47С6ЕФ 59Ф4 Каб 787ДБ044034 АЕЕ1443+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)
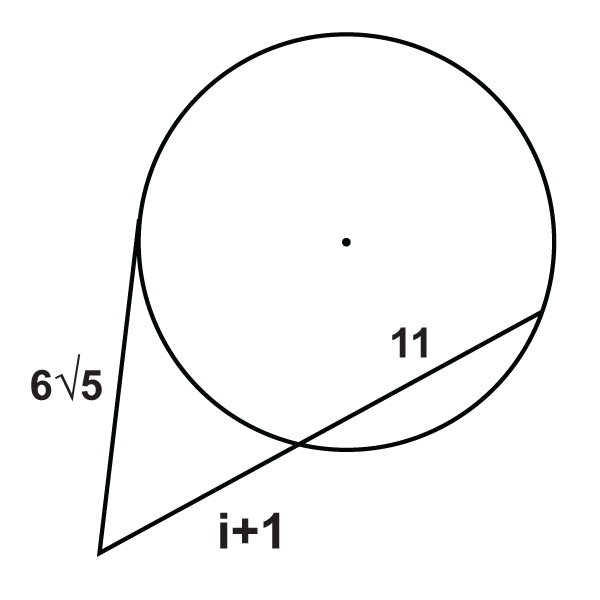
    9. Ф-д_Е50С214А72 А66Б8Ф5Е91Д8БА4 БДБ0ФА2Ф007ФБФ 13270Ф0980424E2+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{20}\)
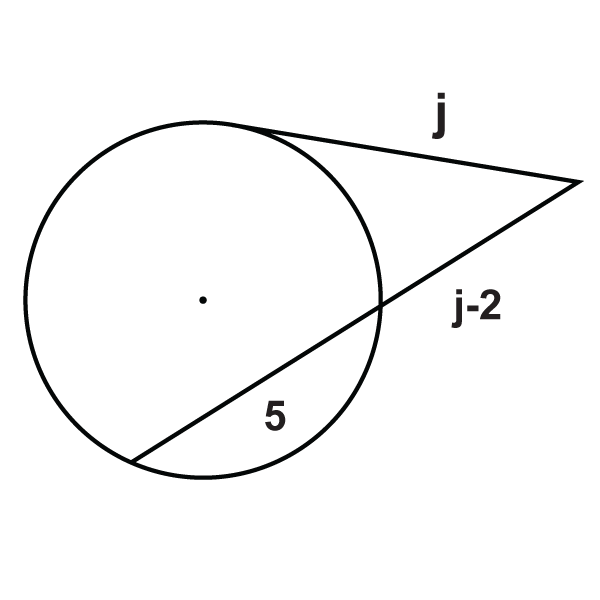
    10. Ф-Д_КА 936С2Ф57А6140Е 5А2БДБ5ФК 21601553ДЕ4 CFBEBA650592CA3 ЕБК+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{21}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 9.11.

    Лексика

    Термін Визначення
    центральний кут Кут, утворений двома радіусами і вершина якого знаходиться в центрі кола.
    акорд Відрізок лінії, кінцеві точки якого знаходяться на колі.
    коло Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    вписаний кут Кут з його вершиною на колі і сторони якого є хордами.
    перехоплена дуга Дуга, яка знаходиться всередині вписаного кута і кінцеві точки якої знаходяться на куті.
    точка дотику Точка, де дотична лінія стосується кола.
    радіус Відстань від центру до зовнішнього обідка кола.
    Секантний Секанс кута в прямокутному трикутнику - це величина, знайдена діленням довжини гіпотенузи на довжину сторони, прилеглої до заданого кута. Відношення секанс - це зворотне косинусного відношення.
    Теорема про дотичні січні відрізки Якщо дотична і січна намальовані із загальної точки за межами кола (а відрізки позначені як на малюнку нижче), то\(a^2 = b(b+c)\).

    Додаткові ресурси

    Інтерактивний елемент

    Діяльність: Сегменти з секансів і дотичних Питання обговорення

    Навчальні посібники: Кола: Сегменти та довжини навчальний посібник

    Практика: Теорема про дотичну секантну