6.16: Кути на колі та всередині

Кути, вершини яких знаходяться на окружності кола або утворені дотичними лініями і хордами.

Коли ми говоримо, що кут знаходиться на колі, ми маємо на увазі вершина знаходиться на краю кола. Одним з типів кута на колі є вписаний кут (див. Вписані кути в колах). Інший тип кута на колі - це той, утворений дотичною і хордою.

Теорема хорда/дотичного кута: Міра кута, утвореного хордою та тангенсом, що перетинаються на колі, є половиною міри перехопленої дуги.

Малюнок$\PageIndex{1}$

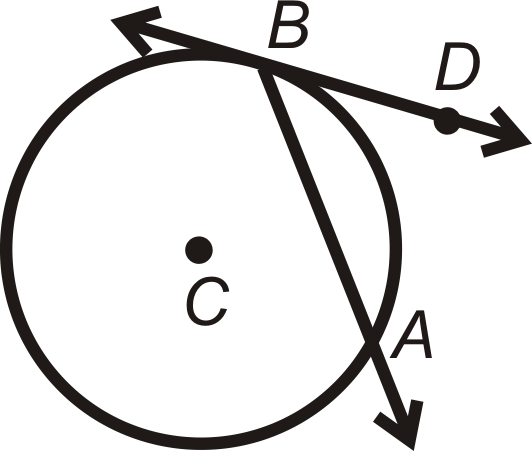
$m\angle DBA=\dfrac{1}{2}m\widehat{AB}$

Якщо два кути, з їх вершинами на колі, перехоплюють одну і ту ж дугу, то кути конгруентні.

Кут знаходиться всередині кола, коли вершина лежить де-небудь всередині кола.

Теорема кута перетину хорд: Міра кута, утвореного двома хордами, які перетинаються всередині кола, є середнім показником мір перехоплених дуг.

Малюнок$\PageIndex{2}$

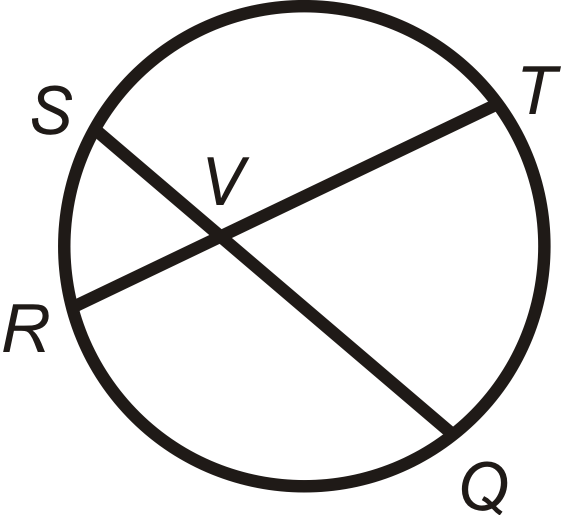
$\begin{aligned}m\angle SVR&=\dfrac{1}{2}(m\widehat{SR} +m\widehat{TQ} )=m\widehat{SR} +m\widehat{TQ} 2=m\angle TVQ \\ m\angle SVT&=\dfrac{1}{2}(m\widehat{ST} +m\widehat{RQ} )=m\widehat{ST} +m\widehat{RQ} 2=m\angle RVQ\end{aligned}$

Що робити, якщо вам дали коло або з акордом і дотичною, або двома акордами, які зустрічаються в загальній точці? Як ви могли б використовувати міру дуги (ів), утворених цими частинами кола, щоб знайти міру кутів, які вони роблять на або всередині кола?

Приклад$\PageIndex{1}$

Знайти$x$.

Малюнок$\PageIndex{3}$

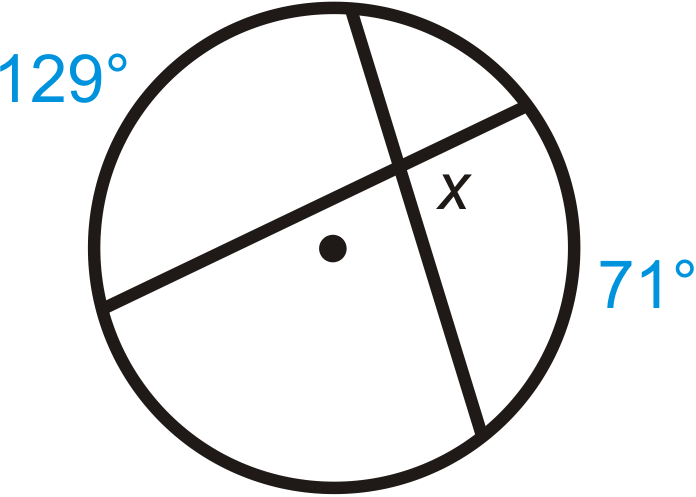
Рішення

Скористайтеся теоремою кута перетину хорд, щоб написати рівняння.

$x=\dfrac{129^{\circ}+71^{\circ}}{2}=\dfrac{200^{\circ}}{2}=100^{\circ}$

Приклад$\PageIndex{2}$

Знайти$x$.

Малюнок$\PageIndex{4}$

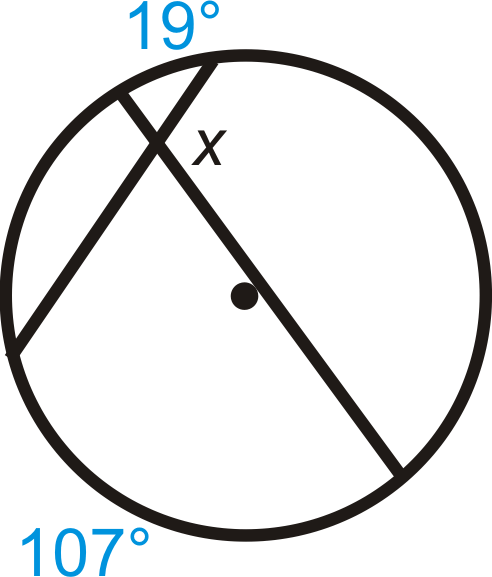
Рішення

Скористайтеся теоремою кута перетину хорд, щоб написати рівняння.

$x$є додатковим до кута, який є середнім показником заданих перехоплених дуг. Ми називаємо цей додатковий кут$y$.

$y=\dfrac{19^{\circ}+107^{\circ}}{2}=\dfrac{126^{\circ}}{2}=63^{\circ} \qquad x+63^{\circ}=180^{\circ}; \: x=117^{\circ}$

Приклад$\PageIndex{3}$

Знайти$m\angle BAD$.

Малюнок$\PageIndex{5}$

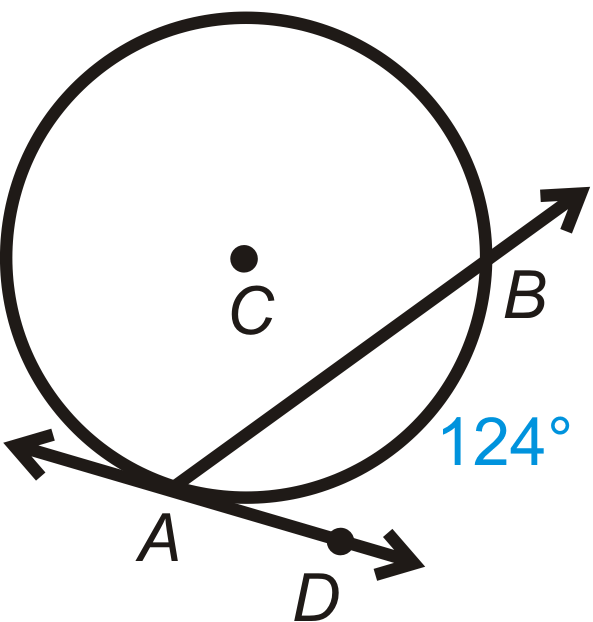
Рішення

Використовуйте теорему хорда/дотичного кута. $m\angle BAD=\dfrac{1}{2}m\widehat{AB}=\dfrac{1}{2}\cdot 124^{\circ}=62^{\circ}$.

Приклад$\PageIndex{4}$

Знайти$a$,$b$, і$c$.

Малюнок$\PageIndex{6}$

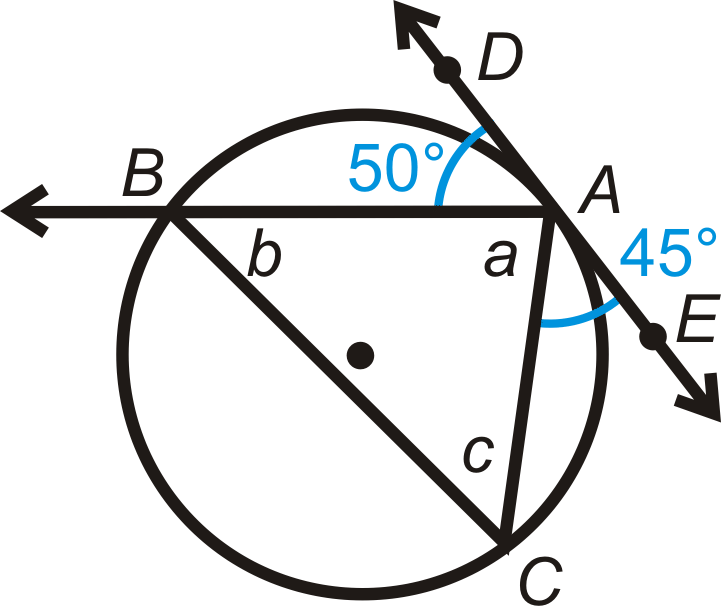
Рішення

\ (\ почати {масив} {c}
50^ {\ circ} +45^ {\ circ} +м\ кут a = 180^ {\ circ}\ квадратний\ текст {прямий кут}\\
m\ кут a=85^ {\ circ}\\
m\ кут b =\ frac {1} {2}\ cdot m\ widhat {A C}\
\ qquad\ почати {масив} {c}
\ widehat {A C} =2\ точка м\ кут E A C = 2\ cdot 45^ {\ circ} =90^ {\ circ}\\
м\ кут b =\ гідророзриву {1} {2}\ cdot 90^ {\ circ} =45^ {\ circ}
\ кінець {\ масив}\
85^ {\ circ} +45^ {\ circ} +м\ кут c = 180^ {\ circ}\ квад\ текст {Теорема про суму трикутника}\\
m\ кут c = 50^ {\ circ}
\ кінець {масив}\)

Приклад$\PageIndex{5}$

Знайти$m\widehat{AEB}$.

Малюнок$\PageIndex{7}$

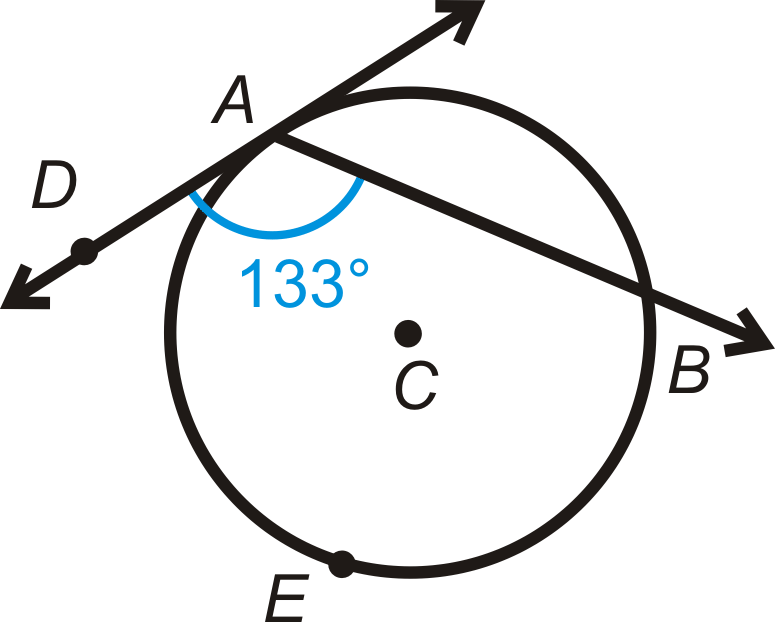
Рішення

Використовуйте теорему хорда/дотичного кута. $m\widehat{AEB}=2\cdot m\angle DAB=2\cdot 133^{\circ}=266^{\circ}.$

Рецензія

Знайти значення відсутньої змінної (ів).

1. 

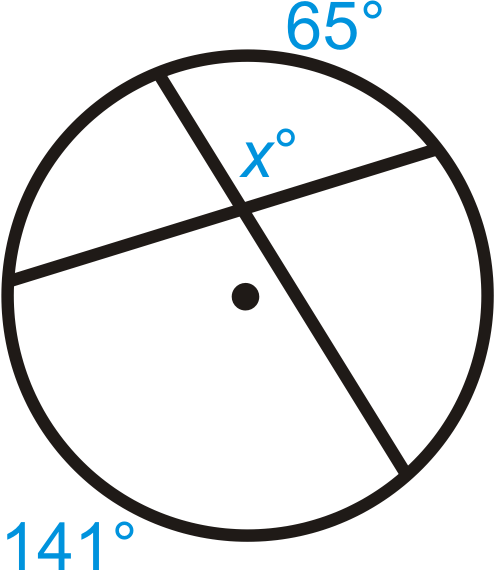
   Малюнок$\PageIndex{8}$

2. 

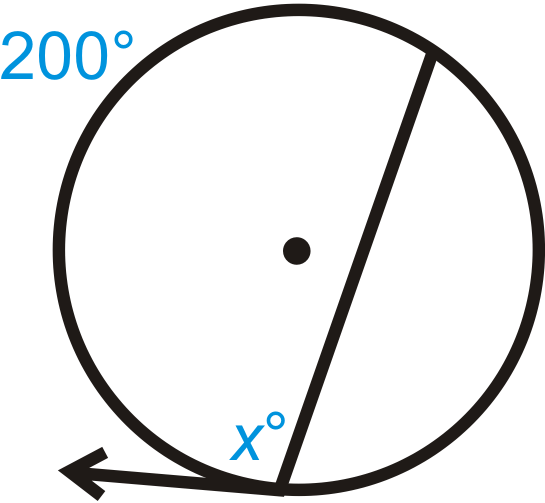
   Малюнок$\PageIndex{9}$

3. 

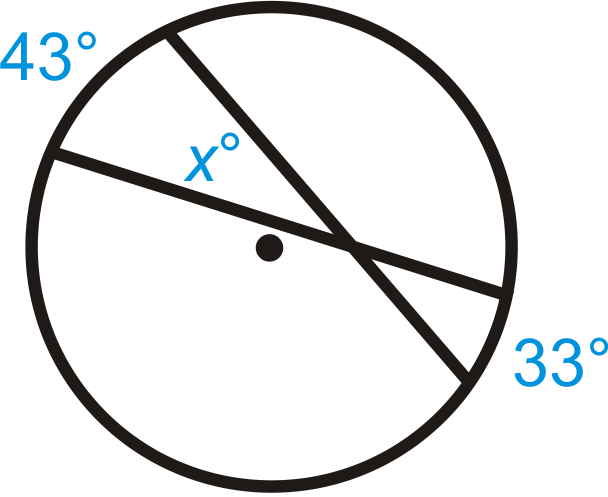
   Малюнок$\PageIndex{10}$

4. 

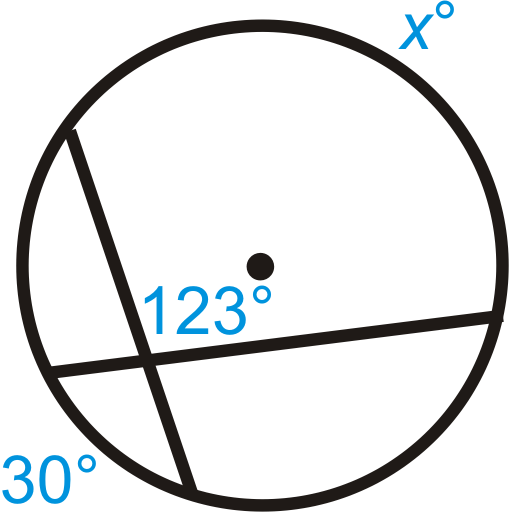
   Малюнок$\PageIndex{11}$

5. 

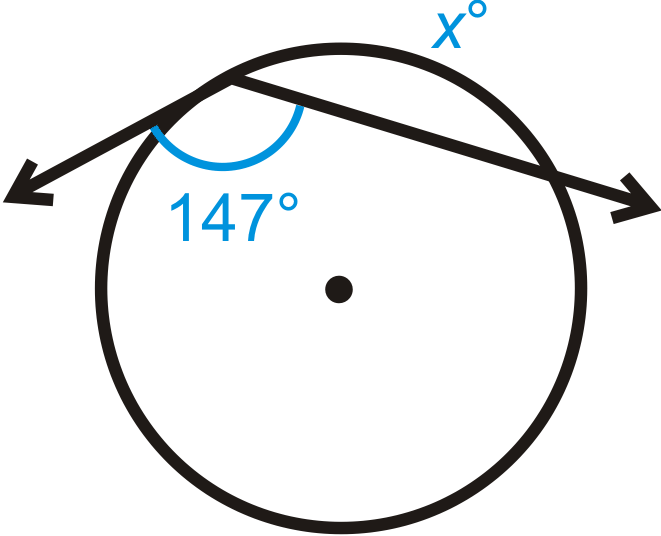
   Малюнок$\PageIndex{112}$

6. 

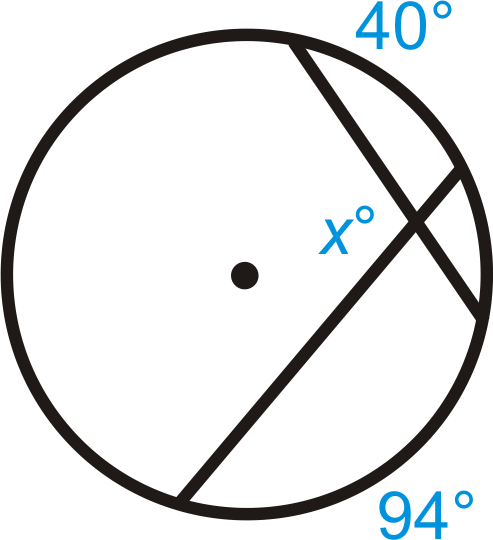
   Малюнок$\PageIndex{13}$

7. $y\neq 60^{\circ}$

   

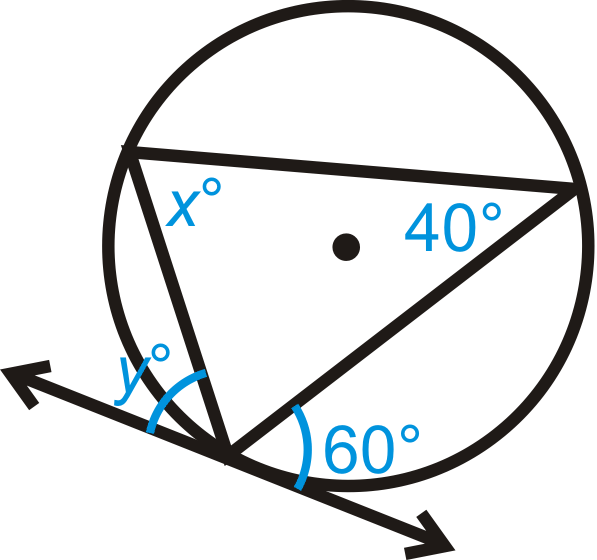
   Малюнок$\PageIndex{14}$

Вирішити для$x$.

8. Заповніть пробіли доказу для теореми кута перетинаються хорди

   

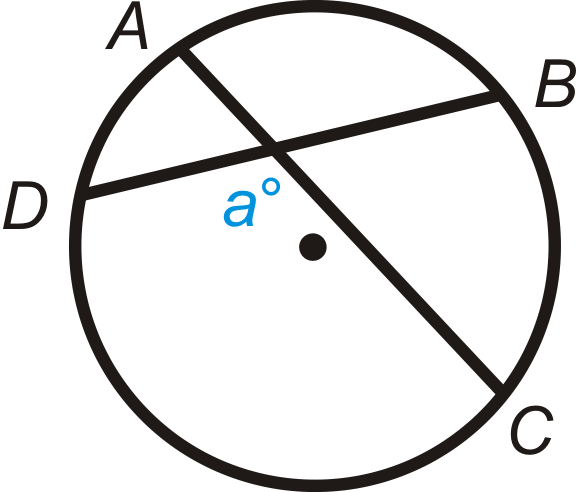
   Малюнок$\PageIndex{15}$

Дано: Перетинаються акорди$\overline{AC}$ і$\overline{BD}$.

Доведіть:$m\angle a=\dfrac{1}{2}(m\widehat{DC}+m\widehat{AB})$

Заява	Причина
1. Перетинаються акорди$\overline{AC}$ і$\overline{BD}$.	1.
2. Малювати$\overline{BC}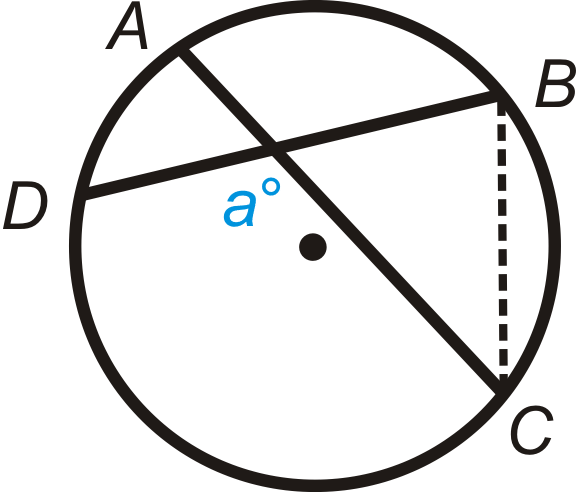$ Малюнок$\PageIndex{16}$	2. Будівництво
3. $m\angle DBC=\dfrac{1}{2}m\widehat{DC}$ $m\angle ACB=\dfrac{1}{2}m\widehat{AB}$	3.
4. $m\angle a=m\angle DBC+m\angle ACB$	4.
5. $m\angle a=\dfrac{1}{2}m\widehat{DC}+\dfrac{1}{2}m\widehat{AB}$	5.

Заповніть заготовки.

9. Якщо вершина кута дорівнює _______________ окружності, то її міра - середнє значення __________________ дуг.
10. Якщо вершина кута ________ коло, то її міра ______________ перехоплена дуга.

Лексика

Термін	Визначення
центральний кут	Кут, утворений двома радіусами і вершина якого знаходиться в центрі кола.
акорд	Відрізок лінії, кінцеві точки якого знаходяться на колі.
коло	Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
діаметр	Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
вписаний кут	Кут з його вершиною на колі і сторони якого є хордами.
перехоплена дуга	Дуга, яка знаходиться всередині вписаного кута і кінцеві точки якої знаходяться на куті.
точка дотику	Точка, де дотична лінія стосується кола.
радіус	Відстань від центру до зовнішнього обідка кола.
Теорема про хорду/дотичну кут	Теорема хорда/дотичного кута стверджує, що міра кута, утвореного хордою та тангенсом, що перетинаються на колі, є половиною міри перехопленої дуги.
Теорема кута, що перетинаються хорди	Теорема кута перетину хорд стверджує, що міра кута, утвореного двома хордами, які перетинаються всередині кола, є середньою мірою мір перехоплених дуг.

Додаткові ресурси

Інтерактивний елемент

Відео: Кути на і всередині кола принципи - основні

Діяльність: Кути на та всередині кола Питання обговорення

Навчальні посібники: Дуги та кути Навчальний посібник

Практика: Кути на колі та всередині