Skip to main content
LibreTexts - Ukrayinska

6.19: Теорема про перетинаються секанти

  1. Last updated
  2. Save as PDF
  • Page ID
    54499

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Довести і використовувати теореми, що включають лінії, які перетинають коло в двох точках.

    Сегменти з секантів

    Коли дві секанти перетинаються за межами кола, коло ділить секанти на відрізки, пропорційні один одному.

    Теорема про два сегменти секантів: Якщо дві секанти витягуються із загальної точки поза колом, а відрізки позначені, як показано нижче, то\(a(a+b)=c(c+d)\).

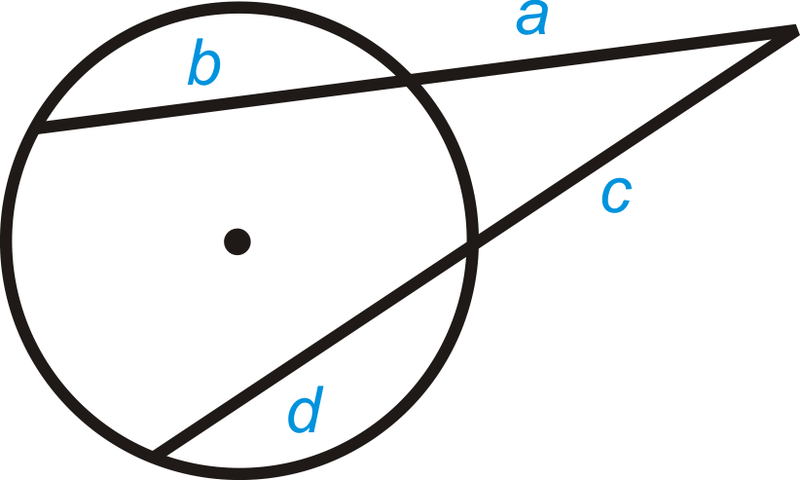
    Ф-д_5С8Е2ДД1С6С53923Б1Е1Ф49С68518 ФФФ 5Д554FF6A1Б638Б87ФД9Д+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Що робити, якщо вам дали коло з двома секантами, які перетинаються за межами кола? Як можна використовувати довжину деяких відрізків, утворених їх перетином, для визначення довжин невідомих відрізків?

    Приклад\(\PageIndex{1}\)

    Знайти\(x\). Спрощуйте будь-які радикали.

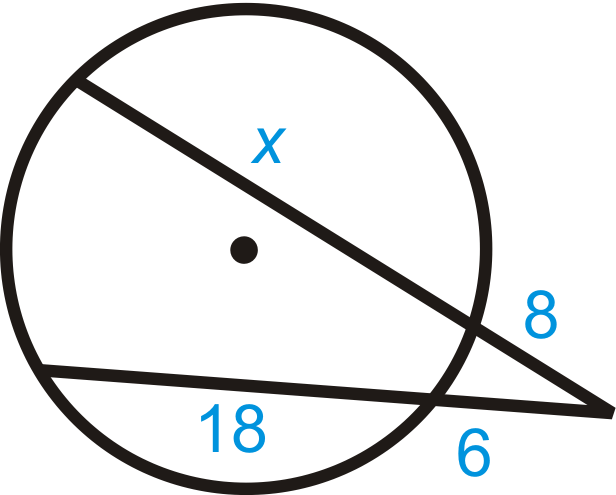
    F-д_БКСД 0Е619Е63048D8 ЕФБ925965А462ДК138С2С2 Бад 9540445D26 ADB+зображення_крихіткий+зображення_крихітка_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Використовуйте теорему про два сегменти секантів.

    \(\begin{aligned} 8(8+x)&=6(6+18) \\ 64+8x&=144 \\ 8x&=80 \\ x&=10\end{aligned}\)

    Приклад\(\PageIndex{2}\)

    Знайти\(x\). Спрощуйте будь-які радикали.

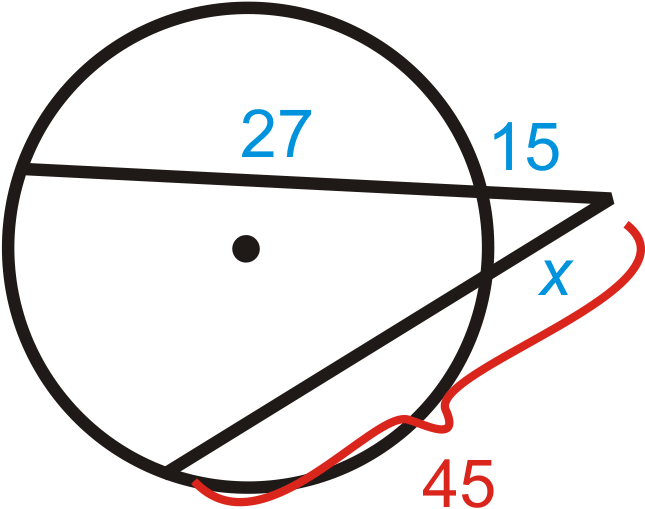
    Ф-Д_ААД 0БФ ФС0Ф 2FF766E0CF443 БКФ 67А 463 ЕЦФ9А01074FF49D6DCA2FD+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Використовуйте теорему про два сегменти секантів.

    \(\begin{aligned} 15(15+27)&=x\cdot45 \\ 630&=45x \\ x&=14 \end{aligned}\)

    Приклад\(\PageIndex{3}\)

    Знайдіть значення\(x\).

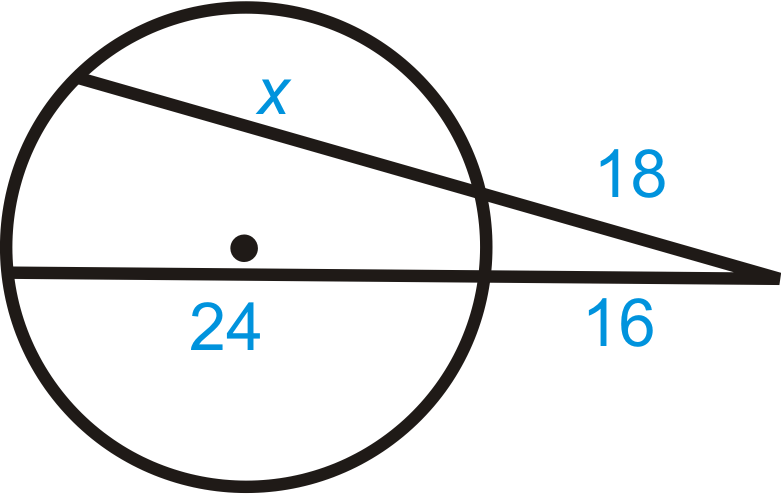
    Ф-Д_45БФ 07361ФБФ 28Б6929Б9Б5Ф41Е945Е3АФ9Б2 БК ЕДК 19081Е5Ф949+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Використовуйте теорему про два сегменти секантів.

    \(\begin{aligned}18\cdot(18+x)&=16\cdot(16+24) \\ 324+18x&=256+384 \\ 18x&=316 \\ x&=17\dfrac{5}{9}\end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Знайдіть значення\(x\).

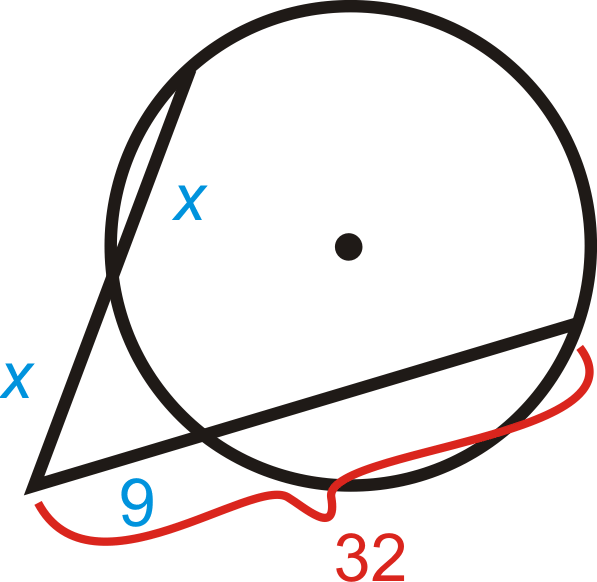
    F-D_D81721Д7А46АА7БД АФ 75388 подача 5Б1Ф2 ББ2ФФ 46А7А7А7АА24+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Використовуйте теорему про два сегменти секантів.

    \(\begin{aligned}x\cdot(x+x)&=9\cdot 32 \\ 2x^2&=288 \\ x^2&=144 \\ x&=12,\: x\neq −12 (\text{length is not negative})\end{aligned}\)

    Приклад\(\PageIndex{5}\)

    True або False: Дві секанти завжди перетинаються за межами кола.

    Рішення

    Помилкові. Якщо дві секанти паралельні, вони ніколи не перетинаються. Також можливо, щоб дві секанти перетиналися всередині кола.

    Рецензія

    Заповніть пропуски для кожної задачі нижче. Потім вирішуйте для відсутнього відрізка.

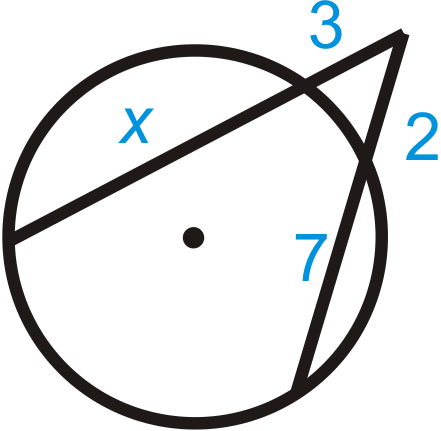
    1. F-д_52ЕД 8А05СБ8 ББД 6А4330ЕФ90 БДФ 533Б7623 ЕФБ17к4Ф0Е785А828522+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{6}\)

    \(3(\text{______}+\text{______})=2(2+7)\)

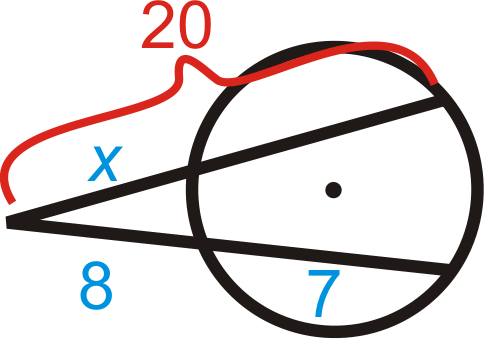
    1. F-д_D9149683898D5689D4D4E6B67460a8 ФЕФ0856EB1A812957A246C+зображення_крихіткий+зображення_крихіткий_png
      Малюнок\(\PageIndex{7}\)

    \(x\cdot\text{______}=8(\text{______}+\text{______})\)

    Знайдіть x на кожній діаграмі нижче. Спрощуйте будь-які радикали.

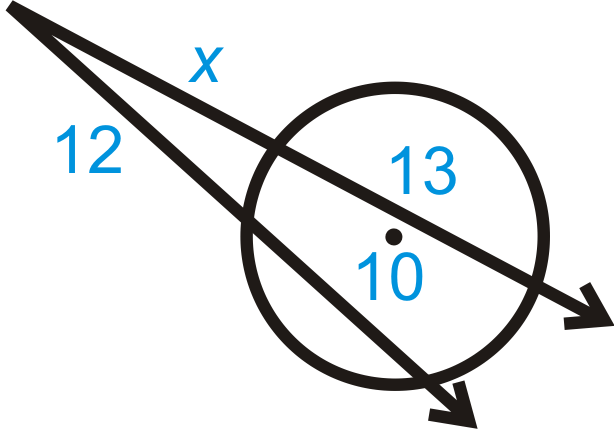
    1. Ф-Д_0БД 2608Д9С3Б9Б59ЕЦ5 Фе 0029018106DC 83BE69FE1A94371C1062+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
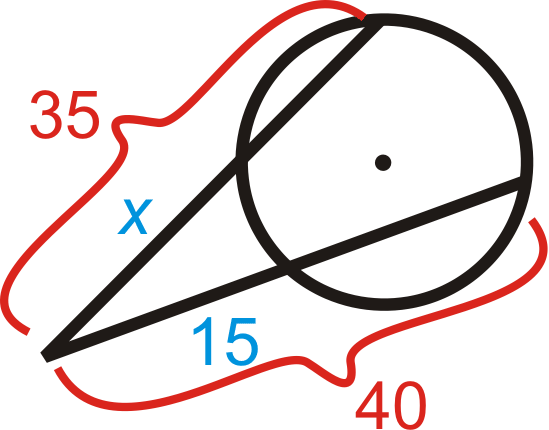
    2. F-D_D3746Б12ДБ3ДБ3Д4Ф915Е69БФЦ 6519 БЕ670233650Б3Д 94141CF5E355750+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
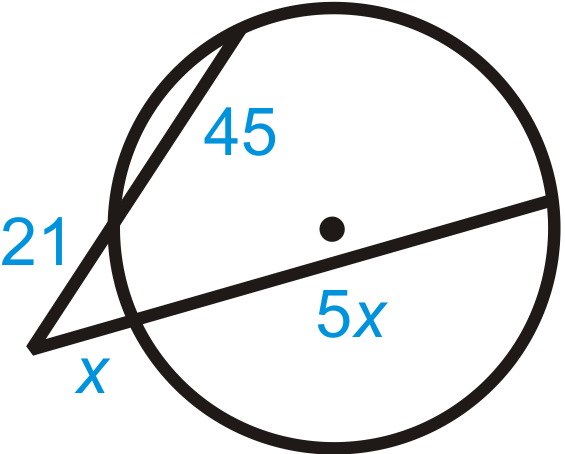
    3. Ф-Д_ЕК 9С65С26Е02ФА3 БК FF6ФББ4Б8ДК36800Б17С3Б002564E06BE7+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
    1. Заповніть пробіли доказу теореми про відрізки двох секантів.
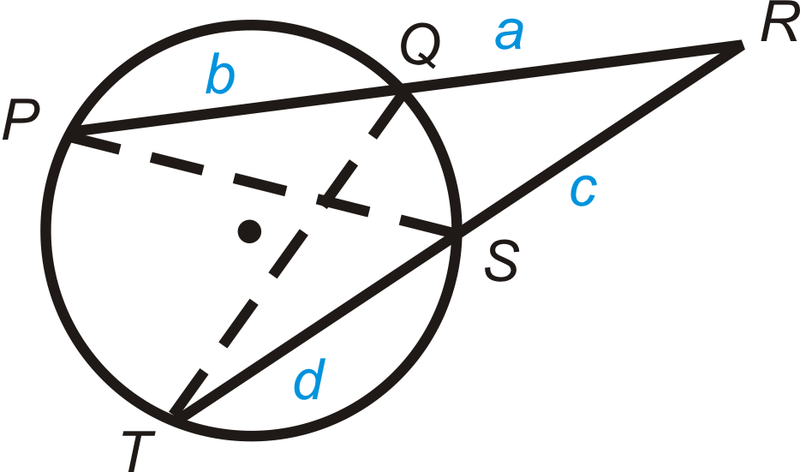
      F-D_7AD 886 Ф4С83ФБА 92Ф5С4023ФК 84А 9А39Ф2Е3АБ 5Ф161С6485ФФДДДД1+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)

    Дано: Секанти\(\overline{PR}\) і\(\overline{RT}\)

    Доведіть:\(a(a+b)=c(c+d)\)

    Заява Причина
    1. Секанти\(\overline{PR}\) і\(\overline{RT}\) з відрізками\(a\)\(b\),\(c\),, і\(d\). 1. Враховується
    2. \(\angle R\cong \angle R\) 2. Рефлексивний PoC
    3. \(\angle QPS\cong \angle STQ\) 3. Теорема про конгруентні вписані кути
    4. \(\Delta RPS\sim \Delta RTQ\) 4. Постулат подібності AA
    5. \(ac+d=ca+b\) 5. Відповідні частини подібних трикутників пропорційні
    6. \(a(a+b)=c(c+d)\) 6. перехресне множення

    Вирішити для невідомої змінної.

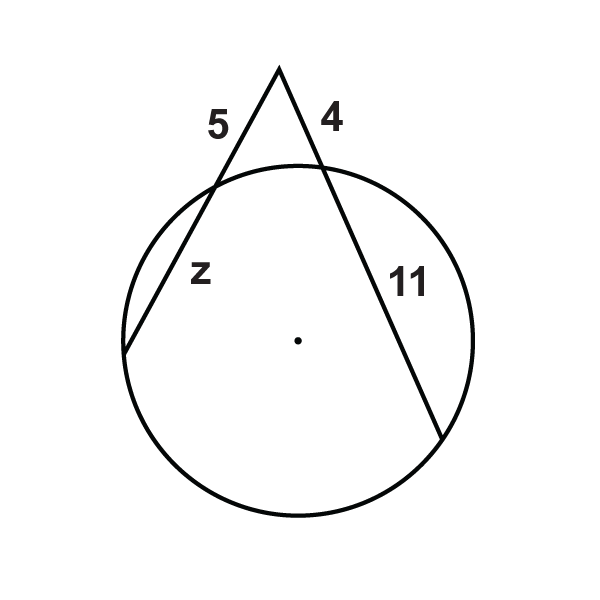
    1. F-D_23055 БА 6Д0Ф7Ф6Ф9АЕ6Б40Е5ЕА9Е36CF497C236ФД8309839 BBC 7D1+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
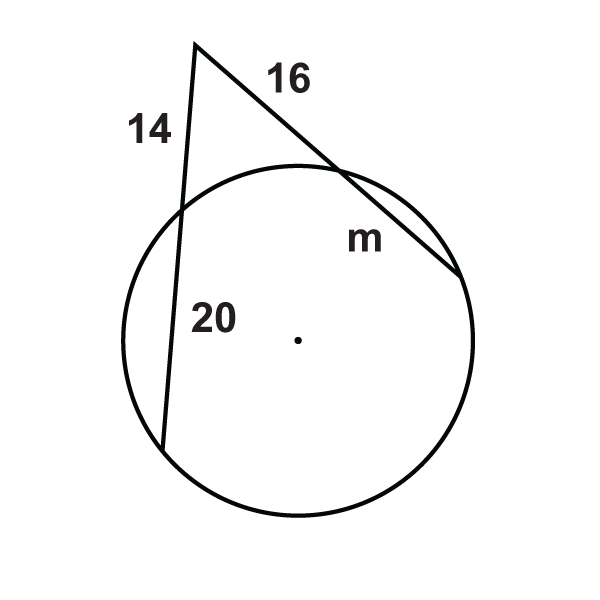
    2. F-Д_Д1 ФА3Д 89 ГК КА 35С4324Д115А 5БА0534 ФК8С1Ф205993Б9548Е89Д9753+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
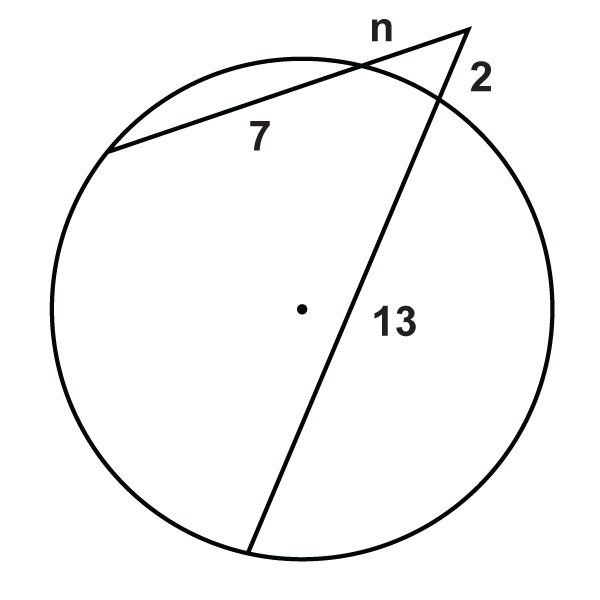
    3. F-D_C2C 2908C849 ФА8669Е 0 мертвий 84Bcd 25c9c3dc0c5530f22603863B31E6+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
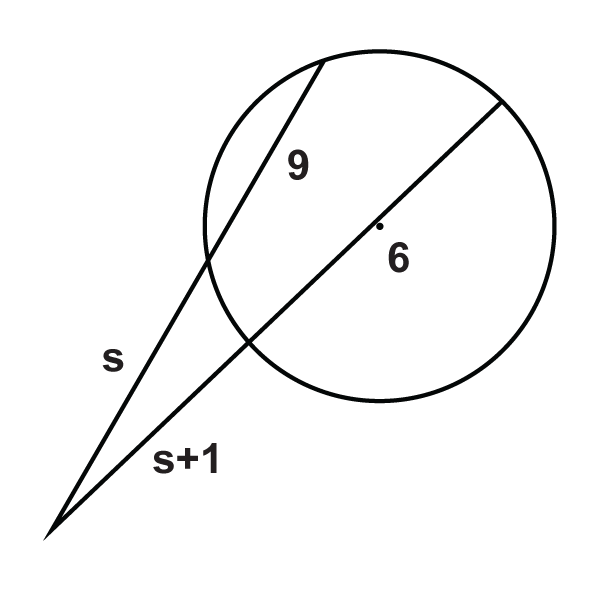
    4. F-D_20199408CE4C2E04CAD9191CDB БФ 83Ф857А8 ФЕ0А290ДФ93Д5А3С6Д1Е+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
    5. F-D_20199408CE4C2E04CAD9191CDB БФ 83Ф857А8 ФЕ0А290ДФ93Д5А3С6Д1Е+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
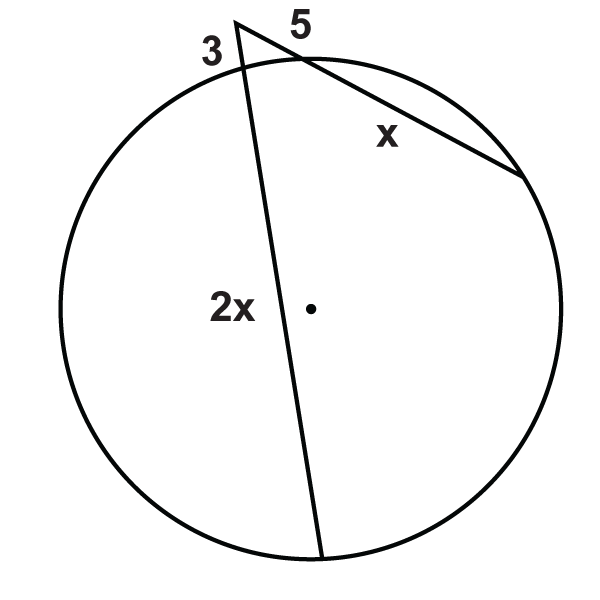
    6. Ф-д_Б1Б57Ф0404С95Д08Д 888355кБ44Д219А34ФФА062987 ЕД72С9Д2СБ4+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)
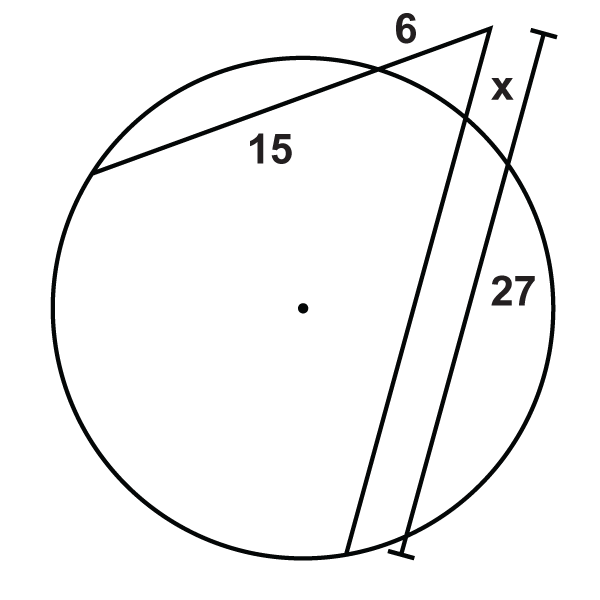
    7. Ф-д_7БДФ 150А 1721Е9ДФ 9дФ9Д3441д41 Каф3д 4030197909157802 куб фаа9+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)
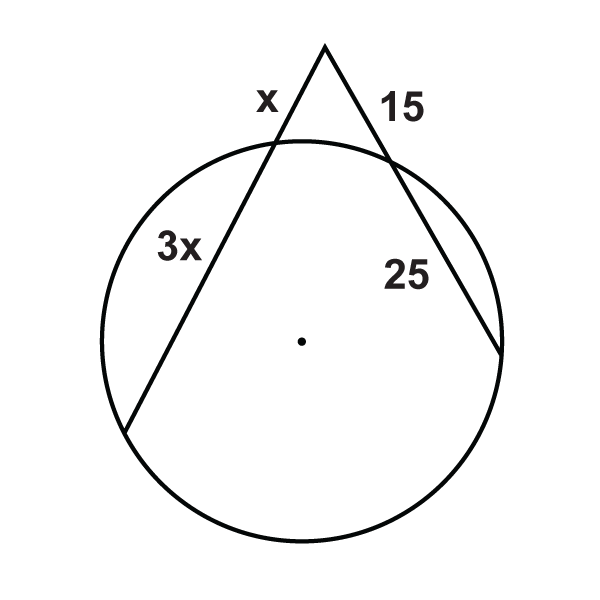
    8. Ф-д_27АФ 12441С3606С9Б4Б4Ф6Ф1А86А54А4Е45Б5БК0А40423268А27+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)
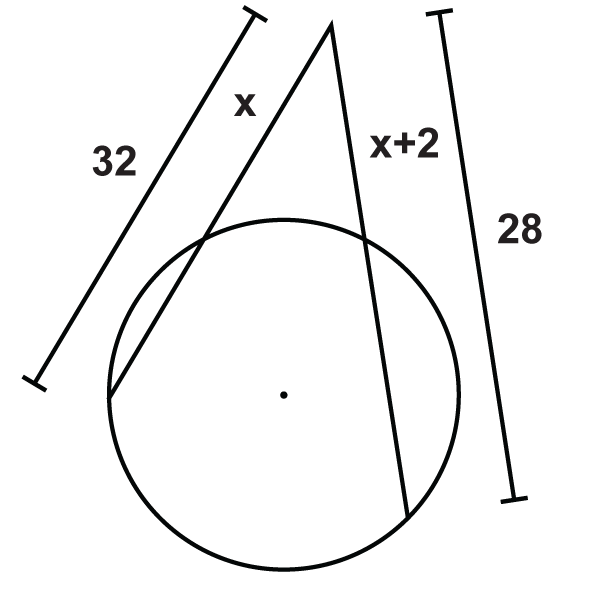
    9. F-D_B74C284E8E529266C592F9994D4D0EAC3DB1D9B1BF99A2874C2EF455+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 9.10.

    Лексика

    Термін Визначення
    центральний кут Кут, утворений двома радіусами і вершина якого знаходиться в центрі кола.
    акорд Відрізок лінії, кінцеві точки якого знаходяться на колі.
    коло Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    Вписаний кут Вписаний кут - це кут з його вершиною на колі. Міра вписаного кута - половина міри його перехопленої дуги.
    перехоплена дуга Дуга, яка знаходиться всередині вписаного кута і кінцеві точки якої знаходяться на куті.
    точка дотику Точка, де дотична лінія стосується кола.
    радіус Відстань від центру до зовнішнього обідка кола.
    Постулат подібності AA Якщо два кути в одному трикутнику конгруентні двом кутам в іншому трикутнику, то два трикутника схожі.
    Конгруентний Конгруентні фігури ідентичні за розміром, формою і мірою.
    Рефлексивне властивість конгруентності \(\overline{AB}\cong \overline{AB}\)або\(\angle B\cong \angle B\)
    Секантний Секанс кута в прямокутному трикутнику - це величина, знайдена діленням довжини гіпотенузи на довжину сторони, прилеглої до заданого кута. Відношення секанс - це зворотне косинусного відношення.
    січна лінія Січна лінія - це лінія, яка з'єднує дві точки на кривій.
    дотична лінія Дотична лінія - це лінія, яка «просто торкається» кривої в одній точці і ніякої іншої.
    Теорема про відрізки двох секантів Теорема про два відрізки секантів стверджує, що якщо ви маєте точку поза колом і намалюєте дві січні лінії від неї, існує зв'язок між утвореними відрізками лінії.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Сегменти з принципів секантів - Основні

    Діяльність: Сегменти з питань обговорення секантів

    Навчальні посібники: Кола: Сегменти та довжини навчальний посібник

    Практика: Теорема про перетинаються секанти