6.9: Дуги в колах

Last updated

Oct 27, 2022
Save as PDF
- 6.8: Радіус або діаметр окружності заданої площі
- 6.10: Площа секторів і сегментів

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Зрізи кола і центральних кутів.

Коло має $360^{\circ}$ . Дуга - це ділянка кола. Півколо - це дуга, яка вимірює $180^{\circ}$ .

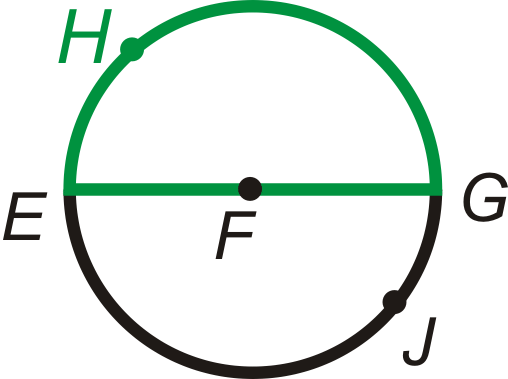
Ф-Д_07Б33Е1525А5Е51ФДБ 94ФДБ 94FF3АББ353БА83706Ф0ЕА 67198317F367+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

$\widehat{EHG}$ $\widehat{EJG}$ і півкола

Центральним кутом називається кут, утворений двома радіусами з його вершиною в центрі кола. Мінорна дуга - це дуга, яка менше $180^{\circ}$ . Велика дуга - це дуга, яка більше $180^{\circ}$ . Завжди використовуйте 3 літери для позначення великої дуги.

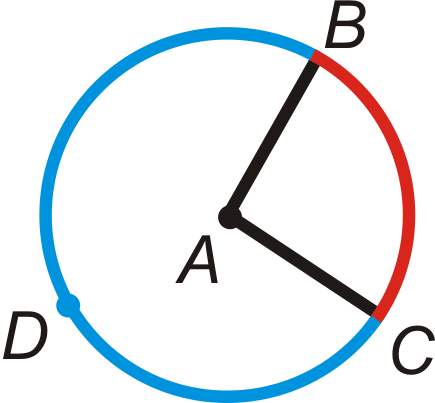
Ф-Д_5АААС 1БД2 ФА3224Е78Ф150 ААААА4Б46БФБ9Ф73Б1ББББ 0Ф26075C5FF+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{2}$

Центральний кут - це $\angle BAC$ . Мінорна дуга є $\widehat{BC}$ . Основна дуга є $\widehat{BDC}$ .

Дугу можна вимірювати в градусах або в лінійній мірі (см, фути і т.д.). У цьому понятті ми будемо використовувати ступінь міри. Міра другорядної дуги така ж, як і міра центрального кута, який їй відповідає. Міра великої дуги $360^{\circ}$ мінус міра відповідної другорядної дуги. Міра дуги, утвореної двома сусідніми дугами, є сумою мір двох дуг (Arc Addition Postulate).

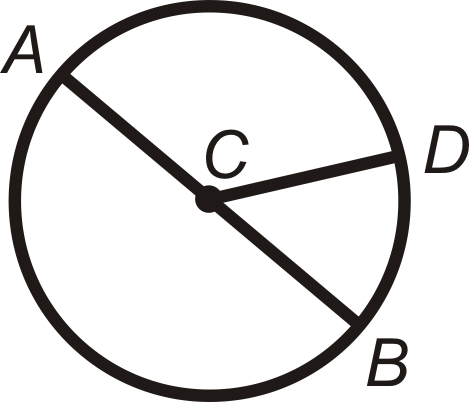
Ф-Д_КБА 8208898A5260D9D3001609DA34EF0CF89FDAE818255102E5E762+зображення_крихіткий+зображення_крихіткий_png — Малюнок $\PageIndex{3}$

$m\widehat{AD}+m\widehat{DB}=m\widehat{ADB}$

Що робити, якщо коло розділили на частини різними радіусами? Як ви могли знайти міри дуг, утворених цими радіусами?

Приклад $\PageIndex{1}$

Знайти $m\widehat{AB}$ і $m\widehat{ADB}$ в $\bigodot C$ .

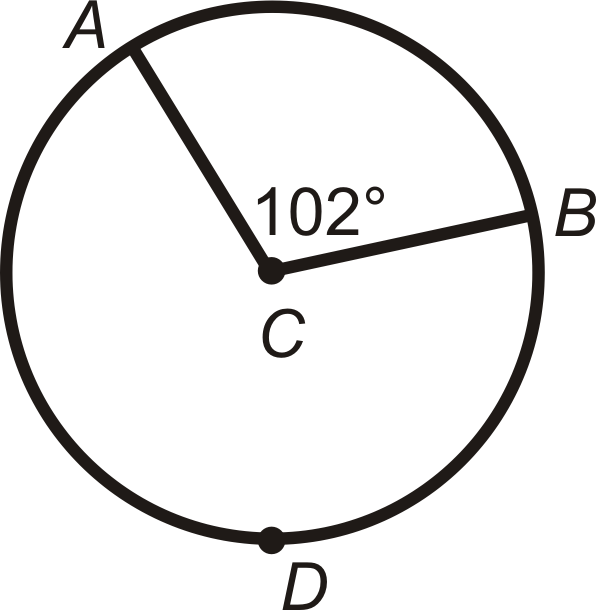
F-д_9Б9Д2Д06071920С9408ЦБА 9Е9Б940Е1937Д5ЕЕ075Б17Ф73С0389+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{4}$

Рішення

$m\widehat{AB}=m\angle ACB$ . Отже, $m\widehat{AB}=102^{\circ}$ .

$m\widehat{ADB}=360^{\circ}−m\widehat{AB}=360^{\circ}−102^{\circ}=258^{\circ}$

Приклад $\PageIndex{2}$

Знайдіть міри другорядних дуг в $\bigodot A$ . $\overline{EB}$ є діаметром.

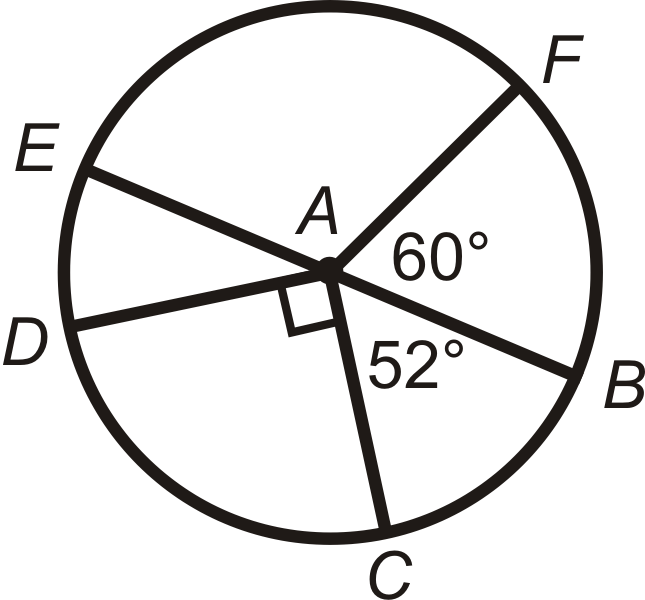
F-D15671635C9270833А949ДФА6352Е94ЕАФ 08396896Ф6243Б16+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{5}$

Рішення

Тому $\overline{EB}$ що це діаметр, $m\angle EAB=180^{\circ}$ . Кожна дуга має таку ж міру, як і її відповідний центральний кут.

$\begin{aligned} m\widehat{BF}&=m\angle FAB=60^{\circ} \\ m\widehat{EF}&=m\angle EAF=120^{\circ}\rightarrow 180^{\circ}−60^{\circ} \\ m\widehat{ED}&=m\angle EAD=38^{\circ} \rightarrow 180^{\circ}−90^{\circ}−52^{\circ} \\ m\widehat{DC}&=m\angle DAC=90^{\circ} \\ m\widehat{BC}&=m\angle BAC=52^{\circ}\end{aligned}$

Приклад $\PageIndex{3}$

Знайти мірки зазначених дуг в $\bigodot A$ . $\overline{EB}$ є діаметром.

Використовуйте постулат додавання дуги.

$m\widehat{FED}$
$m\widehat{CDF}$
$m\widehat{DFC}$

Рішення

$m\widehat{FED}=m\widehat{FE}+m\widehat{ED}=120^{\circ}+38^{\circ}=158^{\circ}$
$m\widehat{CDF}=m\widehat{CD}+m\widehat{DE}+m\widehat{EF}=90^{\circ}+38^{\circ}+120^{\circ}=248^{\circ}$
$m\widehat{DFC}=m\widehat{ED}+m\widehat{EF}+m\widehat{FB}+m\widehat{BC}=38^{\circ}+120^{\circ}+60^{\circ}+52^{\circ}=270^{\circ}$

Приклад $\PageIndex{4}$

Перелічіть конгруентні дуги $\bigodot C$ нижче. $\overline{AB}$ і $\overline{DE}$ є діаметрами.

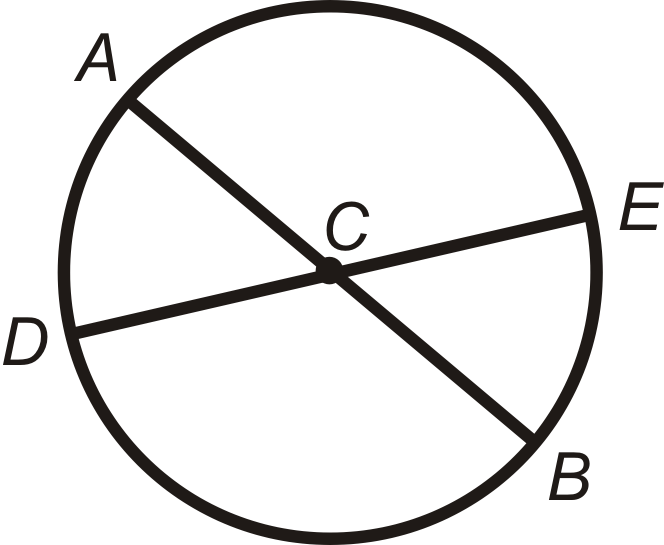
F-D_55AFD8D60444DB12686108CFE 0 CFD28154086A6 А3 А3А3Б820С1710+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{7}$

Рішення

$\angle ACD\cong \angle ECB$ тому що вони є вертикальними кутами. $\angle DCB\cong \angle ACE$ тому що вони також є вертикальними кутами.

$\widehat{AD}\cong \widehat{EB}$ і $\widehat{AE}\cong \widehat{DB}$

Приклад $\PageIndex{5}$

Для кожного з кіл нижче, сині дуги збігаються? Поясніть, чому чи чому ні.

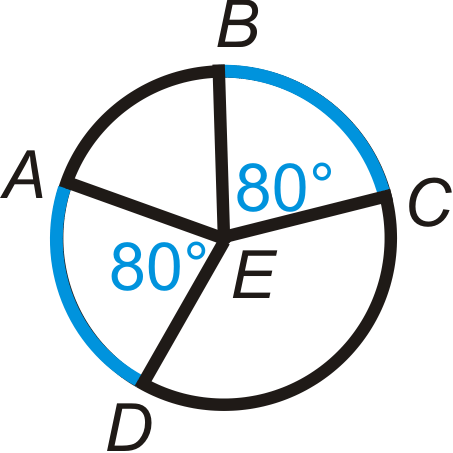
F-D_87D77CFFE 336E126E74D75C52ФБ64Д0Б2ФАА984 ББ5 CF76174DCFB333+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{8}$

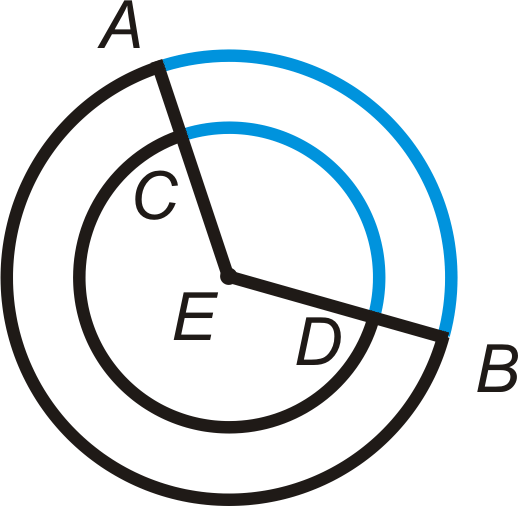
F-д_7897Е10С46ФА93061С1Б8ЕБ9Д92ДК87475105Е3269ДКА290Ф62ЕЕЕ25+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{9}$

Рішення

Для першого кола, $\widehat{AD}\cong \widehat{BC}$ тому що вони мають однаковий центральний кут вимірювання і знаходяться в одному колі.

Для другого кола дві дуги мають однакову міру, але не є конгруентними, оскільки кола мають різні радіуси.

Рецензія

Визначте, чи дуги нижче є незначною дугою, великою дугою або півколом $\bigodot G$ . $\overline{EB}$ є діаметром.

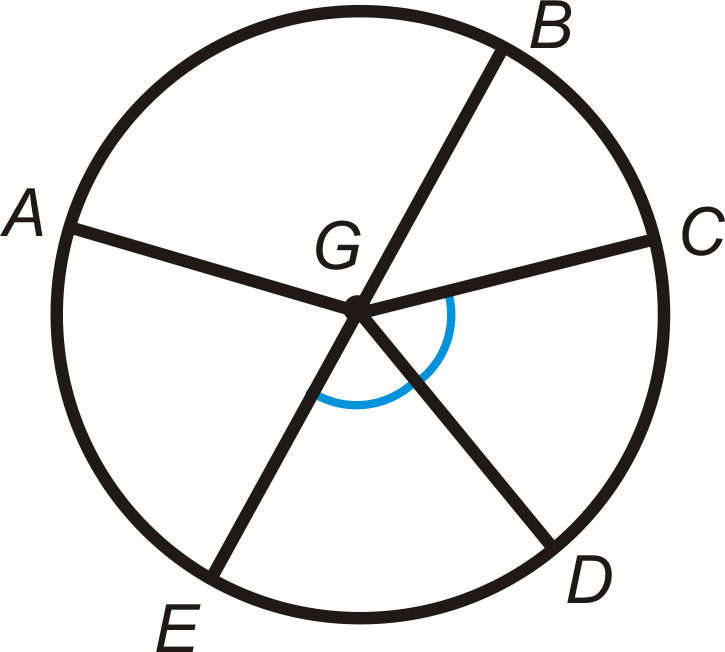
F-д_31БФ 1БФ ФД 00Б256Ф9Д1Ф5ЕЦБ70ЕД 49БАФ 455c6730001829b8579053E+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{10}$

$\widehat{AB}$
$\widehat{ABD}$
$\widehat{BCE}$
$\widehat{CAE}$
$\widehat{ABC}$
$\widehat{EAB}$
Чи є конгруентні дуги? Якщо так, перерахуйте їх.
Якщо $m\widehat{BC}=48^{\circ}$ , знайдіть m\ widehat {CD}\).
Використовуючи #8, знайдіть m\ widehat {CAE}\).

Знайдіть міру другорядної дуги та великої дуги в кожному колі нижче.

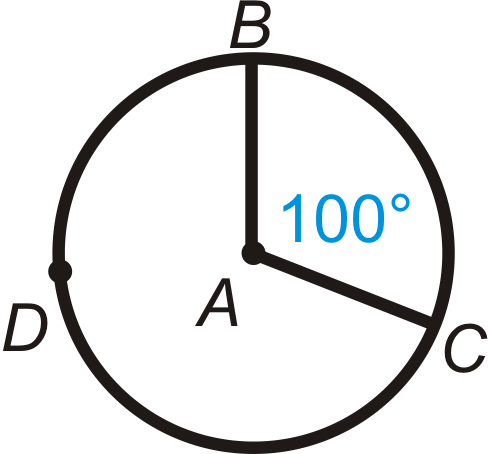
Малюнок $\PageIndex{11}$
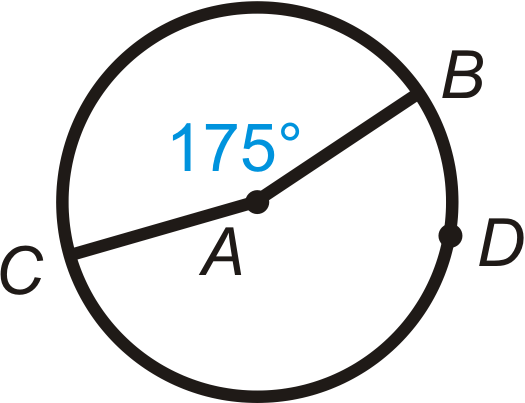
Малюнок $\PageIndex{12}$
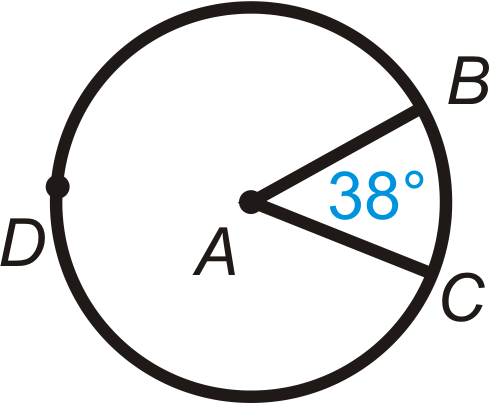
Малюнок $\PageIndex{13}$
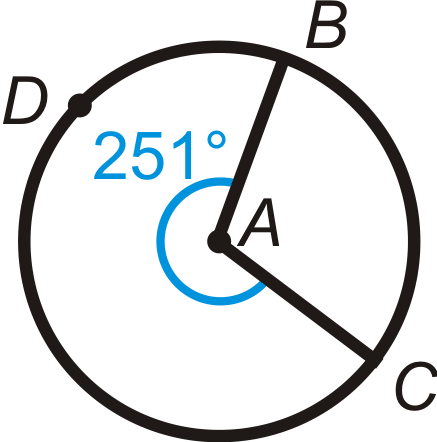
Малюнок $\PageIndex{14}$
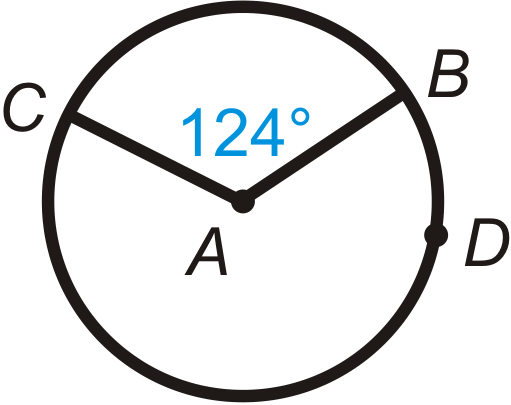
Малюнок $\PageIndex{15}$
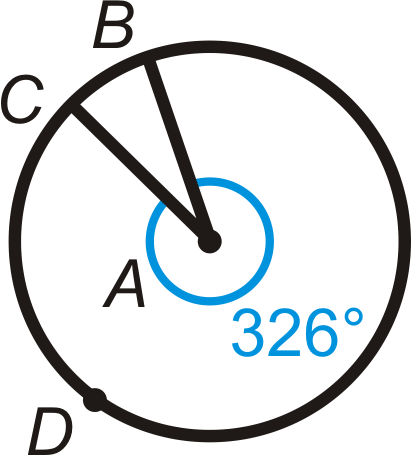
Малюнок $\PageIndex{16}$

Визначте, чи конгруентні сині дуги. Якщо так, то констатуйте чому.

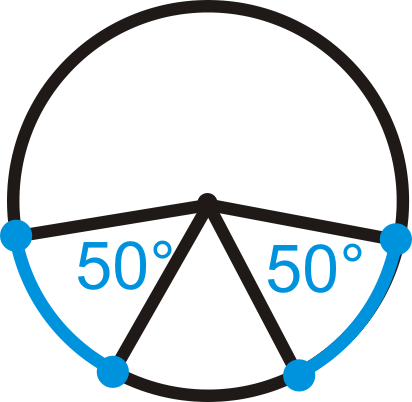
Малюнок $\PageIndex{17}$

Малюнок $\PageIndex{17}$

Малюнок $\PageIndex{17}$

Знайти міру зазначених дуг або центральних кутів в\ bigodot A\). \ overline {DG}\) - діаметр.

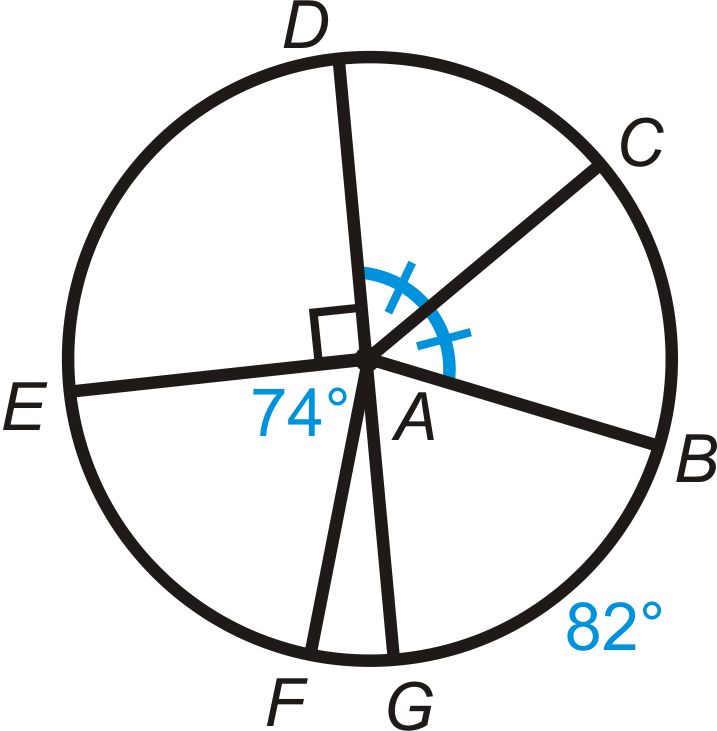
F-D_33 АД БА 7Д5Б3Е4АА11С1А66ФБ870А486476ЕБ5А44Е9С34ДК1681+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{18}$

\ широкий капелюх {DE}\)
\ широкий капелюх {DC}\)
\ широкий капелюх {GAB}\)
\ широка шапка {FG}\)
\ широкий капелюх {EDB}
\ широка шапка {EAB}\)
\ широкий капелюх {DCF}\)
\ широка шапка {DBE}\)

Знайти міру х\) в\ бігодо Р\).

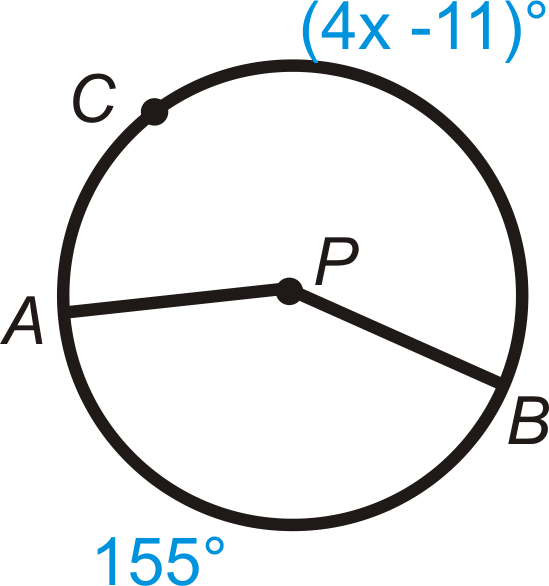
Малюнок $\PageIndex{19}$
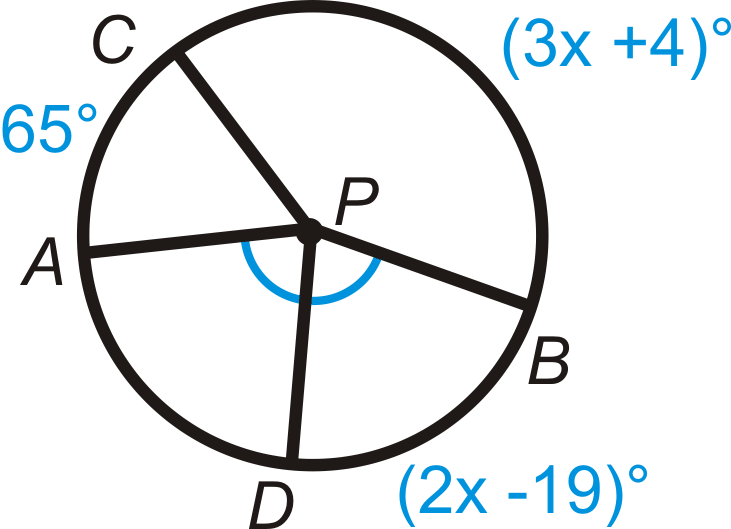
Малюнок $\PageIndex{20}$
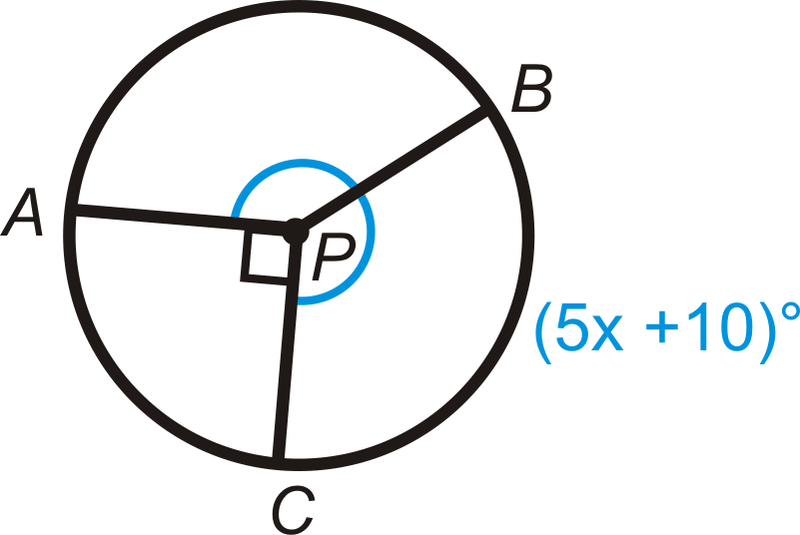
Малюнок $\PageIndex{21}$

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 9.3.

Лексика

Термін	Визначення
дуга	Єдина ділянка кола, що описує певний кут.
центральний кут	Кут, утворений двома радіусами і вершина якого знаходиться в центрі кола.
коло	Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається *центром*.
велика дуга	Дуга, яка більше $180^{\circ}$ .
незначна дуга	Дуга, яка менше $180^{\circ}$ .
радіус	Відстань від центру до зовнішнього обідка кола.
півколо	Дуга, яка вимірює $180^{\circ}$ .
Постулат додавання дуги	Постулат складання дуги стверджує, що міра дуги, утвореної двома сусідніми дугами, є сумою мір двох дуг.
Діаметр	Діаметр - це міра відстані через центр кола. Діаметр дорівнює подвоєної мірі радіуса.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи дуг в колах - Основні

Види діяльності: Дуги в колах Дискусійні питання

Навчальні посібники: властивості кола навчальний посібник

Практика: Дуги в колах

Реальний світ: Сільське господарство дуги