Skip to main content
LibreTexts - Ukrayinska

6.4: Окружність

  1. Last updated
  2. Save as PDF
  • Page ID
    54429

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Знайти окружність кола за формулами:\(C = \pi d\);\(C = 2\pi r\).

    Окружність - це відстань по колу. Окружність також можна назвати периметром кола. Однак ми використовуємо термін окружність для кіл, оскільки вони круглі.

    Формула окружності:\(C=\pi d\) де діаметр\(d=2r\), або подвійний радіус. Так\(C=2\pi r\) само, як і.

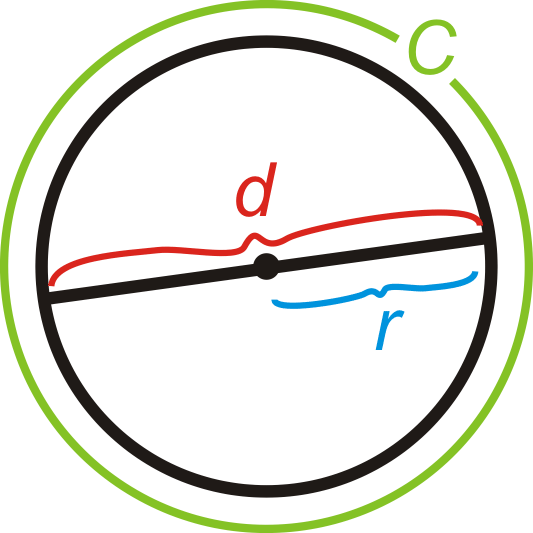
    Ф-Д_0ФК 20Ф33КК1С811513Е58Д048АА96ББ 40ЕЕЕЕЕ958901 BA98A06F1AA2C+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    \(\pi\), Або «пі» - відношення окружності кола до його діаметру. Вона приблизно дорівнює 3,14159265358979323846...

    У вас повинна бути кнопка\ pi на калькуляторі. Якщо ви цього не зробите, ви можете використовувати 3.14 як наближення для\(\pi\). Ви також можете залишити свої відповіді з точки зору\(\pi\) багатьох проблем.

    Що робити, якщо вам дали радіус або діаметр кола? Як ви могли знайти відстань навколо цього кола?

    Приклад\(\PageIndex{1}\)

    Знайдіть окружність кола радіусом 7 см.

    Рішення

    Вставте радіус в формулу.

    \(C=2\pi (7)=14\pi \approx 44\text{ cm }\)

    Приклад\(\PageIndex{2}\)

    Окружність кола -\(64\pi\) одиниці. Знайдіть діаметр.

    Рішення

    Знову ж таки, ви можете підключити те, що ви знаєте, у формулу окружності та вирішити для\(d\).

    \(\begin{aligned} 64\pi =\pi d \\ 64\text{ units }=d\end{aligned}\)

    Приклад\(\PageIndex{3}\)

    Коло вписується в квадрат з 10 ст. сторонами. Що таке окружність кола? Залиште свою відповідь з точки зору\(\pi\).

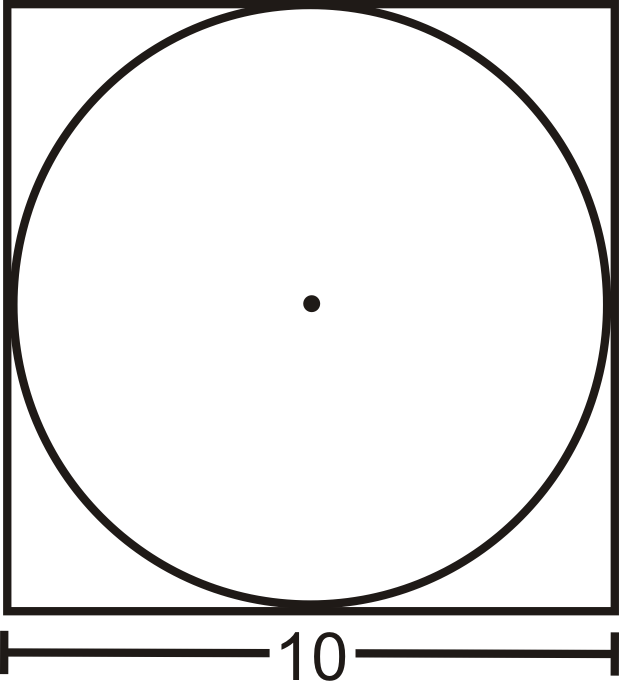
    F-д_Ф5374 Баа 682А4 ДД2126Б580А7ФД6Ф5С2ДФ5КФ 74ЕФ1779АА7+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    З малюнка ми бачимо, що діаметр кола дорівнює довжині сторони. \(C=10\pi \text{ in. }\)

    Приклад\(\PageIndex{4}\)

    Знайдіть периметр квадрата в прикладі 3. Це більше або менше окружності кола? Чому?

    Рішення

    Периметр. Для\(P=4(10)=40\text{ in. }\) того, щоб порівняти периметр з окружністю, ми повинні змінити окружність на десяткову.

    \(C=10\pi \approx 31.42 \text{ in. }\)Це менше периметра квадрата, що має сенс, оскільки коло знаходиться всередині квадрата.

    Приклад\(\PageIndex{5}\)

    Шини на компактному автомобілі мають діаметр 18 дюймів. Як далеко їде автомобіль після того, як покришки повертаються один раз? Як далеко проїжджає машина після 2500 обертань шин?

    F-D_DA1da223cb015e51d37c4dcc8c5590b335dfdf9bc9bc7534fe545e+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Один оборот покришки - це окружність. Це було б\(C=18\pi \approx 56.55\text{ in. }\) 2500 обертань буде\(2500\cdot 56.55\) приблизно 141,375 дюйма, 11,781 футів, або 2.23 миль.

    Рецензія

    Заповніть наступну таблицю. Залиште всі відповіді в плані\(\pi\).

    діаметр радіус окружність
    1. 15
    2. 4
    3. 6
    4. \(84\pi\)
    5. 9
    6. \(25\pi\)
    7. \(2\pi\)
    8. 36
    1. Знайдіть окружність кола с\(d=\dfrac{20}{\pi} \text{ cm }\).

    \(PQSR\)Квадрат вписаний в\(\bigodot T\). \(RS=8\sqrt{2}\).

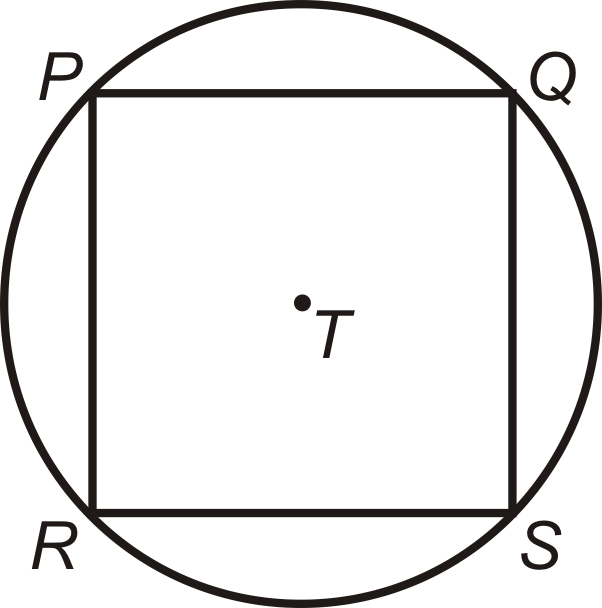
    F-д_4Б0БФ6А1АЕС528ФБ3260Ф54КД0Е 350 Е1186063414837Ф1252Б0ЕФ322+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)
    1. Знайти довжину діаметра\(\bigodot T\).
    2. Як співвідноситься діаметр\(PQSR\)?
    3. Знайдіть периметр\(PQSR\).
    4. Знайдіть окружність\(\bigodot T\).

    Для питань 14-17 вантажівка має шини діаметром 26.

    1. Як далеко їде вантажівка кожного разу, коли шина повертається рівно один раз? Що це таке ж, як?
    2. Скільки разів шина повернеться після того, як вантажівка проїде 1 милю? (1 миля = 5280 футів)
    3. Вантажівка пройшла 4072 обертання шин. Скільки це миль?
    4. Середня рекомендація щодо терміну служби шини становить 30 000 миль. Скільки обертань це?

    Лексика

    Термін Визначення
    акорд Відрізок лінії, кінцеві точки якого знаходяться на колі.
    коло Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
    Окружність Окружність кола - це міра відстані навколо зовнішнього краю кола.
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    пі (Або\(\pi\)) Відношення окружності кола до його діаметру.
    Радіус Радіус кола - це відстань від центру кола до краю кола.
    Конгруентний Конгруентні фігури ідентичні за розміром, формою і мірою.
    Звичайний багатокутник Правильний багатокутник - це багатокутник з усіма сторонами однакової довжини і всіма кутами однаковою мірою.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Окружність кола

    Діяльність: Питання обговорення окружності

    Навчальні посібники: Навчальний посібник з окружності та довжини

    Практика: Окружність

    Реальний світ: обхідний шлях додому