6.21: Кола в координатній площині

Графік кола. Використовуйте$(h, k)$ як центр, так і точку на колі. Формула:$(x-h)^2 + (y-k)^2 = r^2$$(h, k)$ де центр і$r$ радіус.

Нагадаємо, що коло - це сукупність всіх точок на площині, які знаходяться на однаковій відстані від центру. Це визначення може бути використано для пошуку рівняння кола в координатній площині.

Малюнок$\PageIndex{1}$

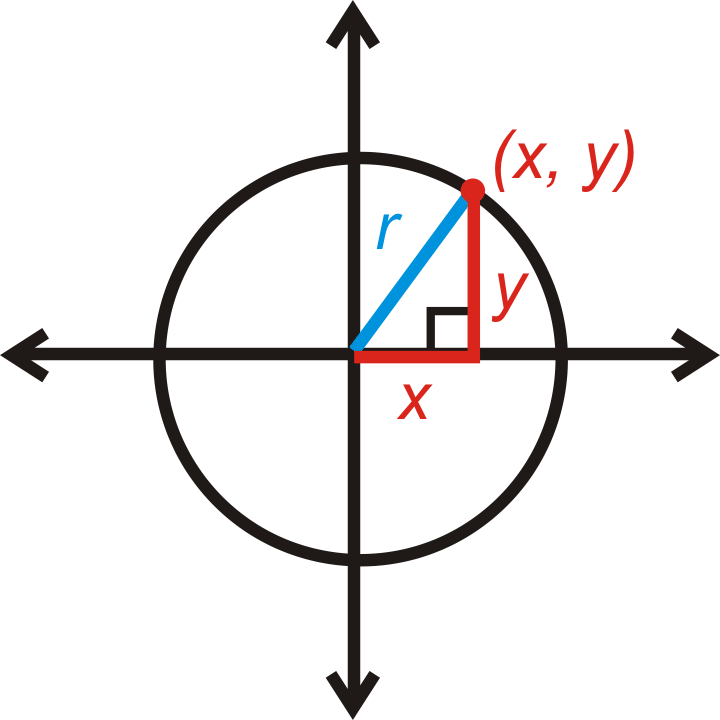
Почнемо з кола по центру$(0, 0)$. Якщо$(x,y)$ точка на колі, то відстань від центру до цієї точки буде радіусом, r. x - відстань по горизонталі, а y - відстань по вертикалі. Це утворює прямокутний трикутник. З теореми Піфагора рівняння кола, зосередженого на початку, є$x^2+y^2=r^2$.

Центр не завжди повинен бути включеним$(0, 0)$. Якщо його немає, то маркуємо центр$(h,k)$. Потім ми використаємо формулу відстані, щоб знайти довжину радіуса.

Малюнок$\PageIndex{2}$

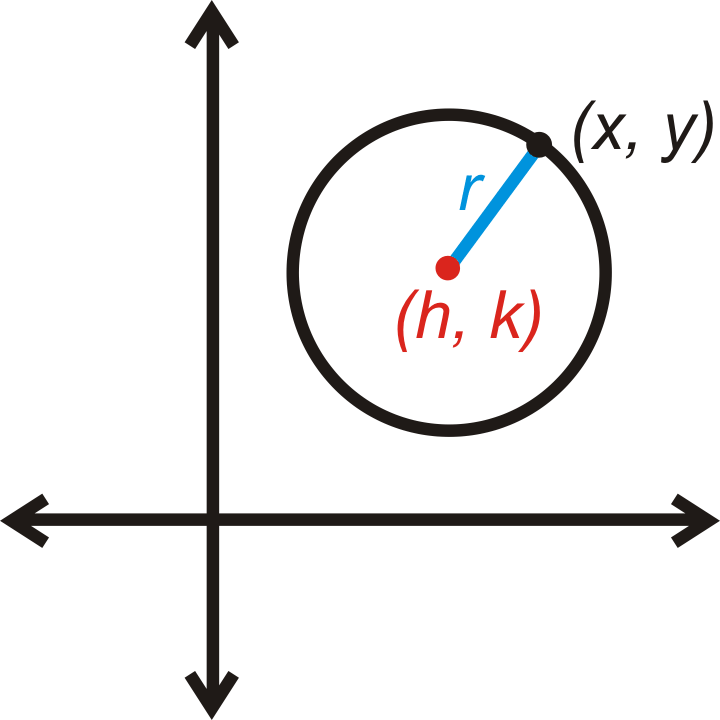
$r=\sqrt{(x−h)^2+(y−k)^2}$

Якщо ви квадратуєте обидві сторони цього рівняння, то у вас буде стандартне рівняння кола. Стандартне рівняння кола з центром$(h,k)$ і радіусом$r$ є$r^2=(x−h)^2+(y−k)^2$.

Що робити, якщо вам дали довжину радіуса кола і координати його центру? Як ви могли записати рівняння кола в координатній площині?

Приклад$\PageIndex{1}$

Знайдіть центр і радіус наступного кола.

$(x+2)^2+(y−5)^2=49$

Рішення

Перепишіть рівняння як$(x−(−2))^2+(y−5)^2=7^2$. Центром є$(-2, 5)$ і$r=7$.

Майте на увазі, що через мінусових знаків у формулі координати центру мають протилежні ознаки того, якими вони можуть спочатку здаватися.

Приклад$\PageIndex{2}$

Знайдіть центр і радіус наступного кола.

Знайдіть рівняння кола з центром$(4, -1)$ і яке проходить$(-1, 2)$.

Рішення

Спочатку підключіть до центру стандартне рівняння.

$\begin{aligned} (x−4)^2+(y−(−1))^2&=r^2 \\ (x−4)^2+(y+1)^2&=r^2\end{aligned}$

Тепер підключіть (-1, 2) для$x$$y$ і вирішуйте для$r$.

$\begin{aligned} (−1−4)^2+(2+1)^2=r^2 \\ (−5)^2+(3)^2&=r^2 \\ 25+9&=r^2 \\ 34&=r^2\end{aligned}$

Підставляючи в$34$ for$r^2$, рівняння є$(x−4)^2+(y+1)^2=34$.

Приклад$\PageIndex{3}$

Графік$x^2+y^2=9$.

Рішення

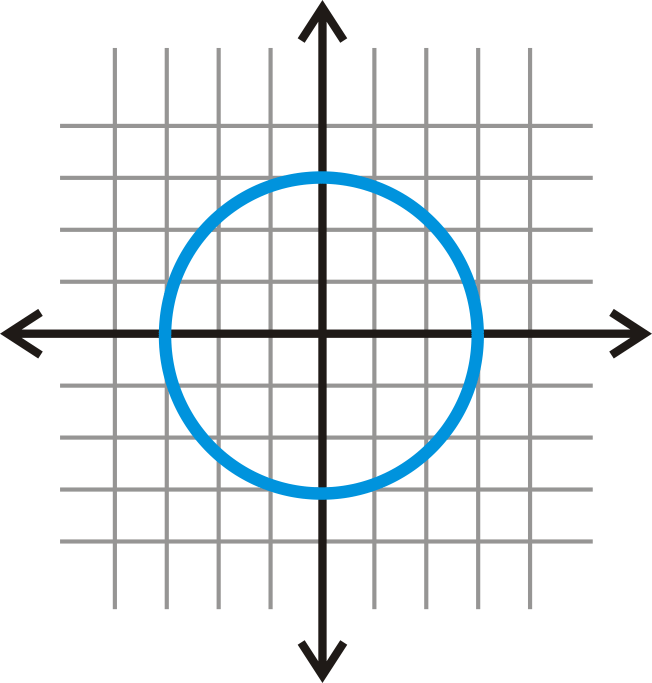
Центр - це$(0, 0)$. Його радіус - квадратний корінь з 9, або 3. Помістіть центр, побудуйте точки, які є 3 одиницями вправо, вліво, вгору і вниз від центру, а потім з'єднайте ці чотири точки, щоб сформувати коло.

Малюнок$\PageIndex{3}$

Приклад$\PageIndex{4$

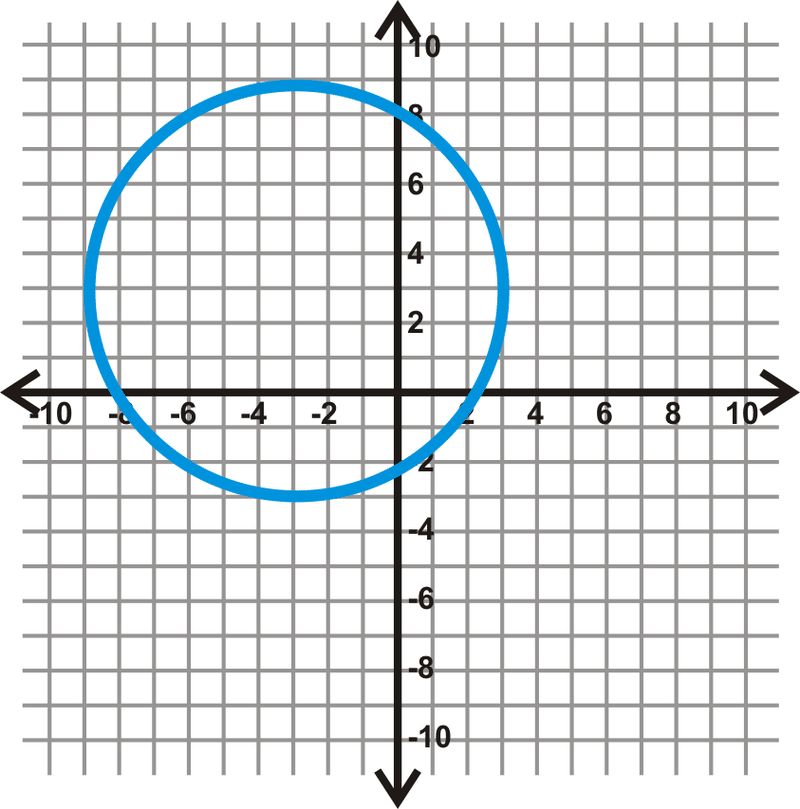
Знайдіть рівняння кола нижче.

Малюнок$\PageIndex{4}$

Рішення

Спочатку знайдіть центр. Намалюйте горизонтальний і вертикальний діаметри, щоб побачити, де вони перетинаються.

Малюнок$\PageIndex{5}$

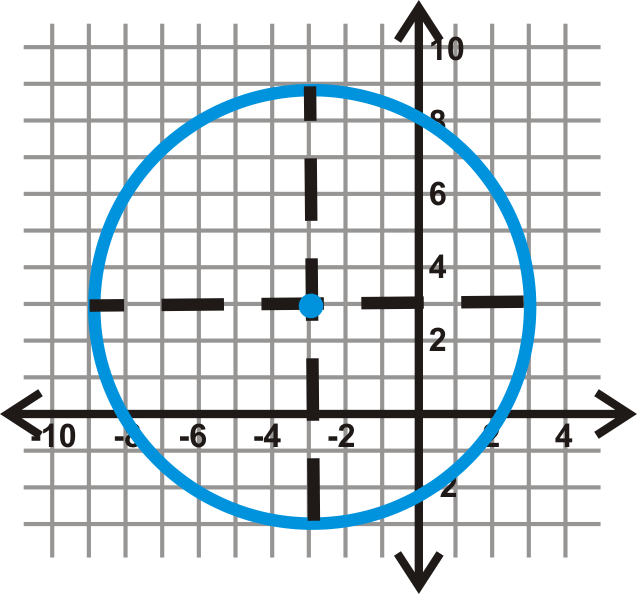
З цього ми бачимо, що центр є$(-3, 3)$. Якщо порахувати одиниці від центру до кола на будь-якому з цих діаметрів, знайдемо$r=6$. Включивши це в рівняння кола, отримуємо:$(x−(−3))^2+(y−3)^2=6^2$ або$(x+3)^2+(y−3)^2=36$.

Приклад$\PageIndex{5}$

Визначте, чи є наступні пункти$(x+1)^2+(y−5)^2=50$.

Рішення

Підключіть точки для x і y в$(x+1)^2+(y−5)^2=50$.

1. $(8, -3)$

$\begin{aligned} (8+1)^2+(−3−5)^2&=50 \\ 9^2+(−8)^2&=50 \\ 81+64 &\neq 50\end{aligned}$

$(8, -3)$не на колі

2. $(-2, -2)$

$\begin{aligned} (−2+1)^2+(−2−5)^2&=50 \\ (−1)^2+(−7)^2&=50 \\ 1+49&=50\end{aligned}$

$(-2, -2)$знаходиться на колі

Рецензія

Знайдіть центр і радіус кожного кола. Потім графуйте кожне коло.

1. $(x+5)^2+(y−3)^2=16$
2. \ (х ^ 2+ (y+8) ^2=4
3. \ (x−7) ^2+ (y−10) ^2=20
4. \ (x+2) ^2+y^2=8

Знайдіть рівняння кіл нижче.

5. 

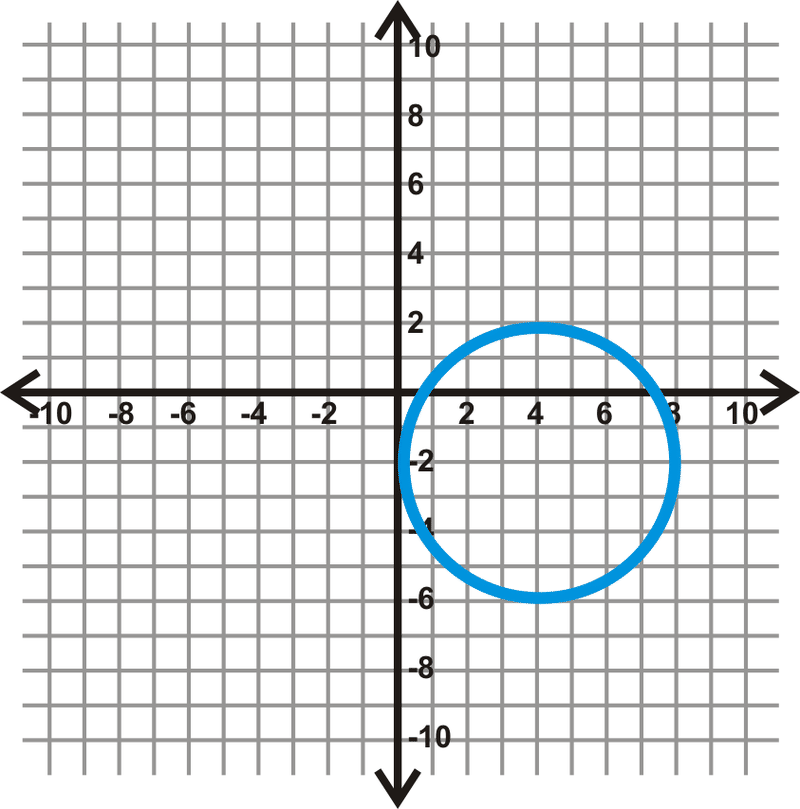
   Малюнок$\PageIndex{6}$

6. 

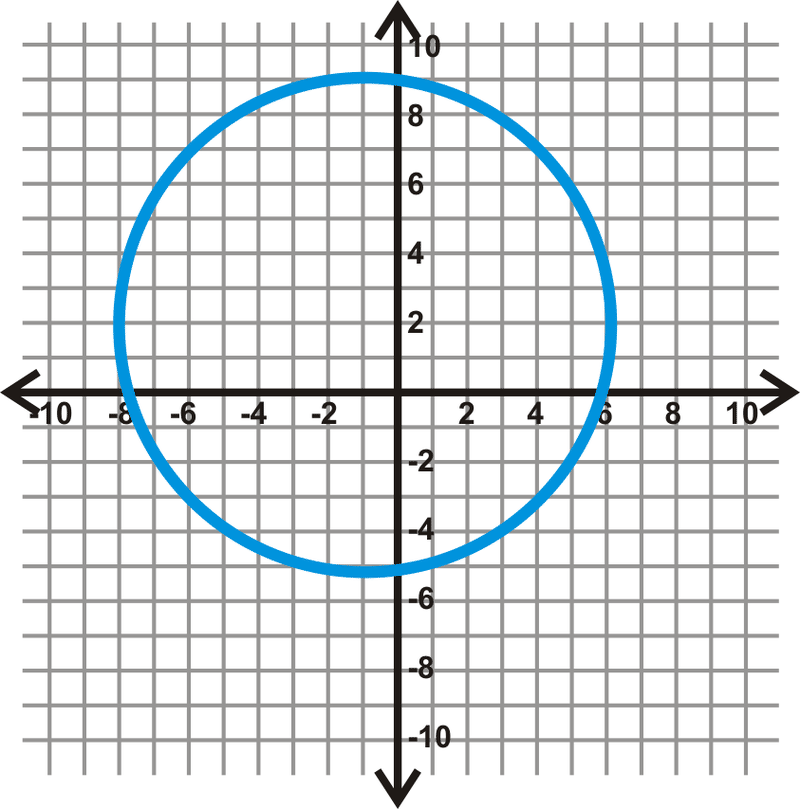
   Малюнок$\PageIndex{7}$

7. 

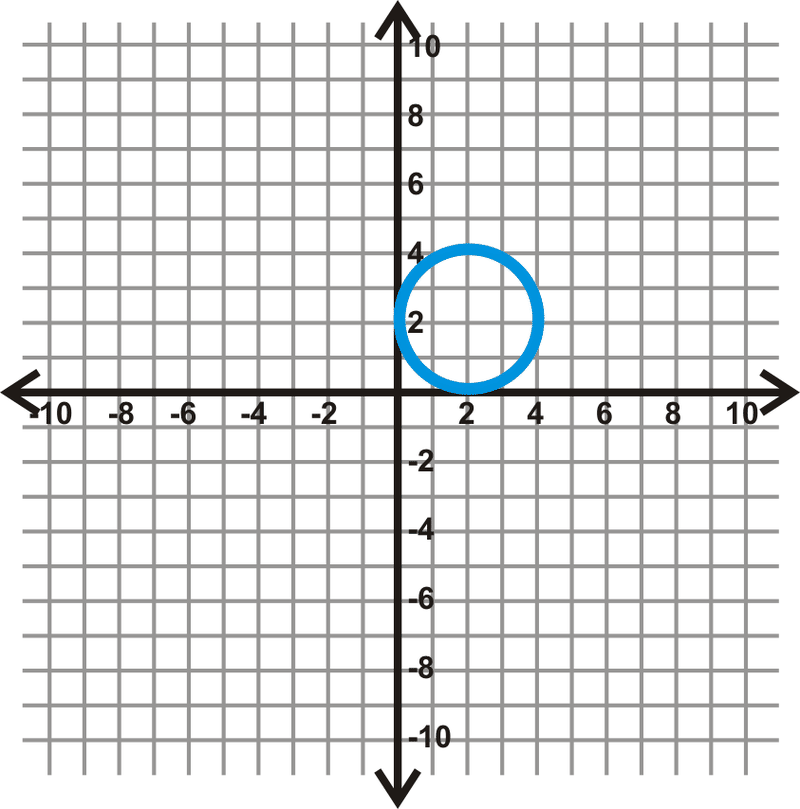
   Малюнок$\PageIndex{8}$

8. 

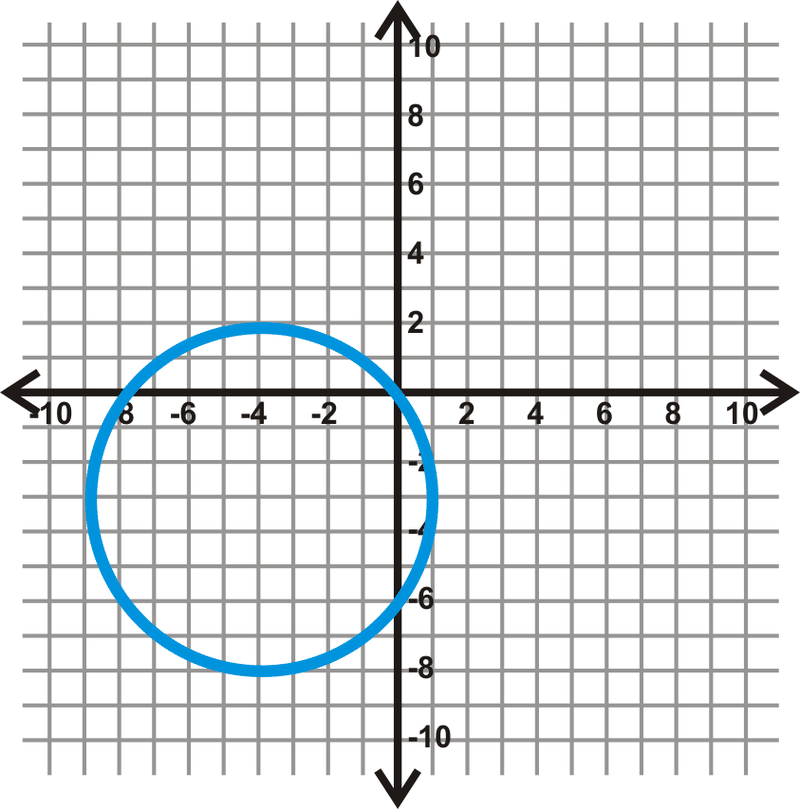
   Малюнок$\PageIndex{9}$

9. Чи є (-7, 3) на$(x+1)^2+(y−6)^2=45$?
10. Чи є (9, -1) на$(x−2)^2+(y−2)^2=60$?
11. Чи є (-4, -3) на$(x+3)^2+(y−3)^2=37$?
12. Чи є (5, -3) на$(x+1)^2+(y−6)^2=45$?

Знайдіть рівняння кола з заданим центром і точкою на колі.

13. центр: (2, 3), точка: (-4, -1)
14. центр: (10, 0), точка: (5, 2)
15. центр: (-3, 8), точка: (7, -2)
16. центр: (6, -6), точка: (-9, 4)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 9.12.

Лексика

Термін	Визначення
коло	Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
радіус	Відстань від центру до зовнішнього обідка кола.
Формула відстані	Відстань між двома точками$(x_1, y_1)$ і$(x_2, y_2)$ може бути визначено як$d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}$.
Походження	Походження - точка перетину осей x і y на декартовій площині. Координати початку координат є (0, 0).

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи графічних кіл - Основні

Види діяльності: Кола в координатній площині Дискусійні питання

Навчальні посібники: властивості кола навчальний посібник

Практика: Кола в координатній площині

Реальний світ: Геометрія GPS