Skip to main content
LibreTexts - Ukrayinska

6.18: Дотичні лінії

  1. Last updated
  2. Save as PDF
  • Page ID
    54500

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Лінії, перпендикулярні радіусу, проведені до точки дотику.

    Теореми про дотичну лінію

    Існують дві важливі теореми про дотичні лінії.

    1. Теорема дотичної до кола: Лінія є дотичною до кола тоді і тільки тоді, коли пряма перпендикулярна радіусу, проведеному до точки дотику.

    F-D_A0971 ФЧ 239 ДФФ 6Д9БА 0ЕС252436А0А84 Грудень 6826 Фабе 74ЕД1А3Ф444+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    \(\overleftrightarrow{BC}\)дотична в точці,\(B\) якщо і тільки якщо\(\overleftrightarrow{BC}\perp \overline{AB}\).

    Ця теорема використовує слова «якщо і тільки якщо», роблячи її біумовним твердженням, що означає, що зворотне значення цієї теореми також вірно.

    2. Теорема про дві тангенси: Якщо два дотичні відрізки малюються до одного кола з тієї ж зовнішньої точки, то вони конгруентні.

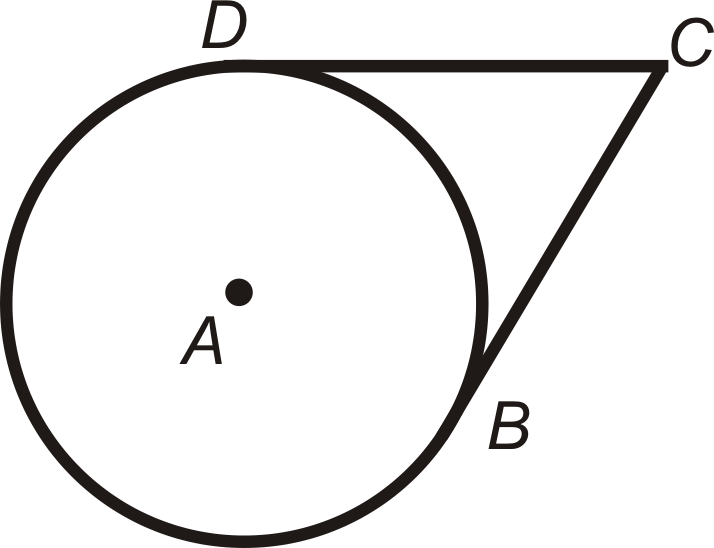
    F-D_14 ББББ 368146783Д10Ф3Д3Ф271012Б1165Е8Б2Е432Д8 АБК 8C291E944C+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    \(\overline{BC}\)і\(\overline{DC}\) мають\(C\) як кінцеву точку і є дотичними;\(\overline{BC}\cong \overline{DC}\).

    Що робити, якщо лінія була проведена поза колом, яке, здавалося, торкається кола лише в одній точці? Як ви могли визначити, чи ця лінія насправді є дотичною?

    Приклад\(\PageIndex{1}\)

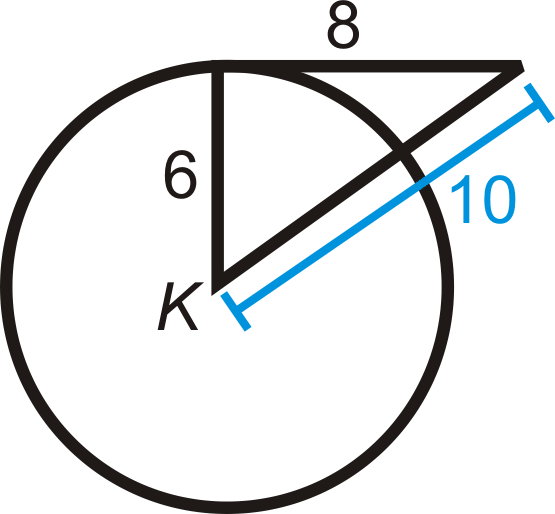
    Визначте, чи трикутник нижче є прямокутним трикутником.

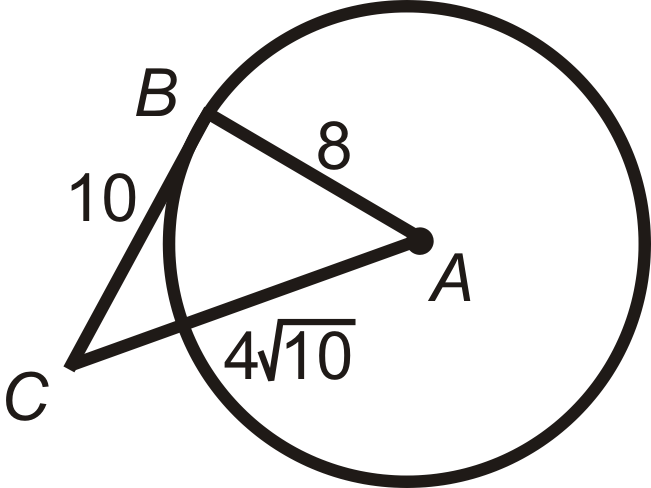
    Ф-д_СЕ2С0Б86512 ДК266С82С4АЧ5С56ЕД ФЕ31136Ф8Б9Ф 60БФ 1172893D+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Використовуйте теорему Піфагора. \(4\sqrt{10}\)є найдовшою стороною, так і буде\(c\).

    Чи

    \(\begin{aligned} 8^2+10^2&= (4\sqrt{10})^2? \\ 64+100&\neq 160\end{aligned}\)

    \(\Delta ABC\)це не прямокутний трикутник. З цього ми також знаходимо,\(\overline{CB}\) що не дотичне до\(\bigodot A\).

    Приклад\(\PageIndex{2}\)

    Якщо\(D\) і\(C\) є центрами і\(AE\) є дотичними до обох кіл, знайдіть\(DC\).

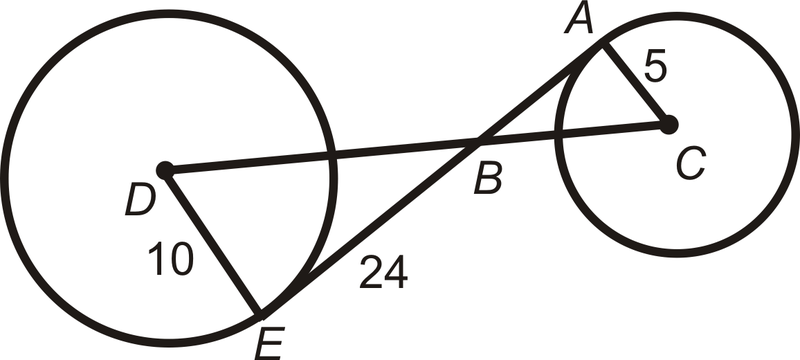
    F-D_1617D3B1028C861A04CDC 19d995E14943d47798007 Фад38E0B099A4+зображення_крихіткий+зображення_крихіткий_крошечкою.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    \(\overline{AE}\perp \overline{DE}\)і\(\overline{AE}\perp \overline{AC}\) і\(\Delta ABC \sim \Delta DBE\) по AA подібності.

    Щоб знайти\(DB\), скористайтеся теоремою Піфагора.

    \(\begin{aligned} 10^2+24^2&=DB^2 \\ 100+576&=676 \\ DB&=\sqrt{676}=26 \end{aligned}\)

    Щоб знайти\(BC\), використовуйте аналогічні трикутники.

    \(\dfrac{5}{10}=\dfrac{BC}{26}\rightarrow BC=13. \: DC=DB+BC=26+13=39\)

    Приклад\(\PageIndex{3}\)

    \(\overline{CB}\)дотична до\(\bigodot A\) точки\(B\). Знайти\(AC\). Зменшити будь-які радикали.

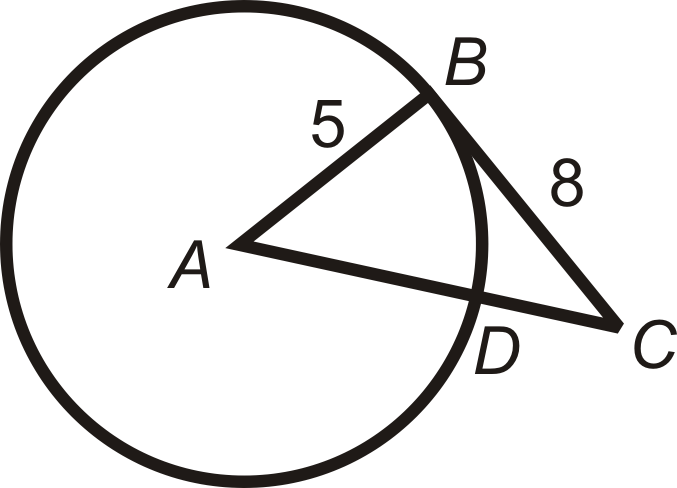
    F-D_7 ДБ605Д5Д5БА0749Е9Е138А 8 БК Д 3Б ФЕБА 5 ліжок 1А4561 ПКД 6355Е5С906+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    \(\overline{CB}\)дотична, так\(\overline{AB}\perp \overline{CB}\) і\(\Delta ABC\) прямокутний трикутник. Використовуйте теорему Піфагора, щоб знайти\(AC\).

    \(\begin{aligned} 5^2+8^2&=AC^2 \\ 25+64&=AC^2 \\ 89&=AC^2 \\ AC&=\sqrt{89}\end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Використовуючи відповідь з Прикладу А вище, знайдіть\(DC\) в\(\bigodot A\). Округлите свою відповідь до найближчої сотої.

    F-D_99633 БА 38ДБ БД 08Д7442 АБ8 ФК 5090387Б64Д0200713ЕЕ9645 БББДБ5+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    \(\begin{aligned} DC&=AC−AD \\ DC&=\sqrt{89}−5 \approx 4.43 \end{aligned}\)

    Приклад\(\PageIndex{5}\)

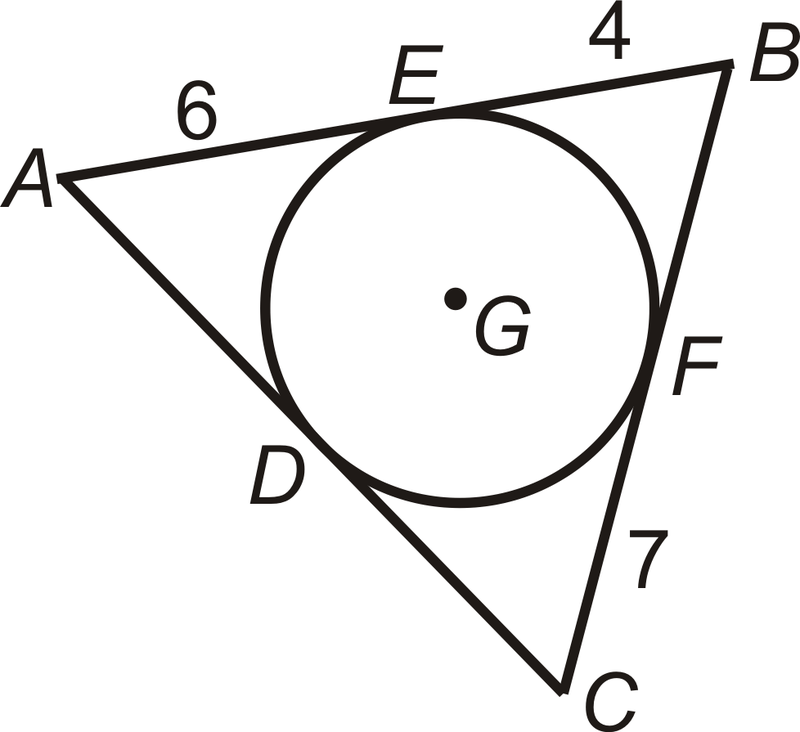
    Знайдіть периметр\(\Delta ABC\).

    F-D_57357 Абе 2ДД43ФФ 73Б3Е6Ф00306589Ф2ДК 9181 CEF73C05B80C77634+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Рішення

    \(AE=AD\),\(EB=BF\), і\(CF=CD\). Тому периметр

    \(\Delta ABC=6+6+4+4+7+7=34\).

    \(\bigodot G\)вписаний в\(\Delta ABC\). Коло вписується в багатокутник, якщо кожна сторона багатокутника дотична до кола.

    Рецензія

    Визначте, чи є даний відрізок дотичним до\(\bigodot K\).

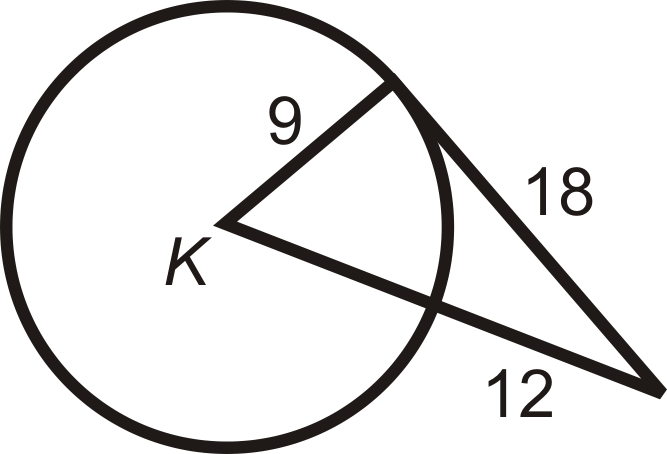
    1. F-д_0a3 ЕС2115d487E67307ЕЕД 6021 фад 427ф7253591d24cc09d06265+зображення_крихітка_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
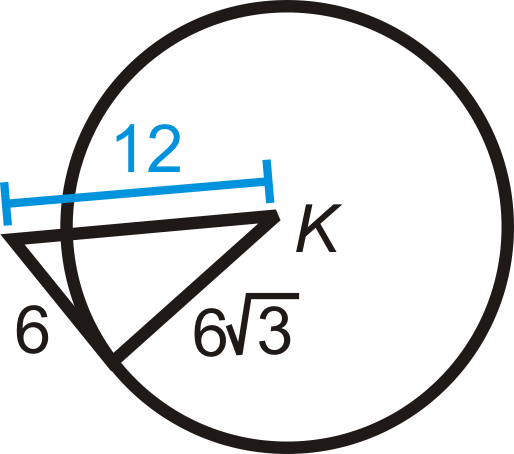
    2. F-д_ЕФК 7896 ЕБА 8Б9 ЕЕ5499113E8Ф06Е8БФ 916 де 25ФКФ Е8ДА1КС7ДФ344+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
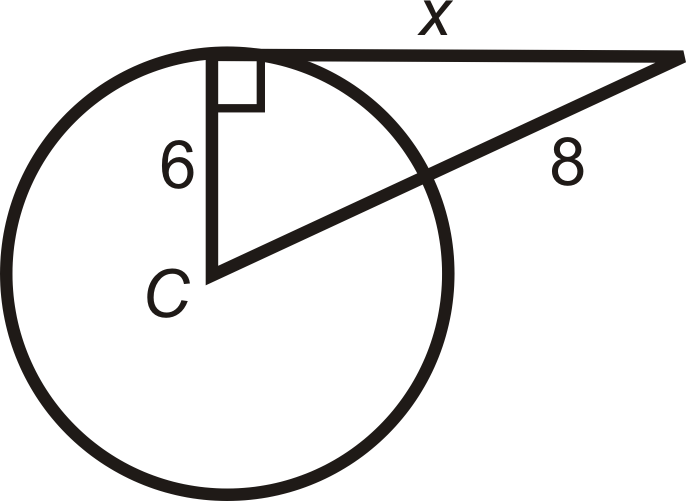
    3. Ф-д_АЕ 3338Е2Ф3Д 916678ФБФ678ФБ690Б4089Д8Е47Е419 АЕФ46114ЦЕЕЕ11011Ф+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)

    Знайти значення зазначеної довжини (s) в\(\bigodot C\). \(A\)і\(B\) є точками дотику. Спрощення всіх радикалів.

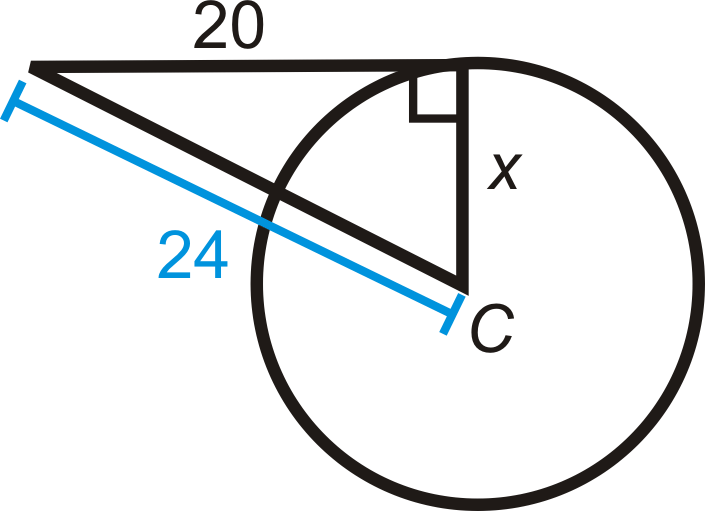
    1. Ф-Д_46Ф5Б 661 БА 76992125Ф859А83710С2Б763Ф83559 ДДФФ 1ДФББ394+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
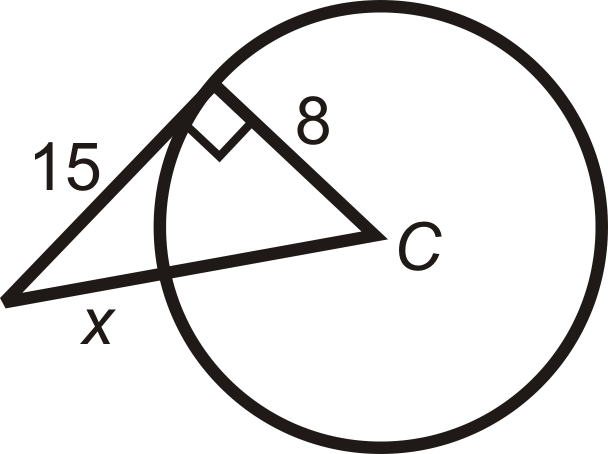
    2. Ф-Д_КС 87Б8981383дек 8 FE40154C5384523Е 38878 Ф2ФБ3А6Ф3А6Д 45Ф2+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
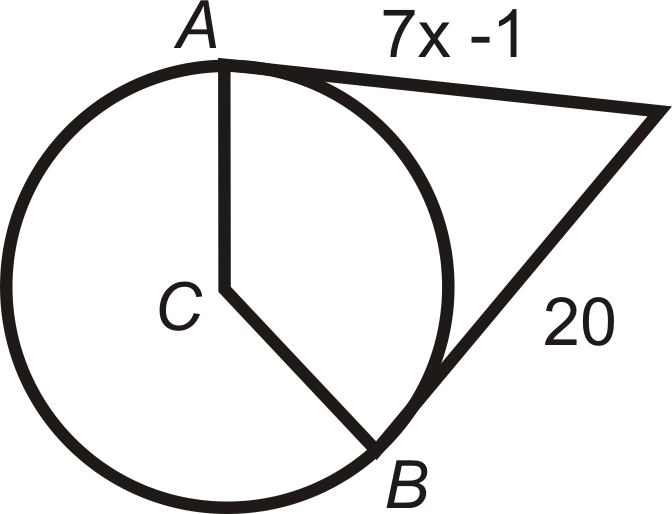
    3. F-д_93 ФА2Б56С4Д4Е6Б3А4600489 БК 52А9С67С87Е1ААЕ48Д40Б18801Ф52+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
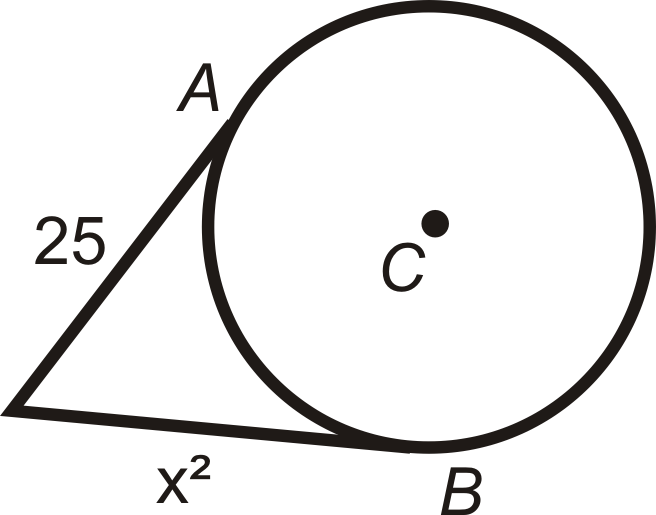
    4. F-D_C21EB973AF 57 ААС 906Ф217 Фе 83793БД Д 094Ф3БДБ0Д8690Б3ЕЦ0Б3ЕС0С+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
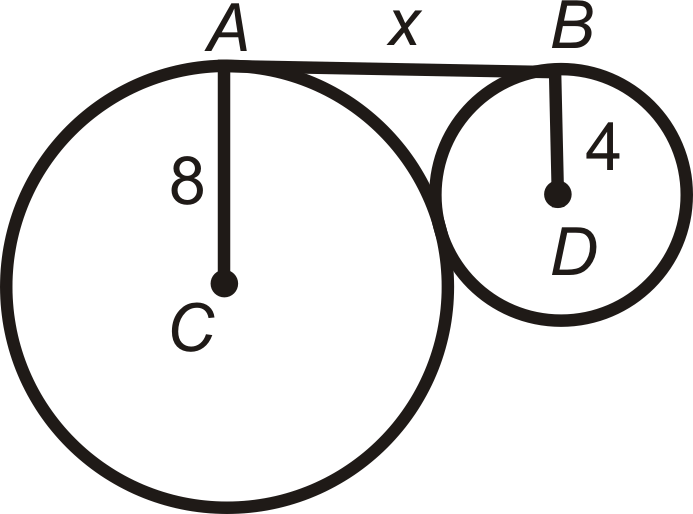
    5. F-D_2A842B2FDC 3Б4Е96Д97Ф1СБ945А1С7Д8Б1А16А07Е9419ЕБ76Д68Б+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
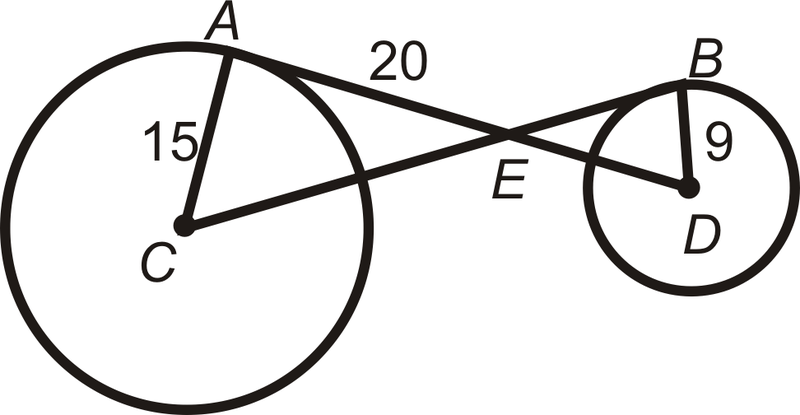
    6. F-д_47д14ф 7070д 46874АА6Е 3008Б7Е9507D3AE7C9E5246A81 DeF3484F9+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)

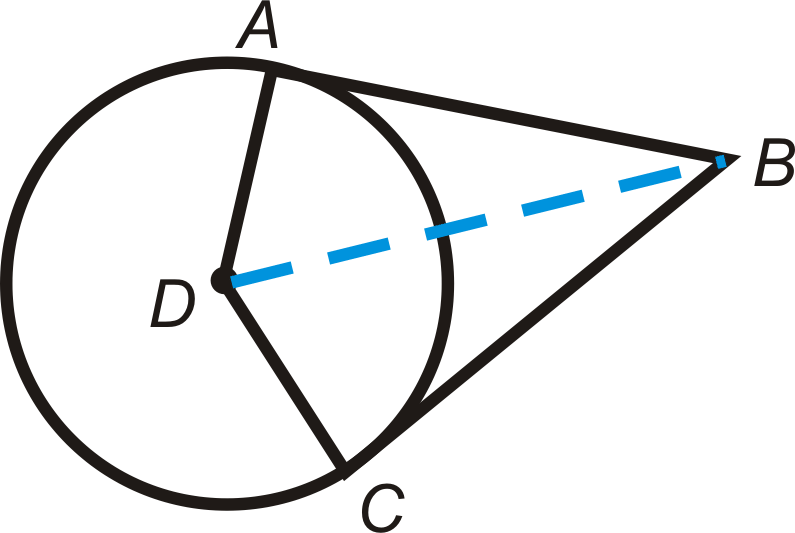
    \(A\)і\(B\) є точками дотику для\(\bigodot C\) і\(\bigodot D\).

    Ф-д_8е79ФБ92С98Д8А0Е 039782СА211671 БК 23СС0Д7Е4А2СА5082Е648А9+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{17}\)
    1. Є\(\Delta AEC \sim \Delta BED\)? Чому?
    2. Знайти\(CE\).
    3. Знайти\(BE\).
    4. Знайти\(ED\).
    5. Знайти\(BC\) і\(AD\).

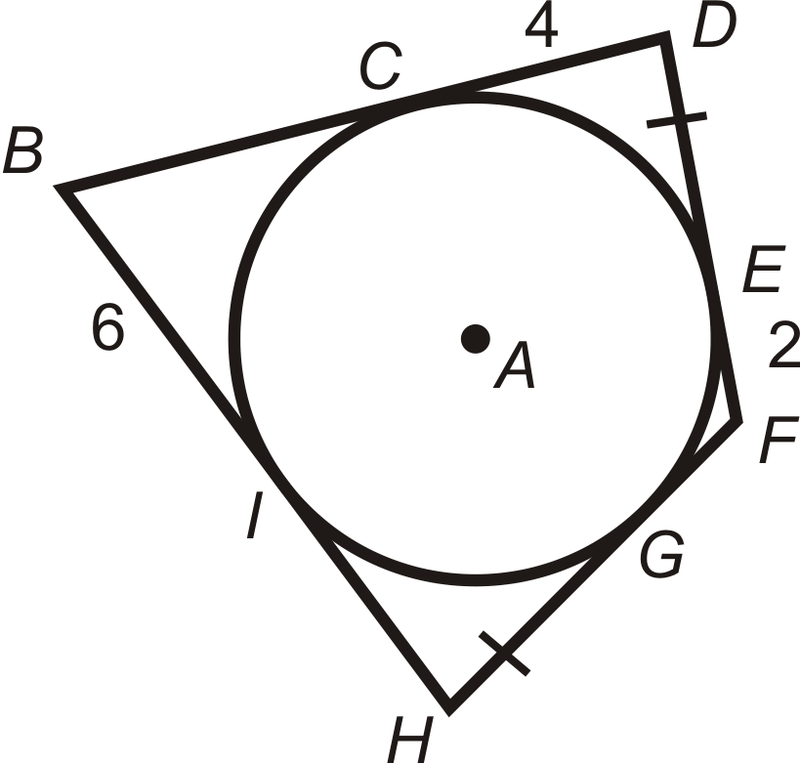
    \(\bigodot A\)вписаний в\(BDFH\).

    F-D_A5 А5ДА 34Д86ЕФ34ББ8ЕД ФА9С48 АЕС1Ф4 ББ5Е3С166Ф912Е1БД96БКК89+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{18}\)
    1. Знайдіть периметр\(BDFH\).
    2. Який тип чотирикутника буває\(BDFH\)? Звідки ти знаєш?
    3. Намалюйте коло, вписаний в квадрат. Якщо радіус кола дорівнює 5, який периметр квадрата?
    4. Чи можна вписати коло в прямокутник? Якщо так, намалюйте його. Якщо ні, поясніть.
    5. Намалюйте трикутник з двома сторонами, дотичними до кола, але третю сторону немає.
    6. Чи можна вписати коло в тупий трикутник? Якщо так, намалюйте його. Якщо ні, поясніть.
    7. Заповніть пробіли в доказі теореми про дві тангенси.

    Дано:\(\overline{AB}\) і\(\overline{CB}\) з точками дотику в\(A\) і\(C\). \(\overline{AD}\)і\(\overline{DC}\) є радіусами.

    Доведіть:\(\overline{AB}\cong \overline{CB}\)

    Заява Причина
    1. 1.
    2. \(\overline{AD}\cong \overline{DC}\) 2.
    3. \(\overline{DA}\perp \overline{AB}\)і\(\overline{DC}\perp \overline{CB}\) 3.
    4. 4. Визначення перпендикулярних ліній
    5. 5. Підключення двох існуючих точок
    6. \(\Delta ADB\)і\(\Delta DCB\) є прямими трикутниками 6.
    7. \(\overline{DB}\cong\overline{DB}\) 7.
    8. \(\Delta ABD\cong \Delta CBD\) 8.
    9. \(\overline{AB}\cong \overline{CB}\) 9.
    1. Заповніть пропуски, скориставшись доказом від #21.
      1. \(ABCD\)є _____________ (тип чотирикутника).
      2. Лінія, яка з'єднує ___________ і зовнішню точку\(B\) __________\(\angle ABC\).
    2. Точки\(A\)\(B\), і\(C\) є точками дотику для трьох дотичних кіл. Поясніть, чому\(\overline{AT}\cong \overline{BT}\cong \overline{CT}\).
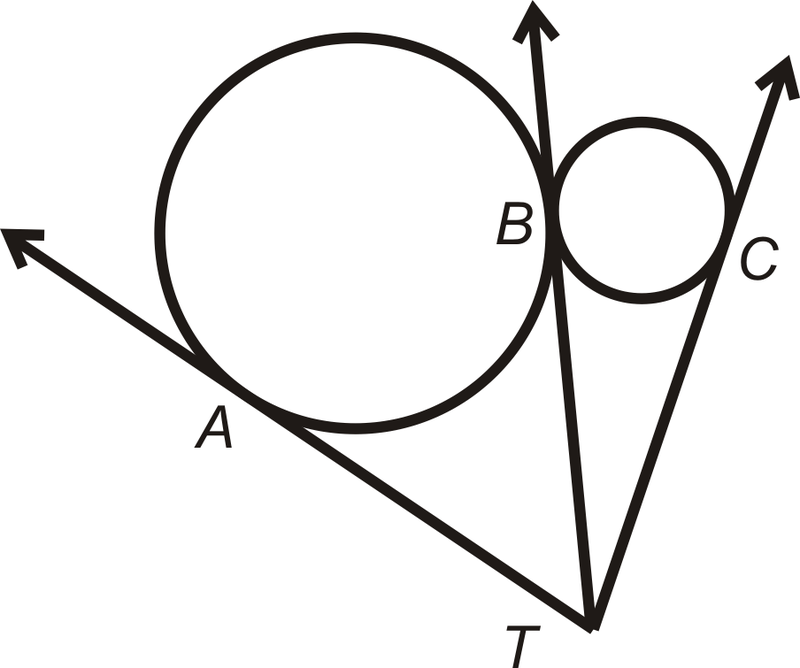
      Ф-Д_08202БА 89449389А707Б52576Ф4541Б9637БК9ДД7СА9БК43Ф019А1+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 9.2.

    Ресурси

    Лексика

    Термін Визначення
    коло Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    точка дотику Точка, де дотична лінія стосується кола.
    радіус Відстань від центру до зовнішнього обідка кола.
    Тангенс Тангенс кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, протилежної заданому куту, на довжину сторони, прилеглої до заданого кута.
    Теорема дотичної до кола Лінія є дотичною до кола тоді і тільки тоді, коли пряма перпендикулярна радіусу, проведеному до точки дотику.
    Теорема про дві тангенси Теорема про дві тангенси стверджує, що якщо два дотичні відрізки малюються до одного кола з тієї ж зовнішньої точки, то вони є конгруентними.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи дотичних ліній - основні

    Діяльність: Запитання обговорення дотичних ліній

    Навчальні посібники: властивості кола навчальний посібник

    Практика: Дотичні лінії

    Реальний світ: Гойдалки