Skip to main content
LibreTexts - Ukrayinska

6.17: Кути поза колом

  1. Last updated
  2. Save as PDF
  • Page ID
    54504

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Кути, утворені дотичними і/або секантами.

    Кут знаходиться за межами кола, якщо його вершина знаходиться за межами кола, а його сторони є дотичними або секантами. Можливості такі: кут, утворений двома дотичними, кут, утворений дотичною і січною, і кут, утворений двома секантами.

    Теорема зовнішнього кута: Міра кута, утвореного двома секантами, двома дотичними або січною та дотичною від точки поза колом, є половиною різниці мір перехоплених дуг.

    Ф-Д_ДК 68Б26Д59АЕД 9Д2Б06Б2108488 КБ8А0470А7Е8Д9437 Б3503D+зображення_крихіткий+зображення_крихіткий_крошечкий.PNG
    Малюнок\(\PageIndex{1}\)

    \(m\angle D=\dfrac{m\widehat{EF}−m\widehat{GH}}{2}\),\(m\angle L=\dfrac{m\widehat{MPN}−m\widehat{MN}}{2}\),\(m\angle Q=\dfrac{m\widehat{RS}−m\widehat{RT}}{2}\)

    Що робити, якщо вам дали коло з двома секантами, двома дотичними, або по одній з них, які мають спільну точку поза колом? Як ви можете використовувати міру дуг, утворених цими частинами кола, щоб знайти міру кута, який вони роблять поза колом?

    Приклад\(\PageIndex{1}\)

    Знайдіть міру\(x\).

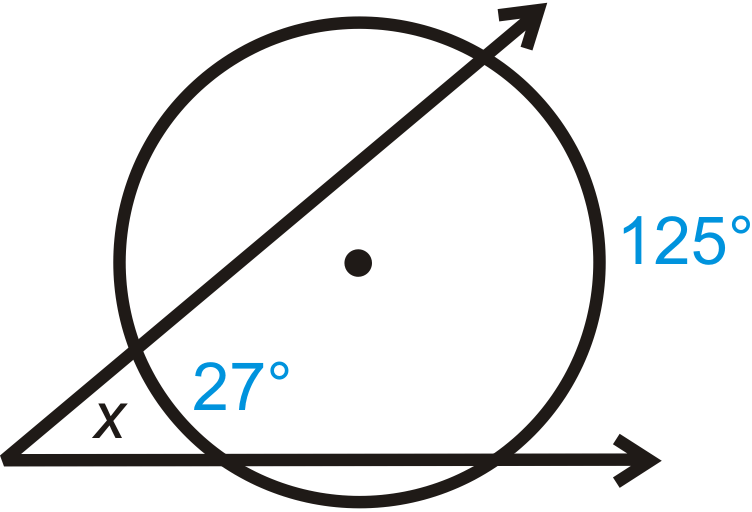
    F-д_ЕФ74ЕФ004Д0Е5715Б1 А59776 ДД836Ф3Е4А72А35270А83031А232+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Використовуйте теорему про зовнішній кут.

    \(x=\dfrac{125^{\circ} −27^{\circ}}{2}=\dfrac{98^{\circ}}{2}=49^{\circ}\)

    Приклад\(\PageIndex{2}\)

    Знайдіть міру\(x\).

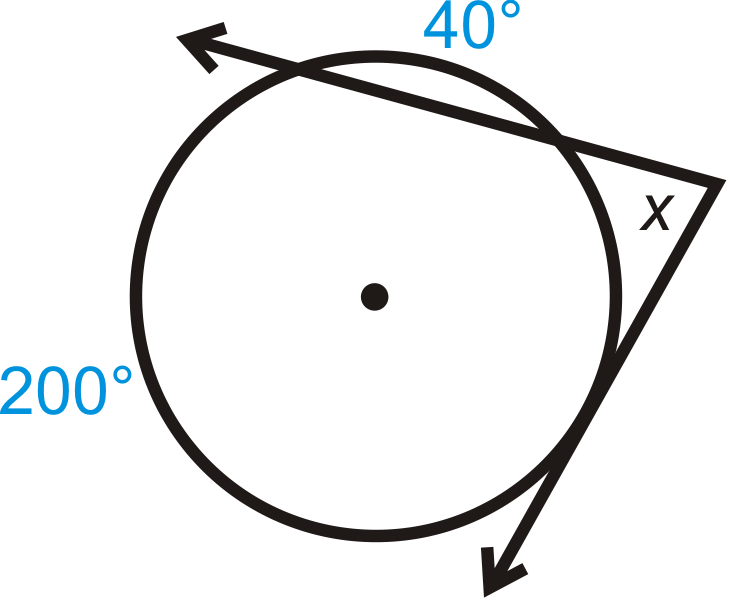
    F-D_D910АЕ 948 ФА7 А80862Д5С4А7 БАЕ35204 Е456457871Ф68052Б5А41Б+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Використовуйте теорему про зовнішній кут.

    \(40^{\circ}\)це не перехоплена дуга. Перехоплена дуга - це\(120^{\circ}\),\((360^{\circ} −200^{\circ} −40^{\circ})\). \(x=\dfrac{200^{\circ} −120^{\circ} }{2}=\dfrac{80^{\circ} }{2}=40^{\circ}\)

    Приклад\(\PageIndex{3}\)

    Знайдіть значення\(x\).

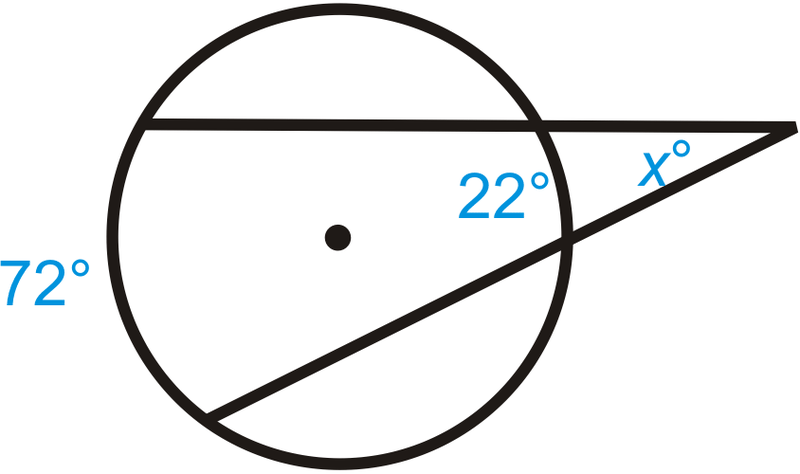
    F-D_1863C92A65103991377F12167C3E08119787C9BA77DBE368D0A+зображення_крихіткий+зображення_крихітковий_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    \(x=\dfrac{72^{\circ} −22^{\circ} }{2}=\dfrac{50^{\circ} }{2}=25^{\circ}\).

    Приклад\(\PageIndex{4}\)

    Знайдіть значення\(x\).

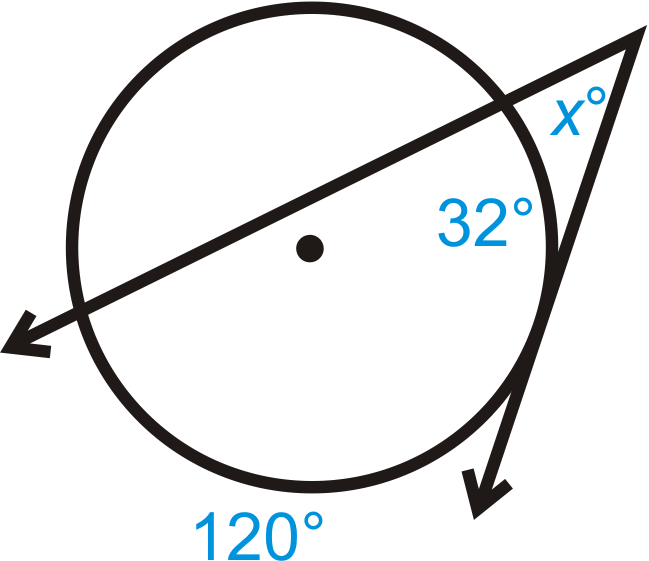
    Ф-Д_Б8 ФД7 КФ4 КС1483Е43Б1С055717Б8Д1СБЕ01ФА58ААБ50С3Ф3 EACE2E0+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    \(x=\dfrac{120^{\circ} −32^{\circ}}{2}=\dfrac{88^{\circ} }{2}=44^{\circ}\).

    Приклад\(\PageIndex{5}\)

    Знайдіть значення\(x\).

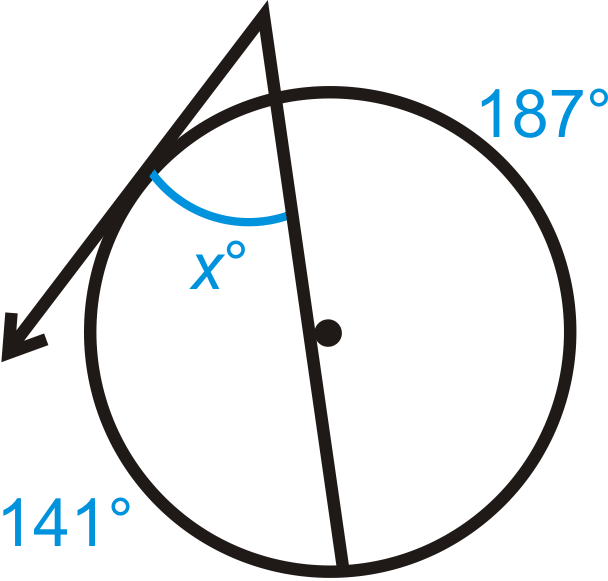
    F-д_С0ЕД 93Б22А2Б3Д 1049289Б3Е010Ф3Е72А124Б8903231d529c84F5E0+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Спочатку зауважте, що відсутня дуга за кутом\(x\) вимірює,\(32^{\circ}\) тому що повне коло повинен зробити\(360^{\circ}\). Потім,\(x=\dfrac{141^{\circ} −32^{\circ}}{2}=\dfrac{109^{\circ}}{2}=54.5^{\circ}\).

    Рецензія

    Знайти значення відсутньої змінної (ів).

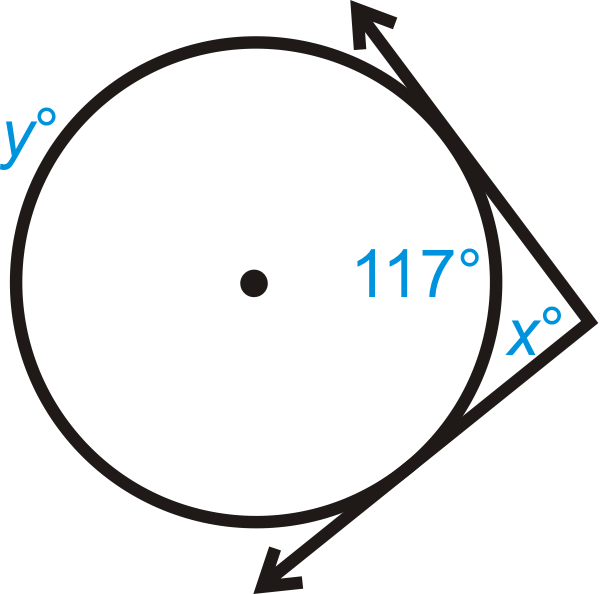
    1. F-D_7E 990Ф528Б7Д69КСА93А 37кД5 СД03Е5Д730С92497595056Б5986А280 +зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
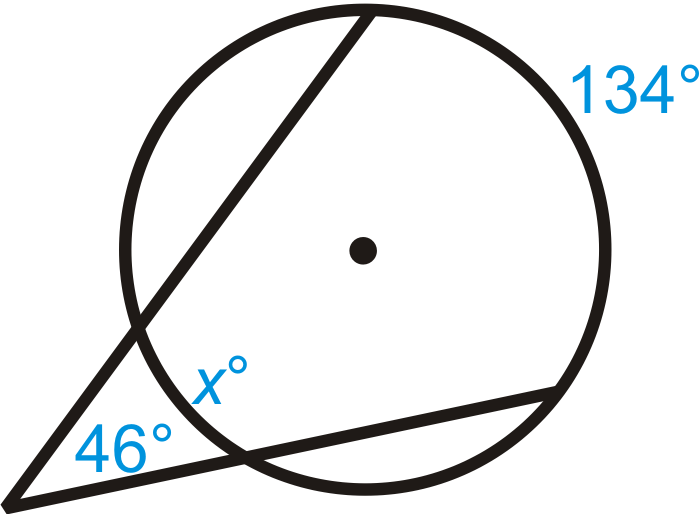
    2. F-д_дас 0029Ф 39840159996C1F303CEF130Е5 Дед 06Е21Е06АБ71054A02+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
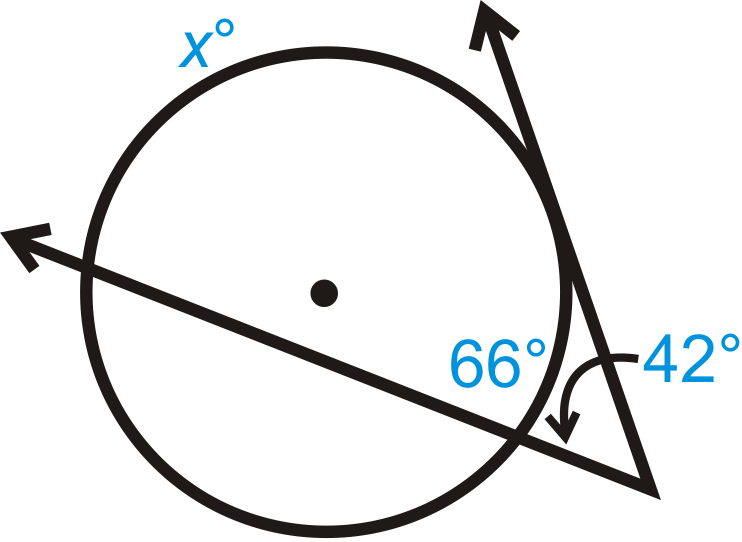
    3. F-д_9980Б767С51Б3966С1А65С48338Д5ЕА 8ФА85С5311Б21Б3С29Б96+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
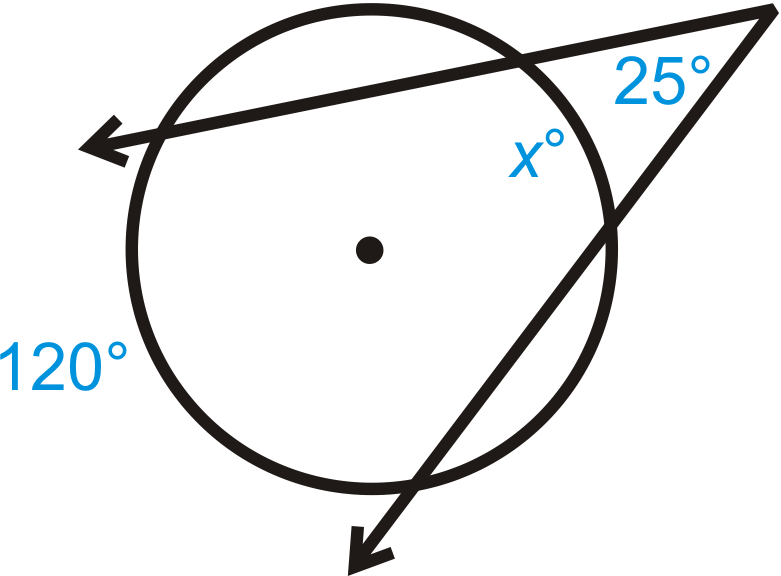
    4. F-д_699Д5Е9Е739Ф29Д 83604Б80С 24БДБ5Д5 CF20760Б951ЕД 73+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
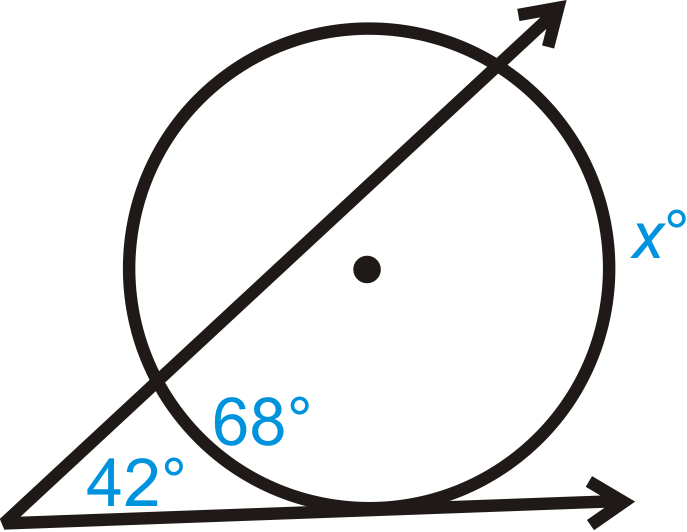
    5. F-D_0 ЕДС2Д6716ФБББ 2746Е974Е455 Е455ЕЕ99ДФ 150420C0BA718 ДБ1d886FF20+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
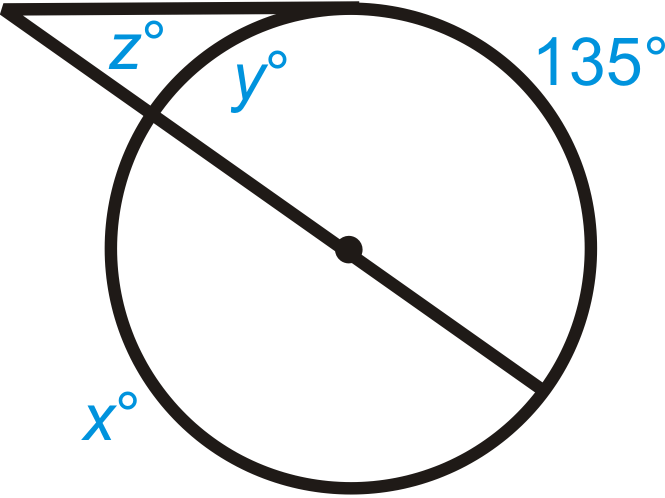
    6. F-д_23Ф 4752Б3С7ДАА2Б66538Д2Б9242881331Е158ЕФ 1784С0407506Б0А+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
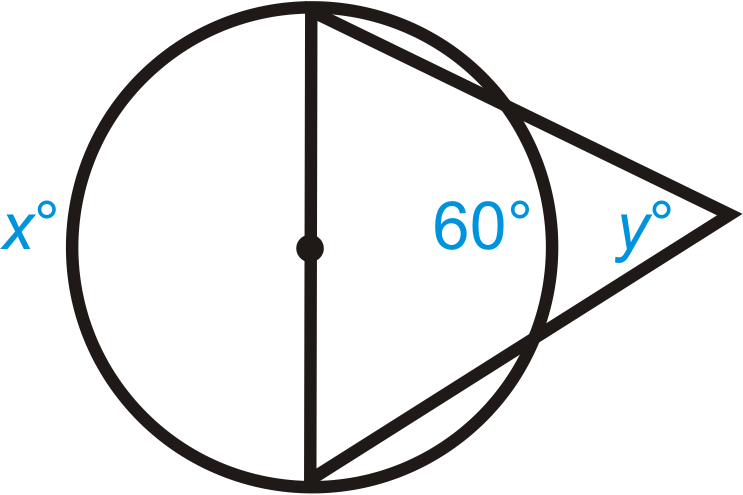
    7. Ф-Д_960Д 38Д70Ф6058ЕК CFB689B690C5BFA3Ф9Ф9Ф9Ф9Ф19Б35CF04D876FC72FC72FC+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)

    Вирішити для\(x\).

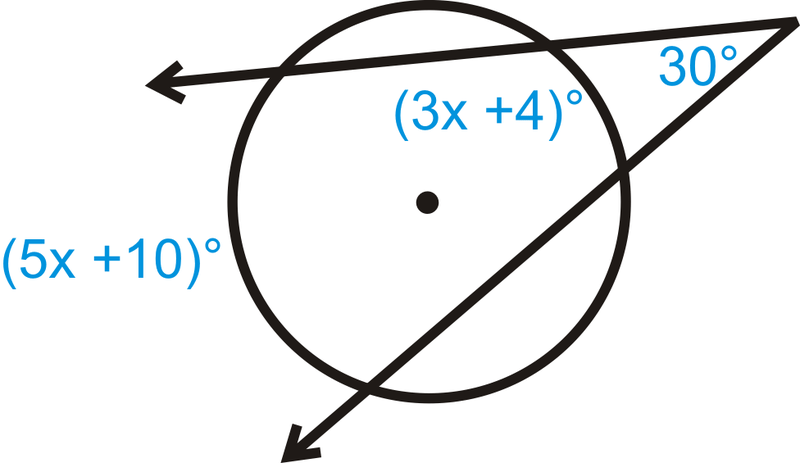
    1. Ф-д_788430Д8Ф33Ф6989А1Д2БД 08Да608937Ф9Д83Б29 ЕАА3ФЕБА 92С7413+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
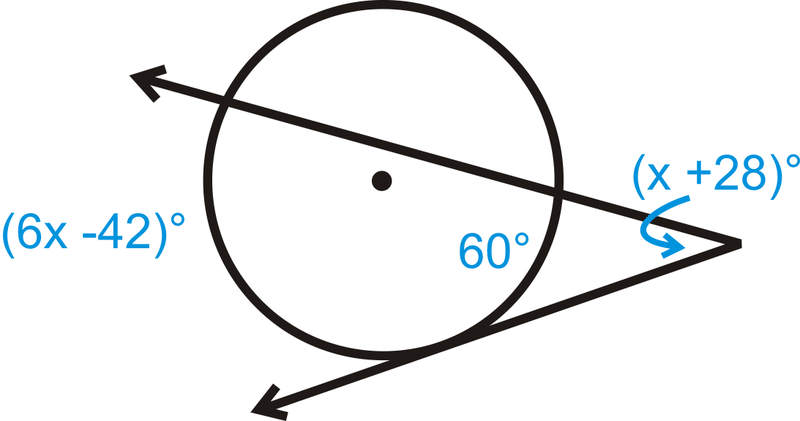
    2. Ф-д_60493252ФБ935С8Ф24206 Додати 0Е58ЕД 326Ф0БФ710Е0 ББФ 86 BBF579B4+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
    3. Заповніть пробіли доказу для теореми зовнішнього кута
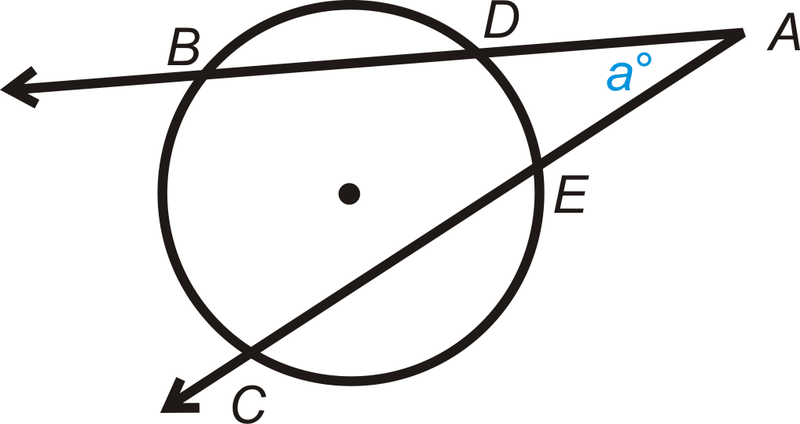
    Ф-Д_4Ф27А4ФС 6БК 357Ф53БД 119КД62БК 2346де5С968Ф04АБ 199Д05Д2С8+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{16}\)

    Дано: Січні промені\(\overrightarrow{AB}\) і\(\overrightarrow{AC}\)

    Доведіть:\(m\angle a=12(m\widehat{BC}−m\widehat{DE})\)

    Заява Причина
    1. Перетинаються секанти\(\overrightarrow{AB}\) і\(\overrightarrow{AC}\). 1.

    2. Малювати\(\overline{BE}\).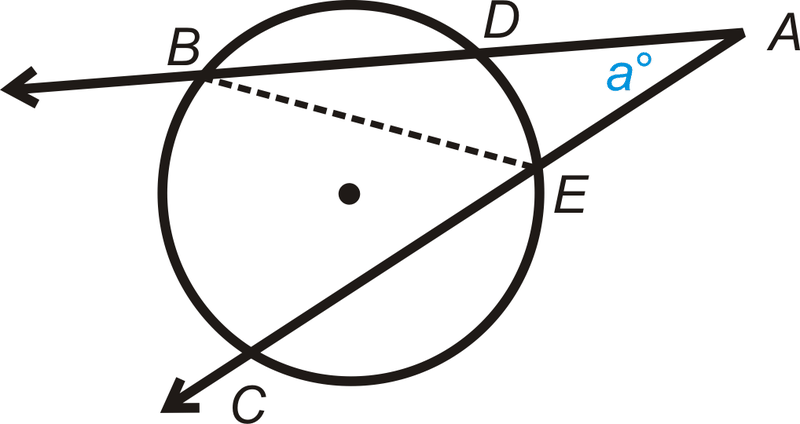

    F-D_ЕДЕ 37А 85 АББ 749 С71С2А065БК 3ФФА5989Д3Ф09С3С82ЕБФД5294380+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{17}\)
    		 2. Будівництво

    3. \(m\angle BEC=\dfrac{1}{2}m\widehat{BC}\)

    \(m\angle DBE=\dfrac{1}{2}m\widehat{DE}\)

    		 3.
    4. \(m\angle a+m\angle DBE=m\angle BEC\) 4.
    5. 5. Віднімання PoE
    6. 6. Заміна
    7. \(m\angle a=\dfrac{1}{2}(m\widehat{BC}−m\widehat{DE})\) 7.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 9.8.

    Лексика

    Термін Визначення
    центральний кут Кут, утворений двома радіусами і вершина якого знаходиться в центрі кола.
    акорд Відрізок лінії, кінцеві точки якого знаходяться на колі.
    коло Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    вписаний кут Кут з його вершиною на колі і сторони якого є хордами.
    перехоплена дуга Дуга, яка знаходиться всередині вписаного кута і кінцеві точки якої знаходяться на куті.
    точка дотику Точка, де дотична лінія стосується кола.
    радіус Відстань від центру до зовнішнього обідка кола.
    Секантний Секанс кута в прямокутному трикутнику - це величина, знайдена діленням довжини гіпотенузи на довжину сторони, прилеглої до заданого кута. Відношення секанс - це зворотне косинусного відношення.
    Тангенс Тангенс кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, протилежної заданому куту, на довжину сторони, прилеглої до даного кута.
    Теорема про зовнішні кути Теорема про зовнішні кути стверджує, що міра кута, утвореного двома секантами, двома тангенсами або секансом і дотичною від точки поза колом, є половиною різниці мір перехоплених дуг.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи кутів поза колом - основні

    Види діяльності: Кути поза колом Дискусійні питання

    Навчальні посібники: Дуги та кути Навчальний посібник

    Практика: Кути поза колом