Skip to main content
LibreTexts - Ukrayinska

6.15: Вписані чотирикутники в колах

  1. Last updated
  2. Save as PDF
  • Page ID
    54483

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Чотирикутники з кожною вершиною на колі та протилежними кутами, які є додатковими.

    Вписаний багатокутник - це багатокутник, де кожна вершина знаходиться на колі, як показано нижче.

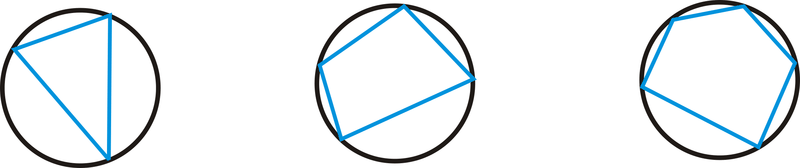
    F-D_3B423CE4D07F83ФК 74Ф35д7 ЕЦК 4Б7Б0Ф212 Ф6Е 6E6236319FDE1D+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Зокрема, для вписаних чотирикутників протилежні кути завжди будуть додатковими.

    Вписана теорема чотирикутника: Чотирикутник може бути вписаний в коло тоді і лише тоді, коли протилежні кути є додатковими.

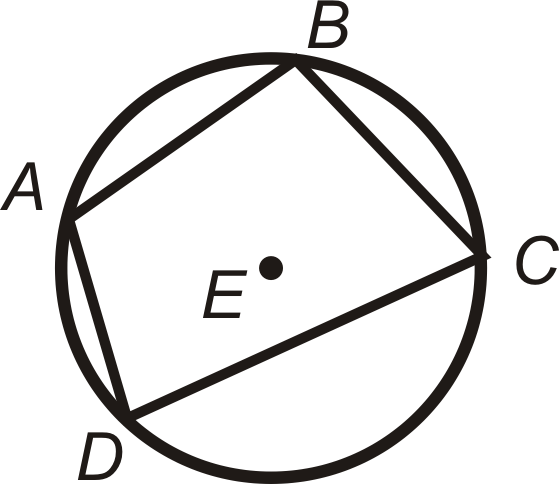
    F-D_234 АЕД 0С25АБ 3088 ЕЕ1539Ф4Ф8КБД Д 779 КБД 55821268 CF106C165F1+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Якщо\(ABCD\) вписаний в\(\bigodot E\), то\(m\angle A+m\angle C=180^{\circ}\) і\(m\angle B+m\angle D=180^{\circ}\). І навпаки, якщо\(m\angle A+m\angle C=180^{\circ}\) і\(m\angle B+m\angle D=180^{\circ}\),\(ABCD\) то вписаний в\(\bigodot E\).

    Що робити, якщо вам дали коло з вписаним в нього чотирикутником? Як ви могли використовувати інформацію про дуги, утворені чотирикутником та/або кутовими мірами чотирикутника, щоб знайти міру невідомих чотирикутників?

    Приклад\(\PageIndex{1}\)

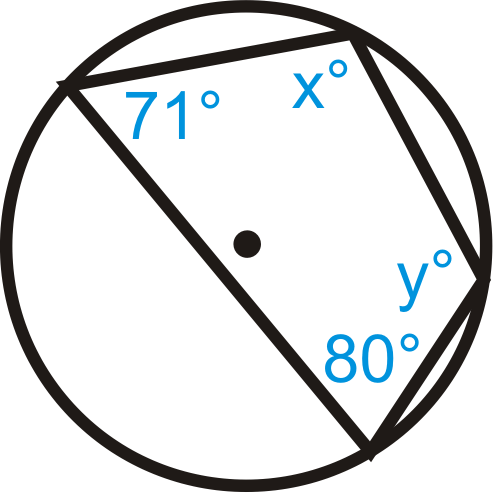
    1. F-D_F24B37126D5836 ФД55ДБ753ЕЕБ 521107C3754F643667625 Дакаф 1479+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{3}\)
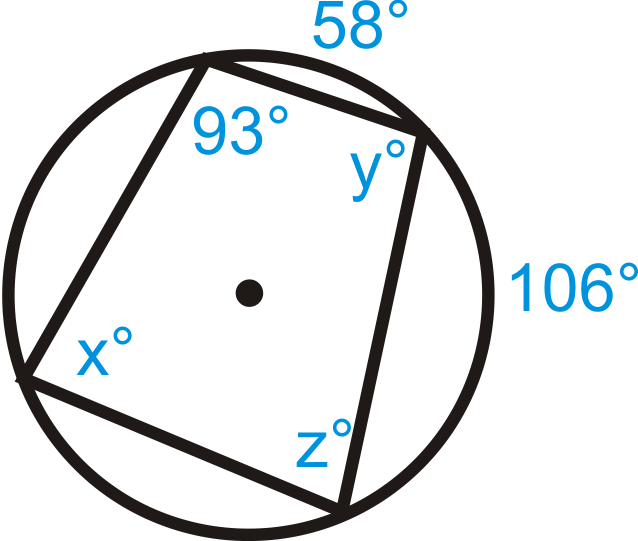
    2. F-D_4E9 FA23995200FF2BCE5845А55АА0Б9А3 подача Б20776807DA7788843C+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{4}\)

    Рішення

    1. \ (\ почати {вирівняний}
      x+80^ {\ circ} &=180^ {\ circ}\ qquad& y+71^ {\ circ} &=180^ {\ circ}\\
      x&=100^ {\ circ} & y&=109^ {\ circ}
      \ кінець {вирівняний}\)
    1. \ (\ почати {вирівняний}
      z+93^ {\ circ} &=180^ {\ circ} & x =\ розриву {1} {2}\ ліворуч (58^ {\ circ} +106^ {\ circ}\ праворуч) & y+82^ {\ circ} &= 180^ {\ circ}\
      z &=87^ {\ circ} & x =82^ {\ circ} & y&=98^ {\ circ}
      \ кінець {вирівняний}\)

    Приклад\(\PageIndex{2}\)

    Знайти\(x\) і\(y\) на зображенні нижче.

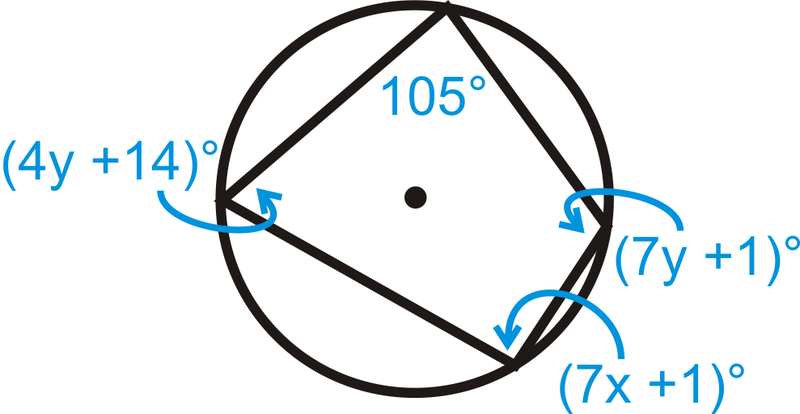
    F-Д_64Ф8Д45Д7БД Д 8Е76А6Д0С885 ЕКА 321Е6148062 FeA389C6837FF75D+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    \ (\ почати {масив} {rlrl}
    (7 х+1) ^ {\ цирк} +105^ {\ цирк} & =180^ {\ цирк} & (4 y+14) ^ {\ circ} + (7 y+1) ^ {\ circ} & =180^ {\ цирк}\\
    7 x+106^ {\ circ} & =180^ {\ цирк} & 11 y+15^ {\ коло} & =180^ {\ коло}\\
    7 х & = 74 & 11 y & =165\\
    x & ; =10.57 & y&=15
    \ кінець {масив}\)

    Приклад\(\PageIndex{3}\)

    Знайти значення x і y в\(\bigodot A\).

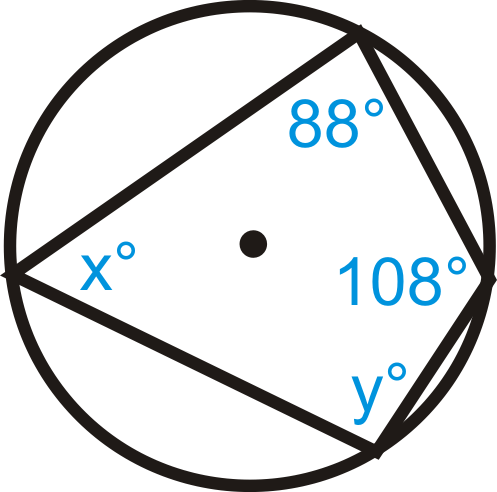
    F-д_Ф2А 4ФБ83ЕС82Д7580БД9Е11 ЕФБ85Д1 дефафад 3Б1188С5С7Ф5ЕС3+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Використовуйте теорему про вписаний чотирикутник. \(x^{\circ}+108^{\circ}=180^{\circ}\)так\(x=72^{\circ}\). Аналогічно\(y^{\circ}+88^{\circ}=180^{\circ}\) так\(y=92^{\circ}\).

    Приклад\(\PageIndex{4}\)

    \(ABCD\)Чотирикутник вписаний в\(\bigodot E\). Знайти\(m\angle A\),\(m\angle B\),\(m\angle C\), і\(m\angle D\).


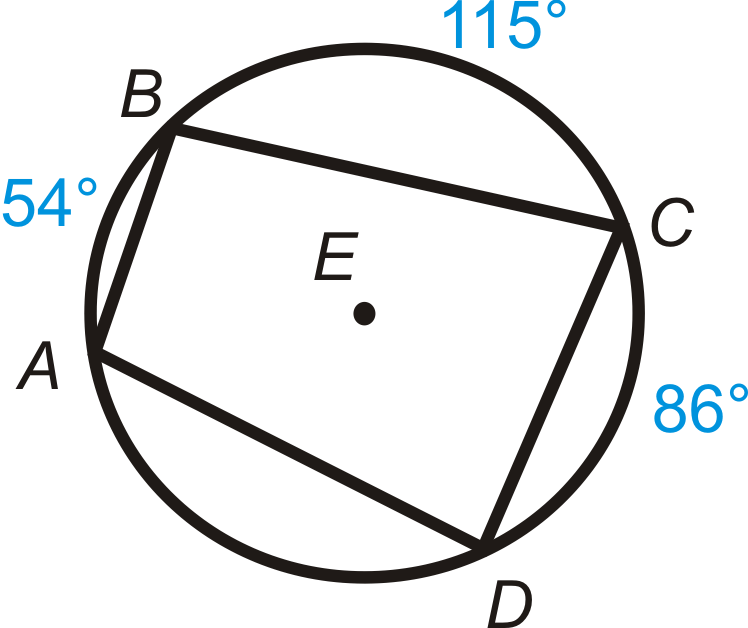
    F-д_28916d1f401e34988707414 ADB44C915487A4А4Ф08050767BFFF944C90+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Рішення

    По-перше, зверніть увагу, що\(m\widehat{AD}=105^{\circ}\) тому, що повне коло повинен складатися до\(360^{\circ}\).

    \(\begin{aligned}m\angle A&=\dfrac{1}{2}m\widehat{BD}=12(115+86)=100.5^{\circ} \\ m\angle B&=\dfrac{1}{2}m\widehat{AC}=12(86+105)=95.5^{\circ} \\ m\angle C&=180^{\circ}−m\angle A=180^{\circ}−100.5^{\circ}=79.5^{\circ} \\ m\angle D&=180^{\circ}−m\angle B=180^{\circ}−95.5^{\circ}=84.5^{\circ}\end{aligned}\)

    Рецензія

    Заповніть заготовки.

    1. A (n) _______________ багатокутник має всі свої вершини на колі.
    2. _____________ кути вписаного чотирикутника - ________________.

    \(ABCD\)Чотирикутник вписаний в\(\bigodot E\). Знайти:

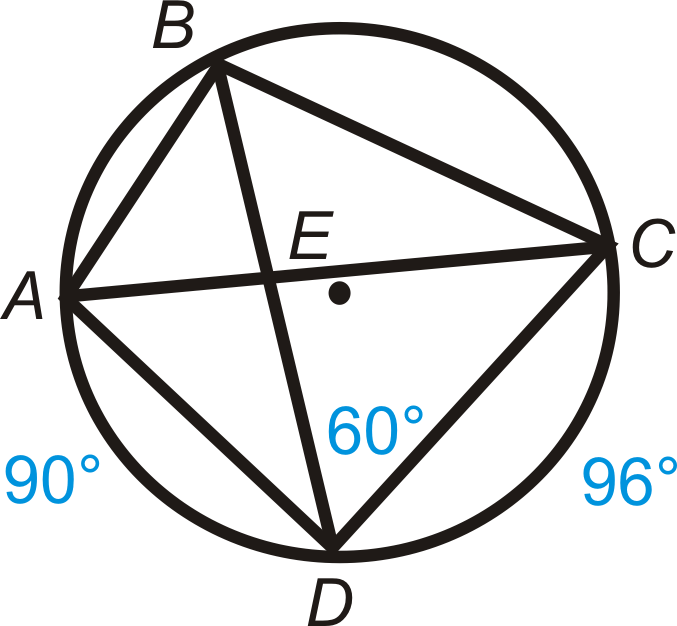
    F-D_3ББ0Б500960D9ФБД9502ДБФ 49АБ2Б3Б335Д5ББК4228E01F369+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)
    1. \(m\angle DBC\)
    2. \(m\widehat{BC}\)
    3. \(m\widehat{AB}\)
    4. \(m\angle ACD\)
    5. \(m\angle ADC\)
    6. \(m\angle ACB\)

    Знайти значення\(x\) і/або\(y\) в\(\bigodot A\).

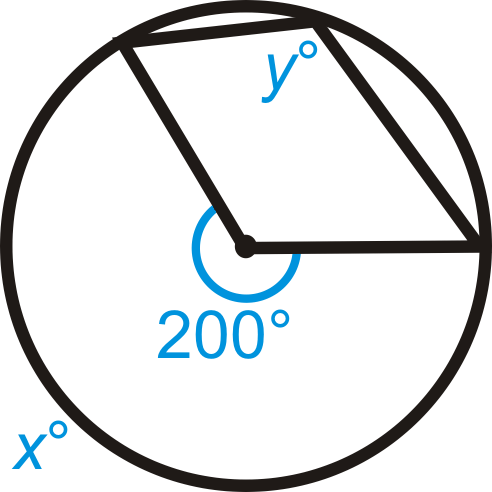
    1. F-д_е5c6113c5f81b51a1A1b335af83993БББФ 54ф 2020 ЕЕЕД 687d985C21A+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
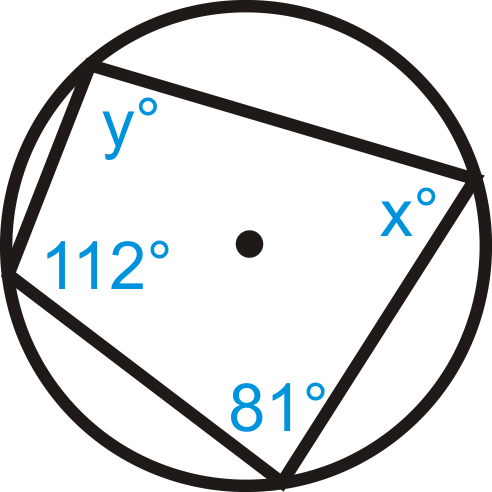
    2. F-D_6 ЕЕД Д 2059d1d9EB ФС81Е7ДФ42693C5Ф93332А5Б3Д 846355D840C85+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
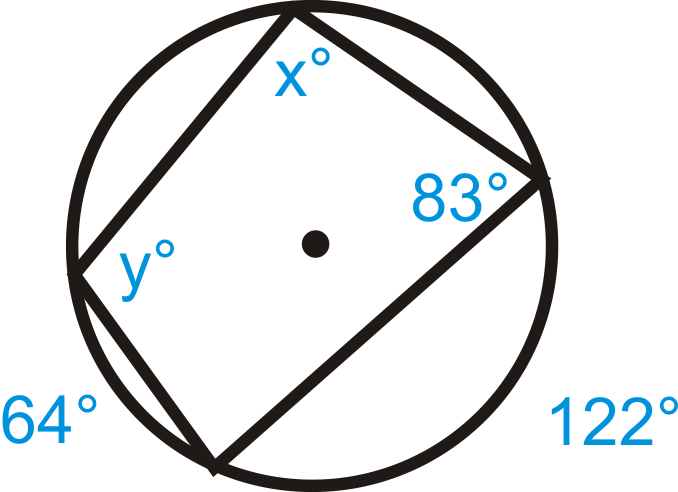
    3. F-D_0652AC7 CCF 2739E340734A85A42 де 79C2CE279E0970E3F4844DE4115+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)

    Вирішити для\(x\).

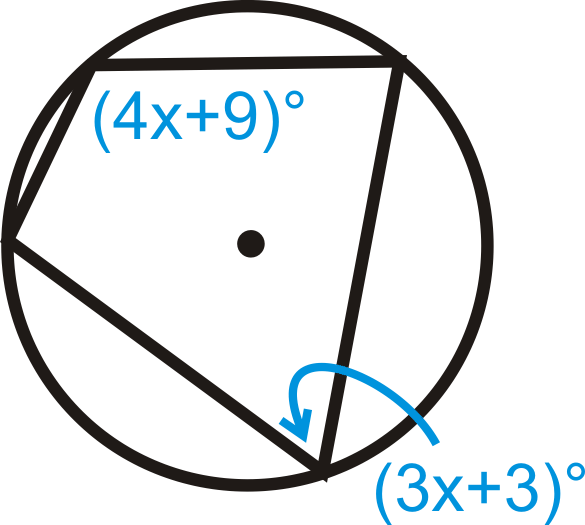
    1. Ф-д_4С1ДФ032БФ 17250331001E38694Б77100784E74570D46982B9061952+зображення_крихіткий+зображення_крихіткий_png
      Малюнок\(\PageIndex{12}\)
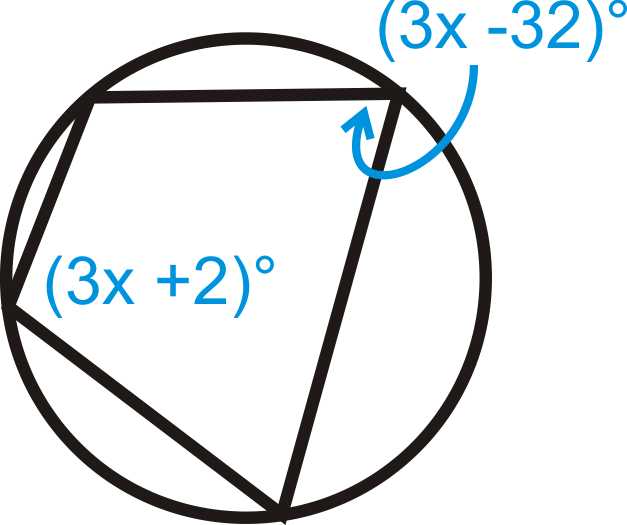
    2. Ф-Д_2365С18ФД60ФД2Б 0361Е3 ЕФ 433ФБД5А 400423169540C3C1D6ABC3E0+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)

    Лексика

    Термін Визначення
    центральний кут Кут, утворений двома радіусами і вершина якого знаходиться в центрі кола.
    акорд Відрізок лінії, кінцеві точки якого знаходяться на колі.
    коло Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    вписаний кут Кут з його вершиною на колі і сторони якого є хордами.
    перехоплена дуга Дуга, яка знаходиться всередині вписаного кута і кінцеві точки якої знаходяться на куті.
    радіус Відстань від центру до зовнішнього обідка кола.
    Вписаний багатокутник Вписаний багатокутник - це багатокутник з кожною вершиною на заданому колі.
    Вписана теорема чотирикутника Теорема про вписаний чотирикутник стверджує, що чотирикутник може бути вписаний в коло тоді і лише тоді, коли протилежні кути чотирикутника є додатковими.
    Циклічні чотирикутники Циклічний чотирикутник - це чотирикутник, який можна вписати в коло.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи вписаних чотирикутників у колах - Основні

    Діяльність: Вписані чотирикутники в колах Дискусійні питання

    Навчальні посібники: Вписані в кола навчальний посібник

    Практика: Вписані чотирикутники в колах

    Реальний світ: Схід сонця в Стоунхенджі