Skip to main content
LibreTexts - Ukrayinska

6.14: Вписані кути в колах

  1. Last updated
  2. Save as PDF
  • Page ID
    54475

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Вершина на колі та хорди як сторони, і чия міра дорівнює половині перехопленої дуги.

    Вписаний кут - це кут з його вершиною на колі і сторони якого є хордами. Перехоплена дуга - це дуга, яка знаходиться всередині вписаного кута і кінцеві точки якої знаходяться на куті. Вершина вписаного кута може знаходитися в будь-якому місці кола до тих пір, поки його сторони перетинають коло, утворюючи перехоплену дугу.

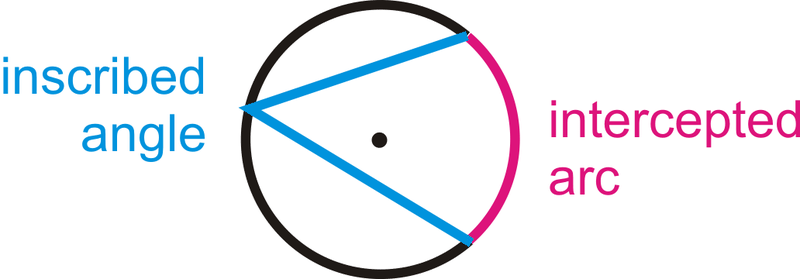
    F-D_3BE91 КА0626641Е19Ф262 САА 83422Д27КС63Е8Д1Ф158Б0Д5845CD1D8+зображення_крихіткий+зображення_крихіткий_крошечкий.PNG
    Малюнок\(\PageIndex{1}\)

    Теорема про вписаний кут стверджує, що міра вписаного кута є половиною міри його перехопленої дуги.

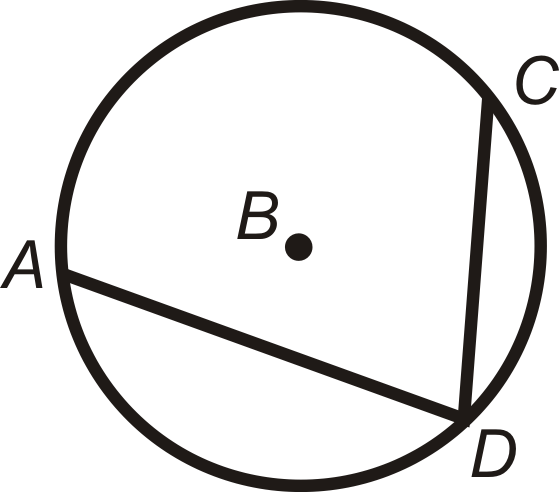
    F-D_03301F1CA98D0947 ЕЕ4ББ 63А630ЕАА689С142862Б01С2397AE6592DC зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    \(m\angle ADC=\dfrac{1}{2}m\widehat{AC}\)і\(m\widehat{AC}=2m\angle ADC\)

    Вписані кути, які перехоплюють одну і ту ж дугу, є конгруентними. Це називається теоремою конгруентних вписаних кутів і показано нижче.

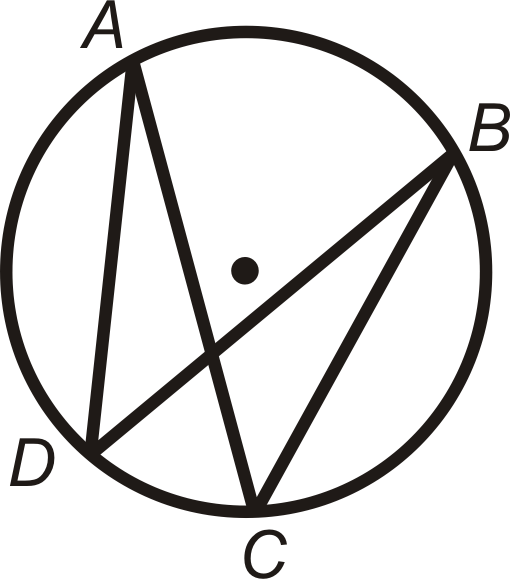
    F-д_717d0c22cdd82737e520a28508A Додати Ф7770477FA48172AC0c0c6517912+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{3}\)

    \(\angle ADB\)і\(\angle ACB\) перехопити\(\widehat{AB}\), так\(m\angle ADB=m\angle ACB\). Точно так само\(\angle DAC\) і\(\angle DBC\)\(\widehat{DC}\) перехоплюють, так\(m\angle DAC=m\angle DBC\).

    Кут перехоплює півколо тоді і тільки тоді, коли це прямий кут (Теорема півкола). У будь-який час, коли прямий кут вписаний в коло, кінцеві точки кута є кінцевими точками діаметра, а діаметр - гіпотенуза.

    Що робити, якщо у вас було коло з двома акордами, які мають спільну кінцеву точку? Як ви могли використовувати дугу, утворену цими акордами, щоб визначити міру кута, який ці хорди роблять всередині кола?

    Приклад\(\PageIndex{1}\)

    Знайти\(m\widehat{DC}\) і\(m\angle ADB\).

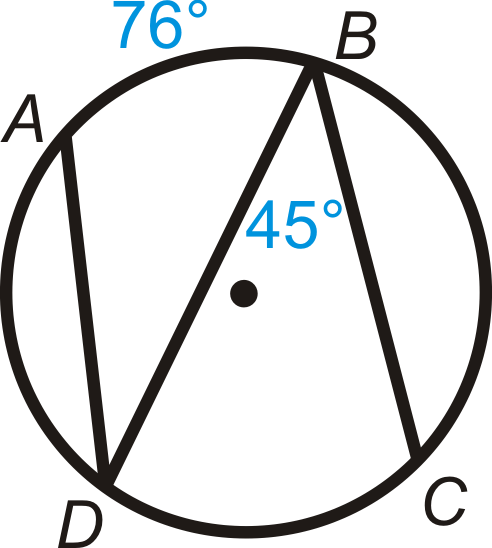
    F-д_2Ф1С5Ф313064А5Е049Д5Е8Ф5ЕФК62Б813567516А1962C9Баба5413A+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    З теореми про вписаний кут:

    \(\begin{aligned} m\widehat{DC}&=2\cdot 45^{\circ}=90^{\circ} \\ m\angle ADB&=12\cdot 76^{\circ}=38^{\circ}\end{aligned}\)

    Приклад\(\PageIndex{2}\)

    Знайти\(m\angle ADB\) і\(m\angle ACB\).

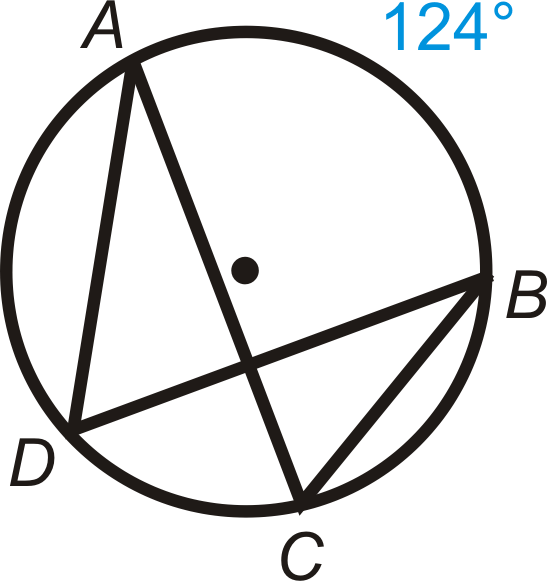
    F-Д_Д085Ф3ФД86Б2Д80Ф32Д09Е7 БББ5027А30Ф384Е3БД 02Ф36434Б4д+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Перехоплена дуга для обох кутів є\(\widehat{AB}\). Тому

    \(\begin{aligned} m\angle ADB&=12\cdot 124^{\circ}=62^{\circ} \\ m\angle ACB&=12\cdot 124^{\circ}=62^{\circ}\end{aligned}\)

    Приклад\(\PageIndex{3}\)

    Знайти\(m\angle DAB\) в\(\bigodot C\).

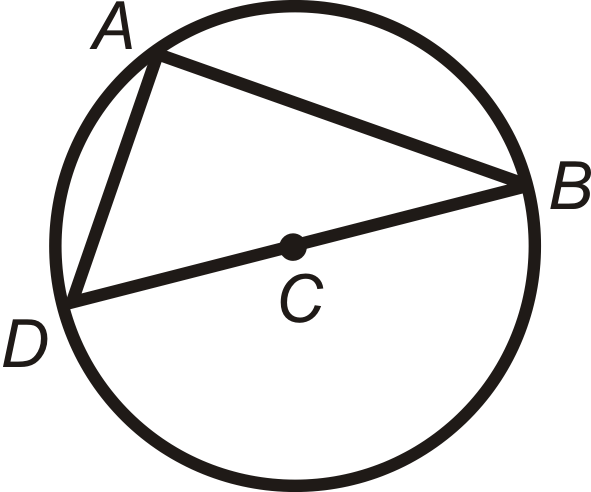
    Ф-д_А33Ф73Е73852Д47Б79023А473ФФ 193Е3БФ 4КД 71С943 ФДД3С3330+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    С - центр,\(\overline{DB}\) так і діаметр. \(\angle DAB\)кінцеві точки знаходяться на діаметрі, так що центральний кут є\(180^{\circ}\).

    \(m\angle DAB=\dfrac{1}{2}\cdot 180^{\circ}=90^{\circ}\).

    Приклад\(\PageIndex{4}\)

    Заповніть бланк: Вписаний кут - ____________ міра перехопленої дуги.

    Рішення

    половина

    Приклад\(\PageIndex{5}\)

    Заповніть бланк: Центральний кут - ________________ міра перехопленої дуги.

    Рішення

    дорівнює

    Рецензія

    Заповніть заготовки.

    1. Кут, вписаний в ________________ є\(90^{\circ}\).
    2. Два вписаних кута, які перехоплюють одну і ту ж дугу - _______________.
    3. Сторони вписаного кута - ___________________.
    4. Намалюйте вписаний кут\(\angle JKL\) в\(\bigodot M\). Потім намалюйте центральний кут\(\angle JML\). Як співвідносяться два кути?

    Знайти значення\(x\) і/або\(y\) в\(\bigodot A\).

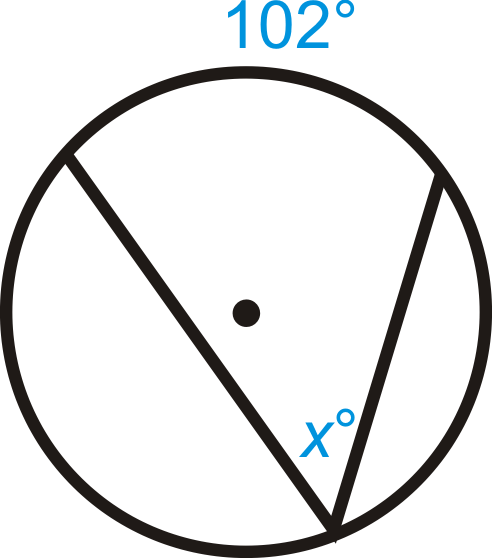    1. F-д_БФБ9С8А391С243Б5А7Ф5С4С72321 Ба02961 ФФД 246491FF7F04435A77+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{7}\)
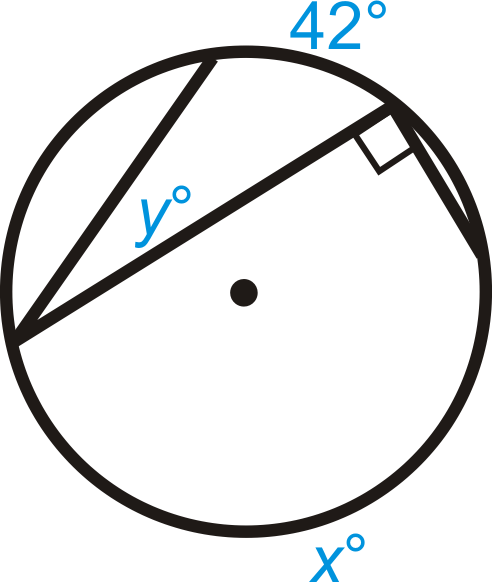    2. F-D_19A1 BEA24832CC8D8DEEE2692D8022 EBFE 08182 ФА0ПКД1AC0CE89C5+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{8}\)
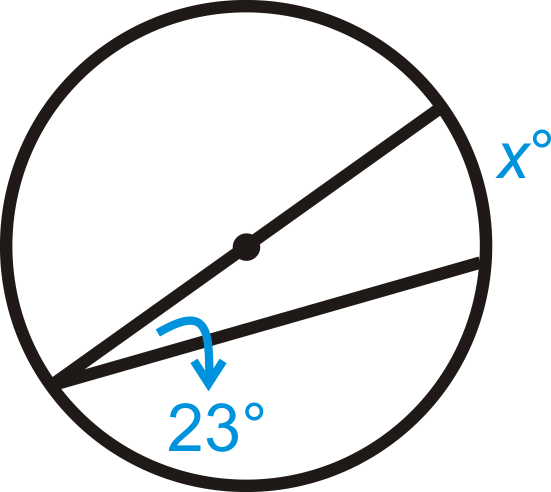    3. F-D_A451216D9Ф 53242Ф53АД 456 БББ 6ДЕ05ДДЕ81АЕ1Ф8352 АФ2Д7БА2Б9+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{9}\)
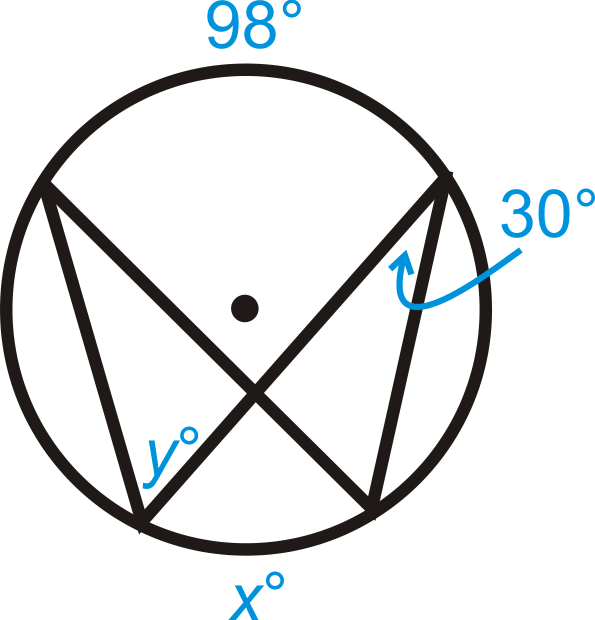    4. Ф-д_638 фа6Б0ФБ9Д5Д75630С806ББ 7 ліжко 01с7ф6д1180Б92654C324425CD+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{10}\)
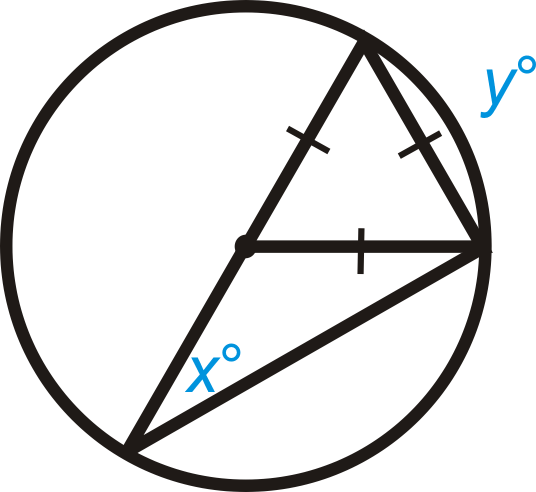    5. F-D_47 БДФ 7156С9Д77100Д338Б4576 С7Ф8Ф6Д40Б1АЕБ55АС616Б7С11С3+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{11}\)

    Вирішити для\(x\).

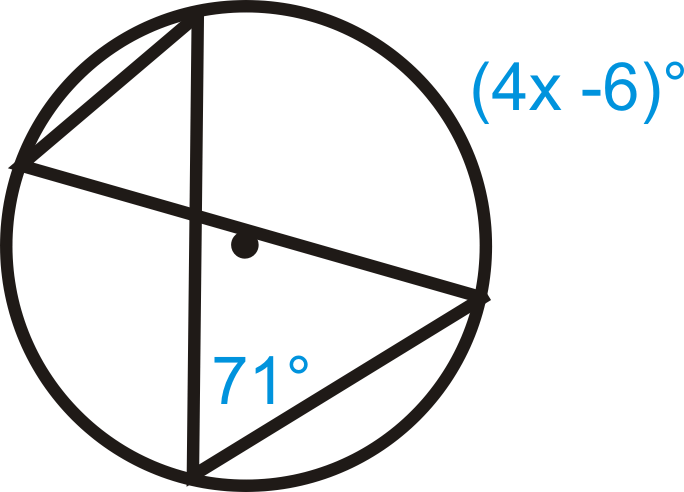    1. F-д_607861 постійного струму 46E4880E7A86 ФД7Д4149ЕФ 46517А80Е2А7E41E07924D+зображення_крихіткий+зображення_крихіткий_крихіткий.PNGМалюнок\(\PageIndex{12}\)
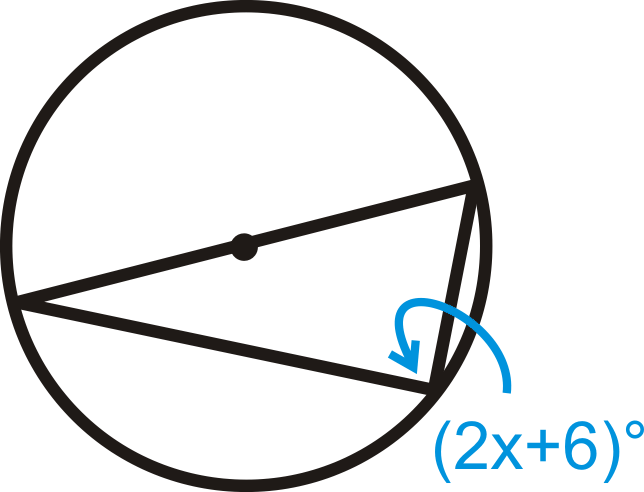    2. F-д_Е2Б989Е1759Б074А31534Ф1Б7Б6749 ФА066Ф4ДБ19Ф14ЕФ18АФДБ6+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{13}\)
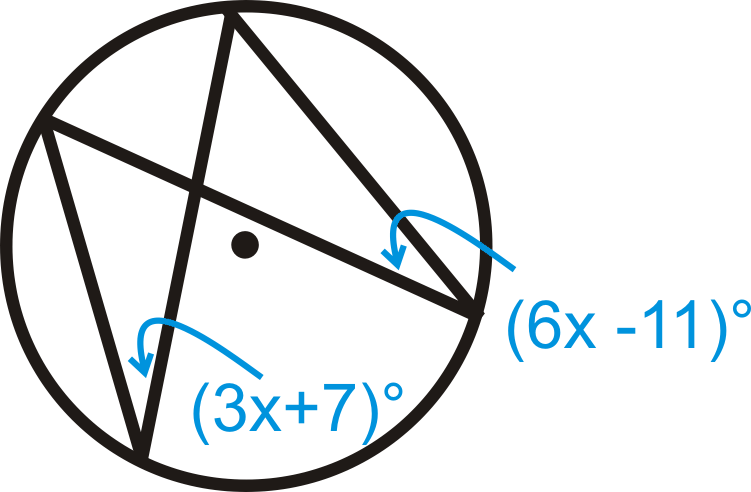    3. F-д_9721891Б7 АБФ Б8Б8ФД91Б688 ЕЕ12А3Ф3353С1666Е6 АБС63Д556478E4+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{14}\)
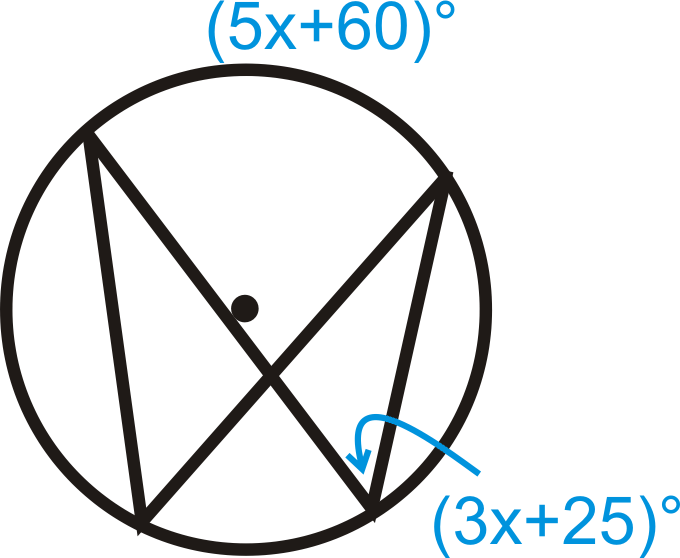    4. F-D_C5858E28E 3А582СБ5Ф2742А8 де 0А4Е3537Е99 ДД50Д542 ДДДД 82AE7F+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{15}\)
    5. Заповніть пробіли доказу теореми про вписаний кут.
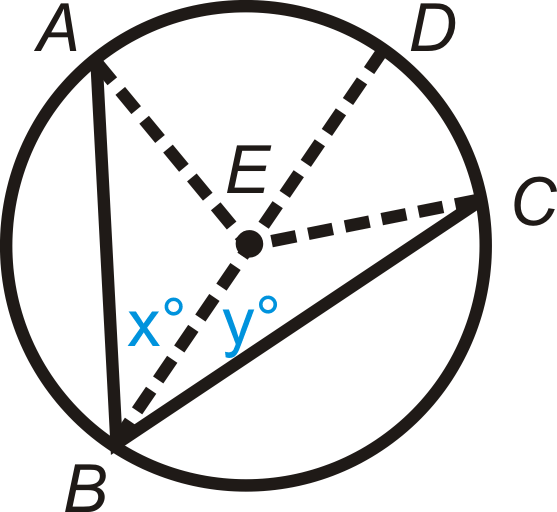      F-D_9 CFC 75FFC 6086EFE5FA 6 компакт-дисків DB1 Def7b357c513272F7819A45E28D899+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{16}\)

    Задано: Вписаний\(\angle ABC\) і діаметр\(\overline{BD}\)

    Доведіть:\ (м\ кут ABC = 12m\ widehat {AC}

    Заява Причина

    1. Вписаний\(\angle ABC\) і діаметр\(\overline{BD}\)

    \(m\angle ABE=x^{\circ}\)і\(m\angle CBE=y^{\circ}\)

    		 1.
    2. \(x^{\circ}+y^{\circ}=m\angle ABC\) 2.
    3. 3. Всі радіуси конгруентні
    4. 4. Визначення рівнобедреного трикутника
    5. \(m\angle EAB=x^{\circ}\)і\(m\angle ECB=y^{\circ}\) 5.
    6. \(m\angle AED=2x^{\circ}\)і\(m\angle CED=2y^{\circ}\) 6.
    7. \(m\widehat{AD}=2x^{\circ}\)і\(m\widehat{DC}=2y^{\circ}\) 7.
    8. 8. Постулат додавання дуги
    9. \(m\widehat{AC}=2x^{\circ}+2y^{\circ}\) 9.
    10. 10. Розподільна PoE
    11. \(m\widehat{AC}=2m\angle ABC\) 11.
    12. \(m\angle ABC=\dfrac{1}{2}m\widehat{AC}\) 12.

    Лексика

    Термін Визначення
    центральний кут Кут, утворений двома радіусами і вершина якого знаходиться в центрі кола.
    акорд Відрізок лінії, кінцеві точки якого знаходяться на колі.
    коло Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    Вписаний кут Вписаний кут - це кут з його вершиною на колі. Міра вписаного кута - половина міри його перехопленої дуги.
    перехоплена дуга Дуга, яка знаходиться всередині вписаного кута і кінцеві точки якої знаходяться на куті.
    радіус Відстань від центру до зовнішнього обідка кола.
    Дуга Дуга - це ділянка окружності кола.
    Перехоплює Перехоплення кривої - це місця, де крива перетинає осі x та y. Перехоплення x - це точка, в якій крива перетинає вісь x. Перехоплення y - це точка, в якій крива перетинає вісь y.
    Теорема про вписаний кут Теорема про вписаний кут стверджує, що міра вписаного кута є половиною міри його перехопленої дуги.
    Теорема про півколо Теорема півкола стверджує, що кожен раз, коли прямий кут вписаний в коло, кінцеві точки кута є кінцевими точками діаметра, а діаметр - гіпотенуза.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи вписаних кутів в колах - Основні

    Діяльність: Вписані кути в колах Дискусійні питання

    Навчальні посібники: Вписані в кола навчальний посібник

    Практика: Вписані кути в колах