Skip to main content
LibreTexts - Ukrayinska

6.13: Відрізки від акордів

  1. Last updated
  2. Save as PDF
  • Page ID
    54447

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Застосуйте теорему про перетинаються хорди.

    Коли у нас є дві хорди, які перетинаються всередині кола, як показано нижче, два трикутники, які в результаті, схожі.

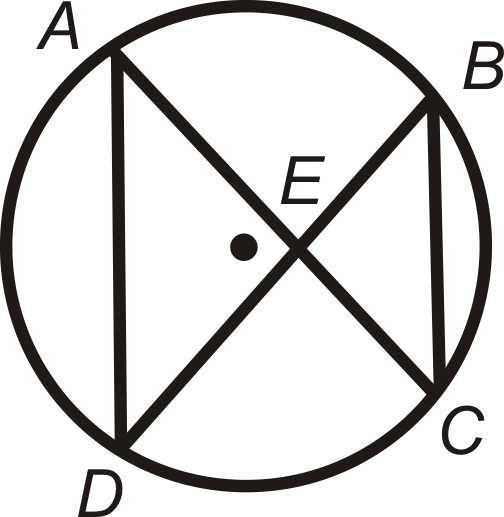
    F-D_4CC постійного струму фа0837f21344d535e0cbff6f1d0d5a60b614f2cbd8ddf331803+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Це робить відповідні сторони в кожному трикутнику пропорційними і призводить до співвідношення між сегментами хорд, як зазначено в Теоремі про перетинаються хорди.

    Теорема про перетинаються хорди: Якщо дві хорди перетинаються всередині кола так, що один розділяється на відрізки довжини a і b, а інший на відрізки довжини,\(c\) а\(d\) потім\(ab=cd\).

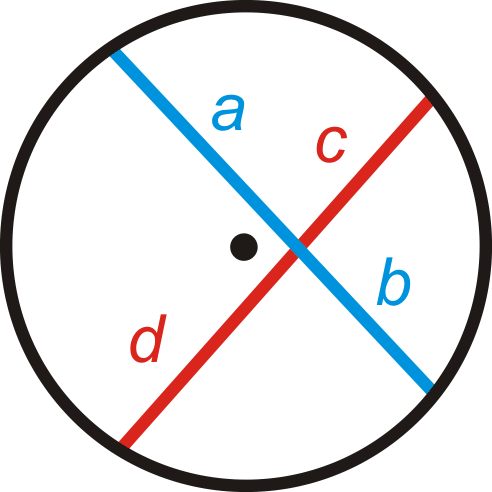
    Ф-Д_БД 79049 ФА98Ф 6Е6Е1CF65C408132 АБФ 252С270Ф26АБЕД 023C80F801+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Що робити, якщо вам дали коло з двома акордами, які перетинаються один з одним? Як можна використовувати довжину деяких відрізків, утворених їх перетином, для визначення довжин невідомих відрізків?

    Приклад\(\PageIndex{1}\)

    Знайти\(x\). Спрощуйте будь-які радикали.

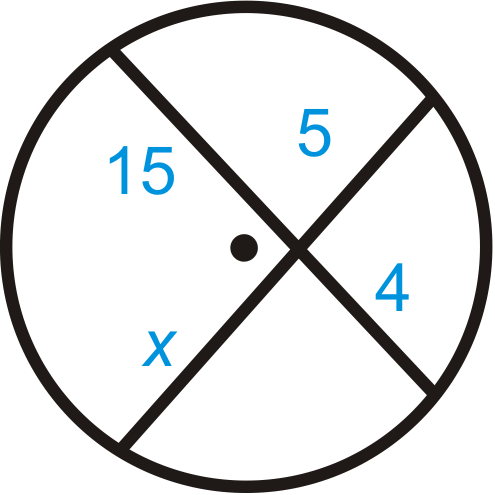
    F-д_С0ДБ90 АФ 16124295С0А755д0 ЕЦ27С53Ф981А10Д60Д5С9ДК03424 Беб+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Використовуйте теорему про перетинаються хорди.

    \(15\cdot 4=5\cdot x\)

    \(60=5x\)

    \(x=12\)

    Приклад\(\PageIndex{2}\)

    Знайти\(x\). Спрощуйте будь-які радикали.

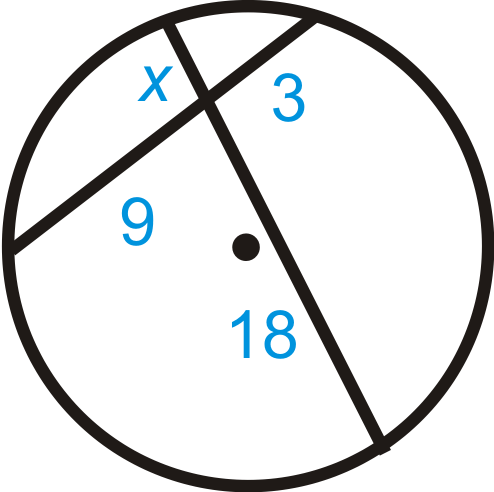
    F-D_F4547490566F674 ефект 2B06538d8d91E34E468A3B0696D73518BD68+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{4}\)

    Рішення

    Використовуйте теорему про перетинаються хорди.

    \(\begin{aligned} 18\cdot x&=9\cdot 3 \\ 18x&=27 \\ x&=1.5\end{aligned}\)

    Приклад\(\PageIndex{3}\)

    Знайдіть x на кожній діаграмі нижче.

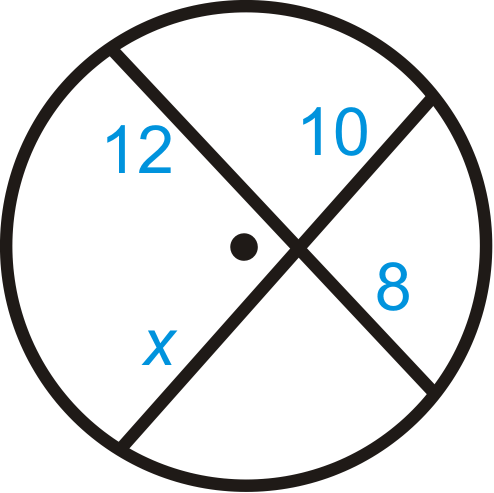
    1. Ф-д_5С60692 Ф56058607Ф8028САА 60Ф18Б174Д74 Ліжко 0Д8Ф3107209D32E+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{5}\)
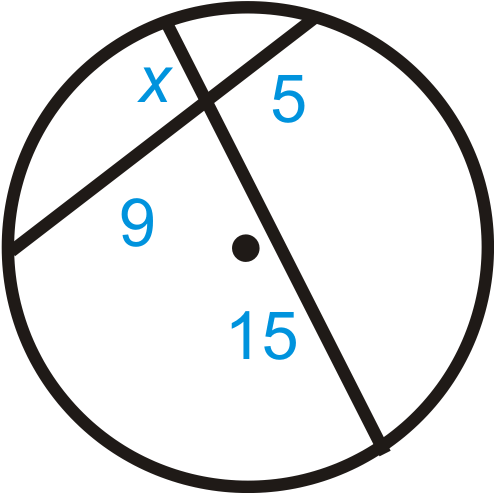
    2. F-D_8D4A4А 4364С7906791 С466271377А283Ф0 CAEF8Ф8Ф8ФБ944337BFDD68+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\ (\ Індекс сторінки {6}\

    Рішення

    1. Використовуйте формулу з теореми про перетинаються хорди.

    \(\begin{aligned}12\cdot 8 &=10\cdot x \\ 96&=10x \\ 9.6&=x\end{aligned}\)

    1. Використовуйте формулу з теореми про перетинаються хорди.

    \(\begin{aligned} x\cdot 15&=5\cdot 9 \\ 15x&=45 \\ x&=3 \end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Вирішіть для\(x\) кожної діаграми нижче.

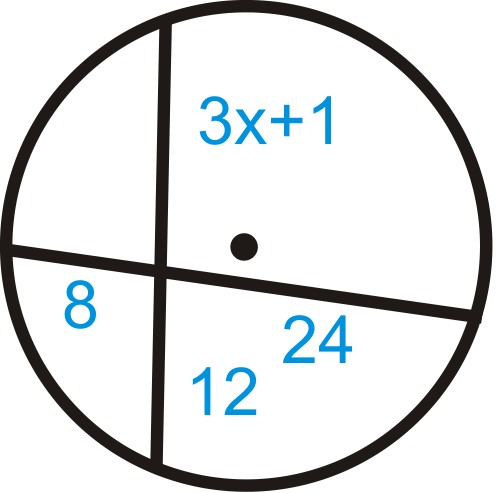
    1. F-д_Б8462186 де 5521 СА85Б40А2 ЕДС295А1Е0Е9С2КБФ34А06ФАФД+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
    2. F-д_Б8462186 де 5521 СА85Б40А2 ЕДС295А1Е0Е9С2КБФ34А06ФАФД+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)

    Рішення

    1. Використовуйте теорему про перетинаються хорди.

    \(\begin{aligned} 8\cdot 24&=(3x+1)\cdot 12 \\192&=36x+12 \\ 180&=36x \\ 5&=x\end{aligned}\)

    1. Використовуйте теорему про перетинаються хорди.

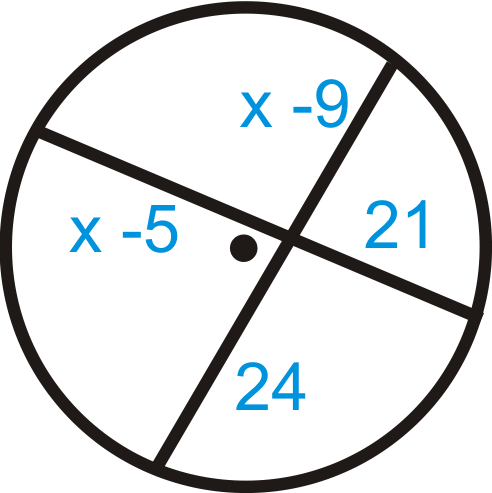
    \(\begin{aligned} (x−5)21&=(x−9)24 \\ 21x−105&=24x \\ 111&=3x \\ 37−216&=x \end{aligned}\)

    Приклад\(\PageIndex{5}\)

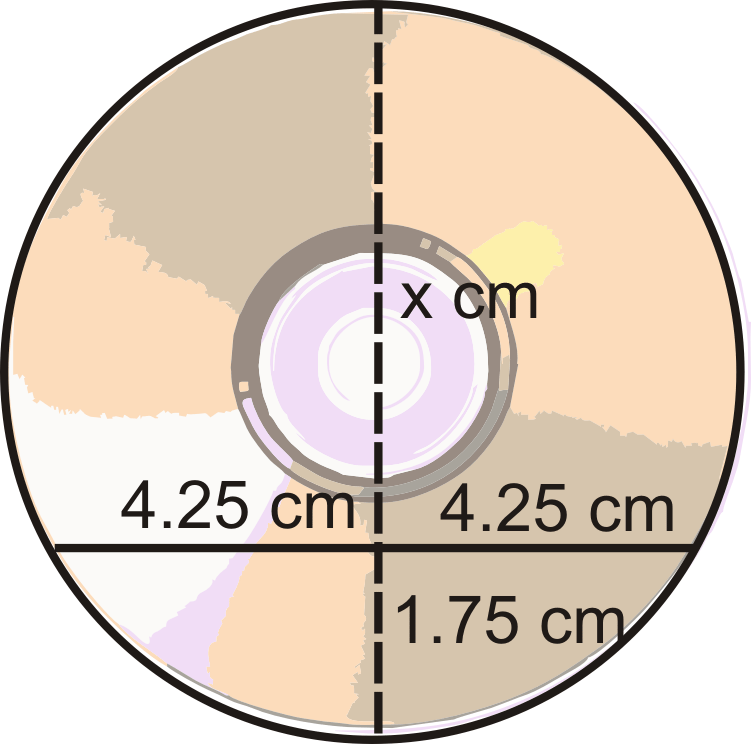
    Ізмаїл знайшов зламаний шматок компакт-диска в своїй машині. Він розміщує лінійку поперек двох точок на обідку, а довжина хорди дорівнює 9,5 см. Відстань від середини цієї хорди до найближчої точки на обідку становить 1,75 см. Знайдіть діаметр CD.

    F-D_1814FF05A8C6E812551d5C51B0A630E4B6716FF Каб 2B0351099933BD+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)

    Рішення

    Подумайте про це як про дві акорди, що перетинаються один з одним. Якби ми продовжили відрізок 1,75 см, це був би діаметр. Отже, якщо ми знайдемо х на схемі нижче і додамо його до 1,75 см, ми б знайшли діаметр.

    \(\begin{aligned} 4.25\cdot 4.25&=1.75\cdot x \\ 18.0625&=1.75x\end{aligned}\)

    \(x\approx 10.3 cm, making the diameter 10.3+1.75\approx 12 cm, which\: is\: the actual diameter of a CD.\)

    F-д_Е85Ф581549471BE4B7F07C5C1CF94D11FF502b70BDEF5F3F9C4572C0+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)

    Рецензія

    Заповніть пропуски для кожної задачі нижче, а потім вирішіть для відсутнього відрізка.

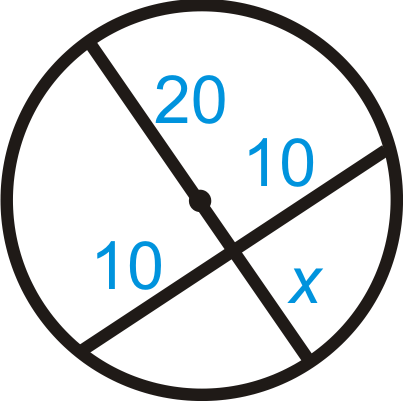
    1. F-D_F33C11 АФ 5D671646606DC 3255E012C7 Fea998A8BF8F01CF39A25966+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)

    \(20x=_______\)

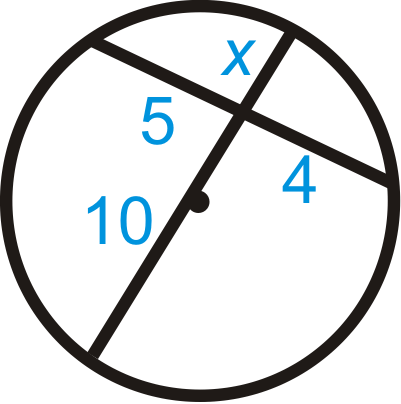
    1. F-д_Е44А 5040040Б79ЕБ638 СБ098 Фе 1 Дек 8д 0де 471 ББ 4де9078A92cd146+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)

    \(\text{_______}\cdot 4=\text{_______}\cdot x\)

    Знайдіть x на кожній діаграмі нижче. Спрощуйте будь-які радикали.

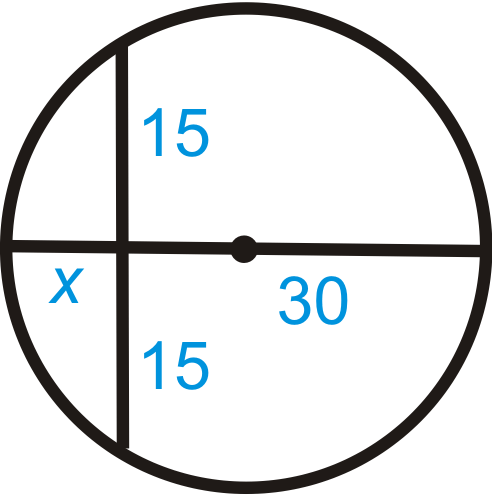
    1. Ф-д_13Д0Ф4С44Б1026Б7Е052ДА5Ф162А10АА10АА5362Ф1Е7423ЕФ72А9Ф75+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
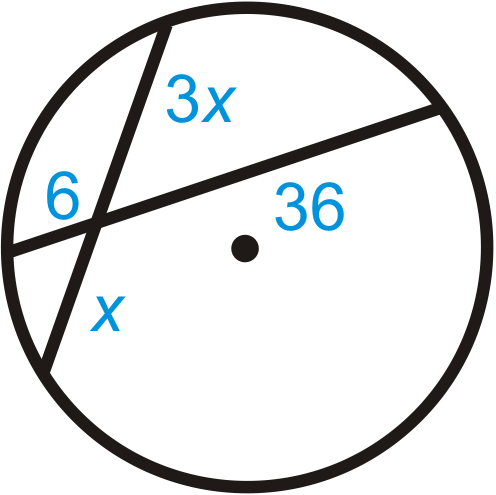
    2. Ф-Д_БД39Б7Ф92ДБ 63ДБ 1ДБ 800043Б06349277235975Е6Д24FFDA2AAE7+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
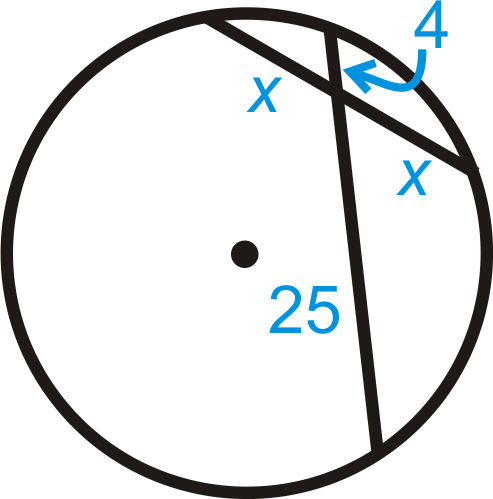
    3. F-D_542 АЦБ 84005Б8С6181194Е8 А1Ф33436ФДЕ8ДД 81Д75Б8С66АЦ593ЕДДДБКА+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)

    Знайдіть значення\(x\).

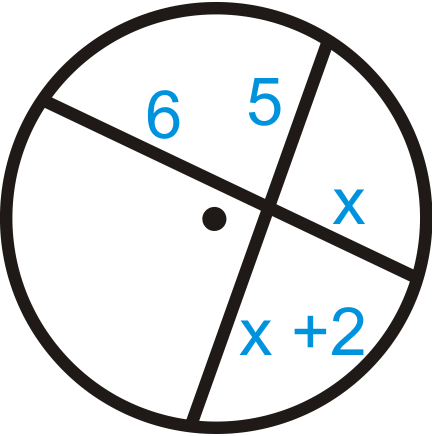    1. F-D_DC2DE 70D BEA88A7395338 ABB6D84357954 AEAFB364AED9BE4461F1+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{16}\)
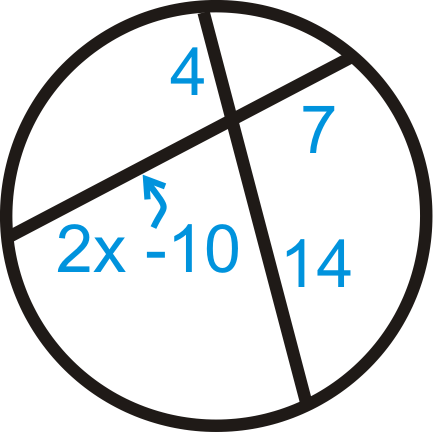
    2. Ф-Д_4Е6 А4Ф 85788888Е 000365А49Д034А6А50130А4А412Д5788А6335Е0709+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)
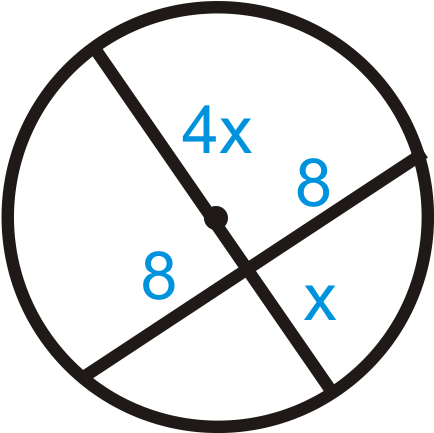
    3. Ф-Д_Б11А311206 ФК8 БББ 07С44А06Б7ЕС659Ф54468А713АЕ98CEF9298E3F7D+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)
    4. Сьюзі знайшла шматок зламаної тарілки. Вона розміщує лінійку через дві точки на обідку, а довжина хорди становить 6 дюймів. Відстань від середини цієї хорди до найближчої точки на обідку становить 1 дюйм. Знайдіть діаметр пластини.
    5. Заповніть пробіли доказу теореми про перетинаються хорди.
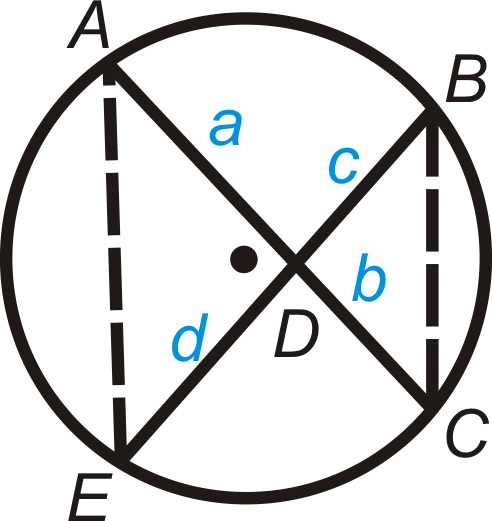
      Ф-Д_0Е457Е39 АБ 019Е060Б739СА2СА84КБ9630ЕБЦФ21БКБ8АЦ9Б1+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)

    Дано: Перетинаються акорди\(\overline{AC}\) і\(\overline{BE}\).

    Доведіть:\(ab=cd\)

    Заява Причина
    1. Перетинаються акорди\(\overline{AC}\) і\(\overline{BE}\) з відрізками\(a\)\(b\),\(c\),, і\(d\). 1.
    2. 2. Теорема про конгруентні вписані кути
    3. \(\Delta ADE\sim \Delta BDC\) 3.
    4. 4. Відповідні частини подібних трикутників пропорційні.
    5. \(ab=cd\) 5.

    Лексика

    Термін Визначення
    центральний кут Кут, утворений двома радіусами і вершина якого знаходиться в центрі кола.
    акорд Відрізок лінії, кінцеві точки якого знаходяться на колі.
    коло Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    вписаний кут Кут з його вершиною на колі і сторони якого є хордами.
    перехоплена дуга Дуга, яка знаходиться всередині вписаного кута і кінцеві точки якої знаходяться на куті.
    радіус Відстань від центру до зовнішнього обідка кола.
    Теорема про перетинаються хорди Відповідно до теореми, що перетинаються хорди, якщо дві хорди перетинаються всередині кола так, що один розділений на відрізки довжини,\(a\) а\(b\) інший на відрізки довжини\(c\) і\(d\), то\(ab = cd\).

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Відрізки від принципів акордів - Основні

    Діяльність: Відрізки з питань обговорення акордів

    Навчальні посібники: Кола: Сегменти та довжини навчальний посібник

    Практика: Відрізки від акордів