6.12: Акорди та дуги центрального кута

Дуги визначаються кутами, вершина яких є центром кола і хордами (відрізками, що з'єднують дві точки на колі).

Акорди в колах

Теореми про хорди

Існує кілька важливих теорем про акорди, які допоможуть вам краще аналізувати кола.

1. Теорема хорд #1: У одному колі або конгруентних колах незначні дуги конгруентні тоді і лише тоді, коли відповідні акорди є конгруентними.

Малюнок$\PageIndex{1}$

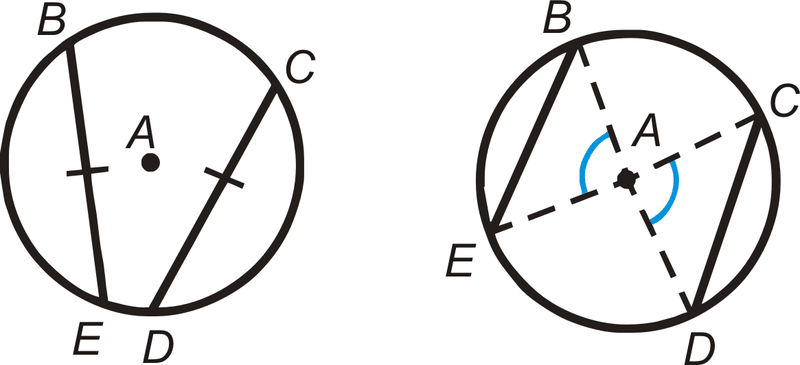
На обох цих картинках$\overline{BE}\cong \overline{CD}$ і$\widehat{BE}\cong \widehat{CD}$.

2. Теорема хорди #2: Перпендикулярна бісектриса хорди також є діаметром.

Малюнок$\PageIndex{2}$

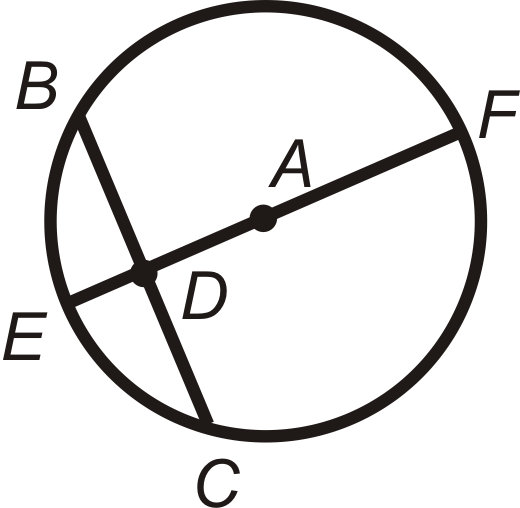
Якщо$\overline{AD}\perp \overline{BC}$ і$\overline{BD}\cong \overline{DC}$$\overline{EF}$ то - діаметр.

3. Теорема хорди #3: Якщо діаметр перпендикулярний хорді, то діаметр бісекції хорди і відповідної їй дуги.

Малюнок$\PageIndex{3}$

Якщо$\overline{EF}\perp \overline{BC}$, то$\overline{BD}\cong \overline{DC}$

4. Теорема хорд #4: У одному колі або конгруентних колах дві акорди конгруентні тоді і лише тоді, коли вони рівновіддалені від центру.

Малюнок$\PageIndex{4}$

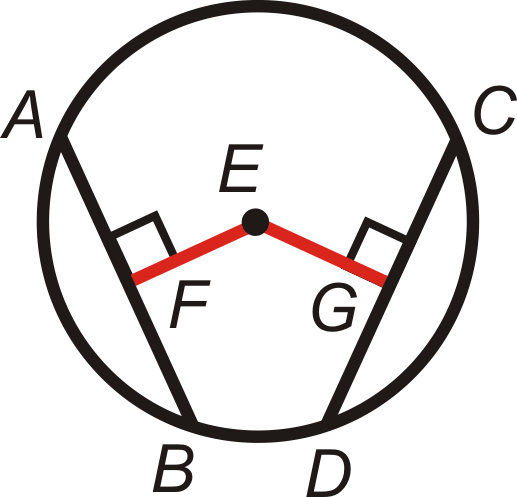
Найкоротша відстань від будь-якої точки до прямої - це перпендикулярна лінія між ними. Якщо$FE=EG$ і$\overline{EF}\perp \overline{EG}$, то$\overline{AB}$ і$\overline{CD}$ рівновіддалені до центру і$\overline{AB}\cong \overline{CD}$.

Що робити, якщо вам дали коло з двома акордами, промальованими через нього? Як ви могли визначити, чи ці два акорди були конгруентними?

Приклад$\PageIndex{1}$

Знайдіть значення$x$ і$y$.

Малюнок$\PageIndex{5}$

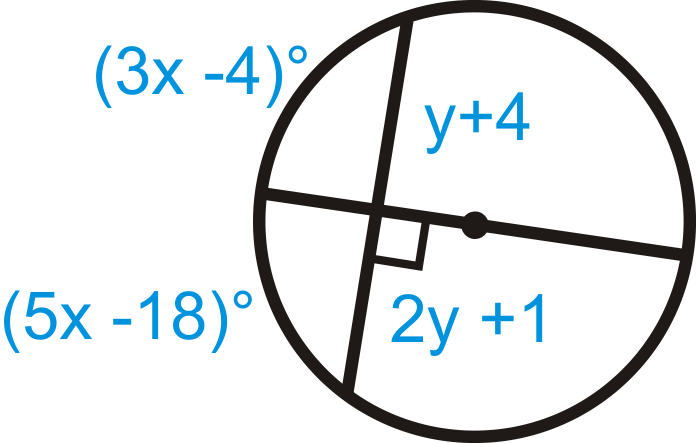
Рішення

Діаметр перпендикулярний хорді, що означає, що вона розсікає хорду і дугу. Налаштування рівнянь для$x$ і$y$.

\ (\ почати {масив} {rlr}
(3 х-4) ^ {\ circ} & =( 5 х-18) ^ {\ circ} & y+4=2 y+1\\
14 & =2 x & 3 = y\\
7 & =x
\ end {масив}\)

Приклад$\PageIndex{2}$

$BD=12$і$AC=3$ в$\bigodot A$. Знайдіть радіус.

Малюнок$\PageIndex{6}$

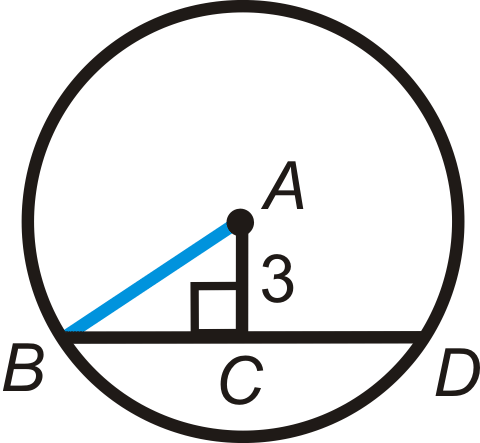
Рішення

Спочатку знайдіть радіус. $\overline{AB}$є радіусом, тому ми можемо використовувати прямокутний трикутник\ Delta ABC\) з гіпотенузою$\overline{AB}$. З теореми акордів #3,$BC=6$.

$\begin{aligned} 3^2+6^2&=AB^2 \\ 9+36&=AB^2 \\ AB&=\sqrt{45}=3\sqrt{5}\end{aligned}$

Приклад$\PageIndex{3}$

Використовуйте$\bigodot A$, щоб відповісти на наступне.

Малюнок$\PageIndex{7}$

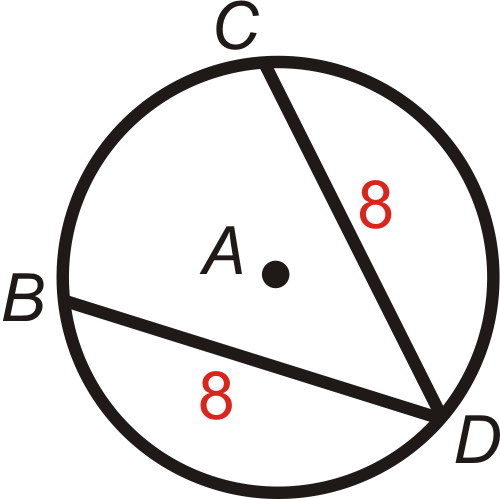
1. Якщо$m\widehat{BD}=125^{\circ}$, знайдіть$m\widehat{CD}$.
2. Якщо$m\widehat{BC}=80^{\circ}$, знайдіть$m\widehat{CD}$.

Рішення

1. $BD=CD$, що означає, що дуги теж конгруентні. $m\widehat{CD}=125^{\circ}$.
2. $m\widehat{CD}\cong m\widehat{BD}$тому що$BD=CD$.

$\begin{aligned} m\widehat{BC}+m\widehat{CD}+m\widehat{BD}&=360^{\circ} \\ 80^{\circ}+2m\widehat{CD}&=360^{\circ} \\ 2m\widehat{CD}&=280^{\circ} \\ m\widehat{CD}=140^{\circ}\end{aligned}$

Приклад$\PageIndex{4}$

Знайдіть значення$x$ і$y$.

Малюнок$\PageIndex{8}$

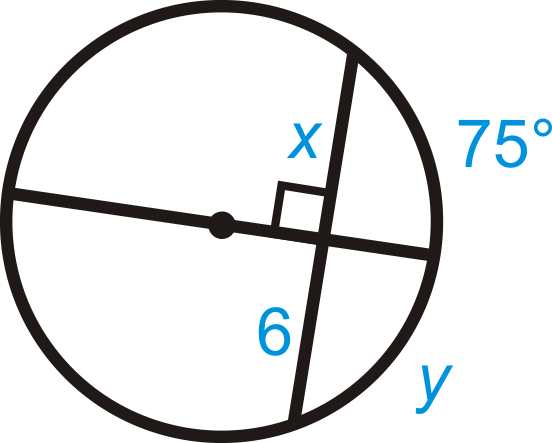
Рішення

Діаметр перпендикулярний хорді. З теореми акордів #3,$x=6$ і$y=75^{\circ}$.

Приклад$\PageIndex{5}$

Знайдіть значення$x$.

Малюнок$\PageIndex{9}$

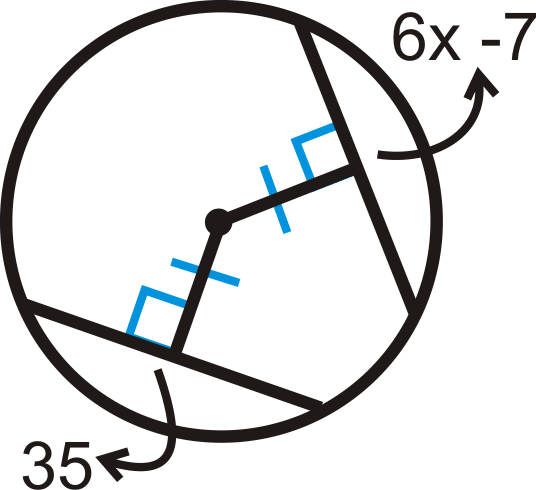
Рішення

Оскільки відстань від центру до акордів дорівнює, акорди конгруентні.

$\begin{aligned} 6x−7&=35 \\ 6x&=42 \\ x&=7 \end{aligned}$

Рецензія

Заповніть заготовки.

Малюнок$\PageIndex{10}$

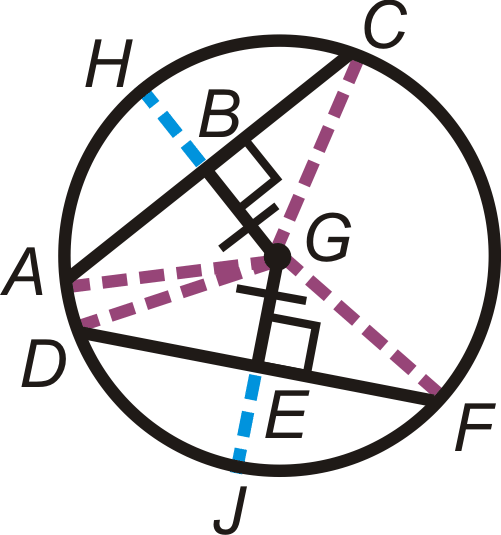
1. $\text{_____}\cong \overline{DF}$
2. $\widehat{AC} \cong \text{_____}$
3. $\widehat{DJ}\cong \text{_____}$
4. $\text{_____}\cong \overline{EJ}$
5. $\angle AGH\cong \text{_____}$
6. $\angle DGF\cong \text{_____}$
7. Перелічіть всі конгруентні радіуси в$\bigodot G$.

Знайти значення зазначеної дуги в$\bigodot A$.

8. $m\widehat{BC}$

   

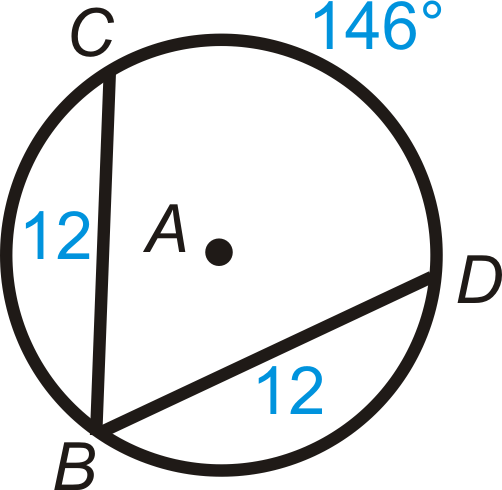
   Малюнок$\PageIndex{11}$

9. $m\widehat{BD}$

   

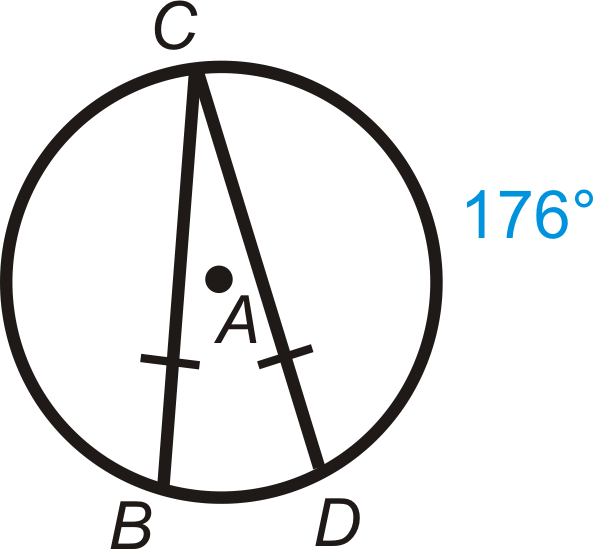
   Малюнок$\PageIndex{12}$

10. $m\widehat{BC}$

    

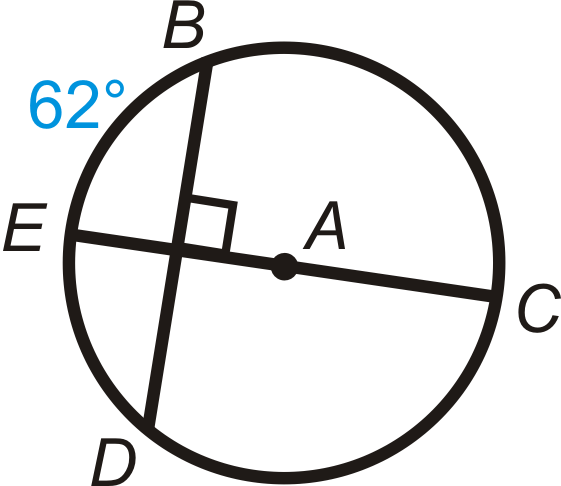
    Малюнок$\PageIndex{13}$

11. $m\widehat{BD}$

    

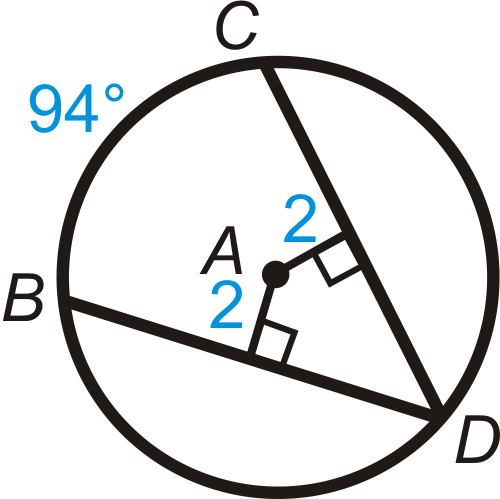
    Малюнок$\PageIndex{14}$

12. $m\widehat{BD}$

    

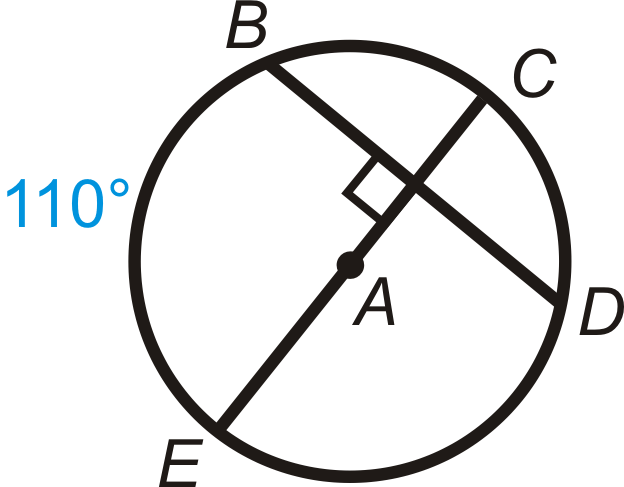
    Малюнок$\PageIndex{15}$

13. $m\widehat{BD}$

    

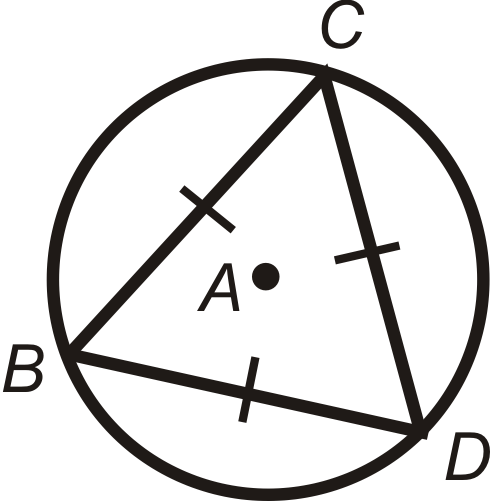
    Малюнок$\PageIndex{16}$

Знайти значення$x$ і/або$y$.

14. 

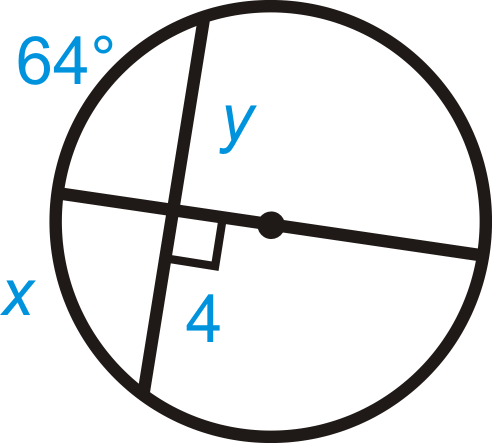
    Малюнок$\PageIndex{17}$

15. 

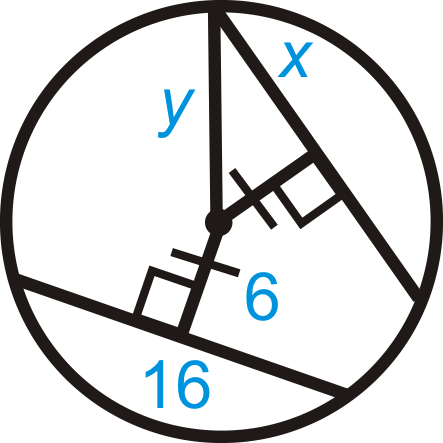
    Малюнок$\PageIndex{18}$

16. 

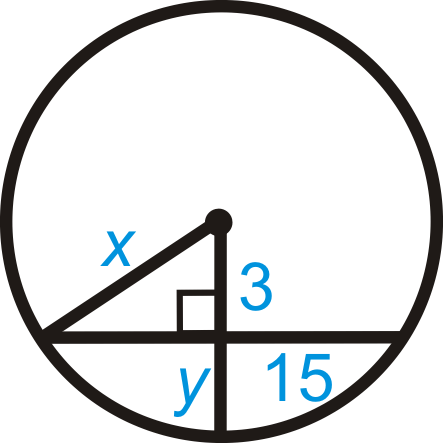
    Малюнок$\PageIndex{19}$

17. $AB=32$

    

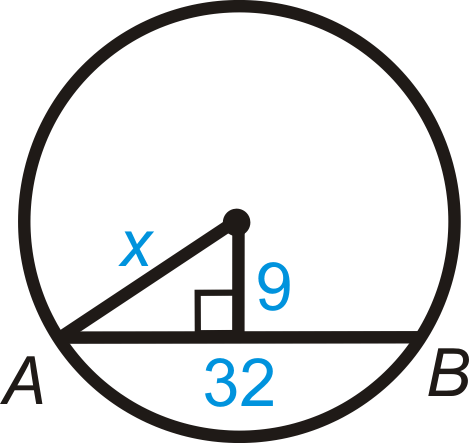
    Малюнок$\PageIndex{20}$

18. 

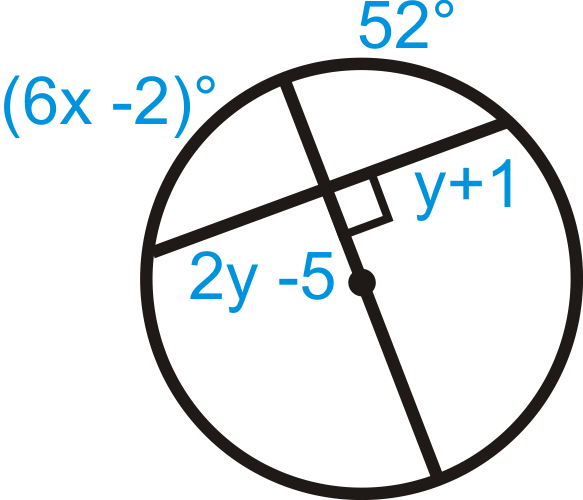
    Малюнок$\PageIndex{21}$

19. 

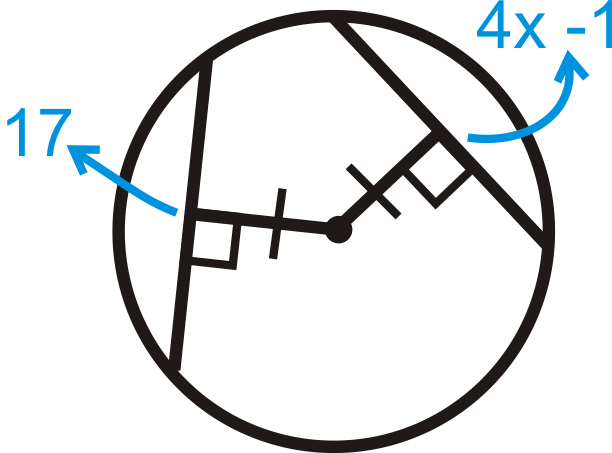
    Малюнок$\PageIndex{22}$

20. 

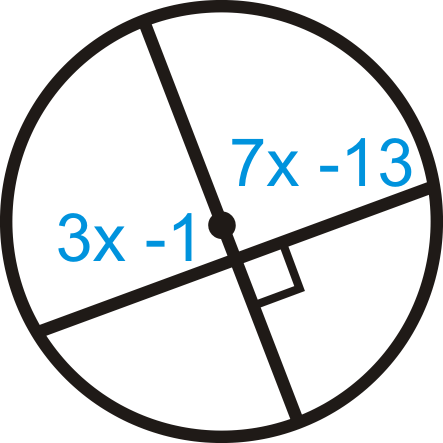
    Малюнок$\PageIndex{23}$

21. 

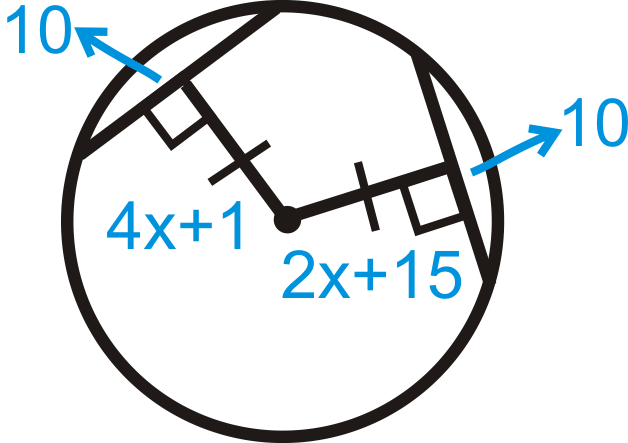
    Малюнок$\PageIndex{24}$

22. $AB=20$

    

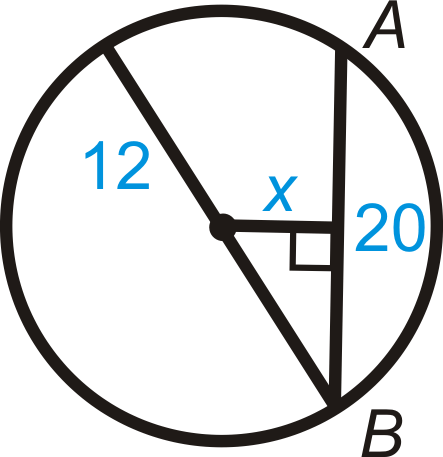
    Малюнок$\PageIndex{25}$

23. Знайти$m\widehat{AB}$ в питанні 17. Округлите відповідь до найближчої десятої частки градуса.
24. Знайти$m\widehat{AB}$ в питанні 22. Округлите відповідь до найближчої десятої частки градуса.

У задачах 25-27, що можна зробити висновок про картину? Викладіть теорему, яка виправдовує вашу відповідь. Можна припустити, що A - це центр кола.

25. 

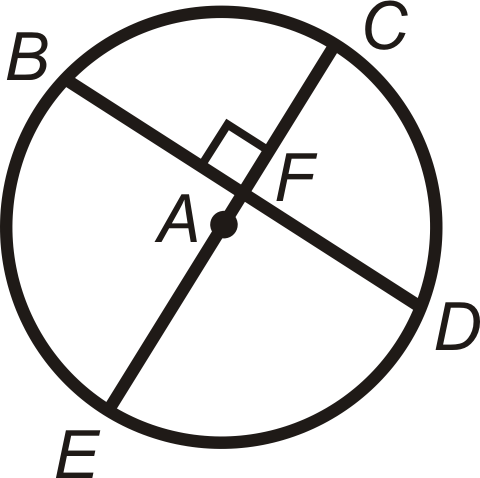
    Малюнок$\PageIndex{26}$

26. 

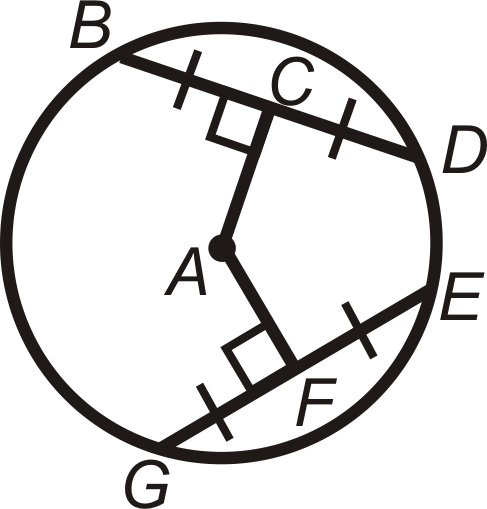
    Малюнок$\PageIndex{27}$

27. 

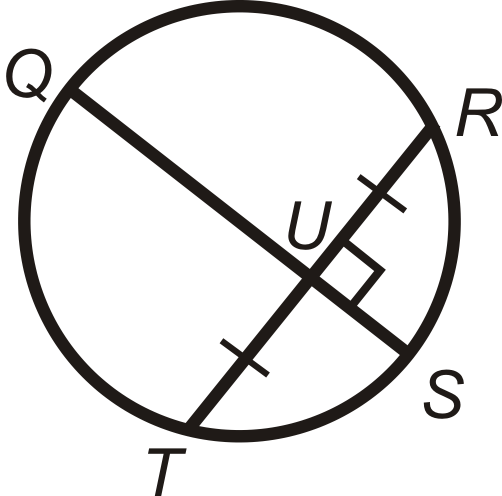
    Малюнок$\PageIndex{28}$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 9.4.

Лексика

Термін	Визначення
акорд	Відрізок лінії, кінцеві точки якого знаходяться на колі.
коло	Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
діаметр	Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
радіус	Відстань від центру до зовнішнього обідка кола.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи акордів в колах - Основні

Види діяльності: Акорди в колах Дискусійні питання

Навчальні посібники: Кола: Сегменти та довжини навчальний посібник

Практика: Акорди та дуги центрального кута