Skip to main content
LibreTexts - Ukrayinska

6.11: Довжина дуги

  1. Last updated
  2. Save as PDF
  • Page ID
    54468

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Частина окружності кола.

    Один із способів вимірювання дуг - в градусах. Це називається «мірою дуги» або «мірою ступеня» (див. Дуги в колах). Дуги також можуть вимірюватися по довжині, як частина окружності. Довжина дуги - це довжина дуги або частини окружності кола. Довжина дуги безпосередньо пов'язана з мірою дуги ступеня.

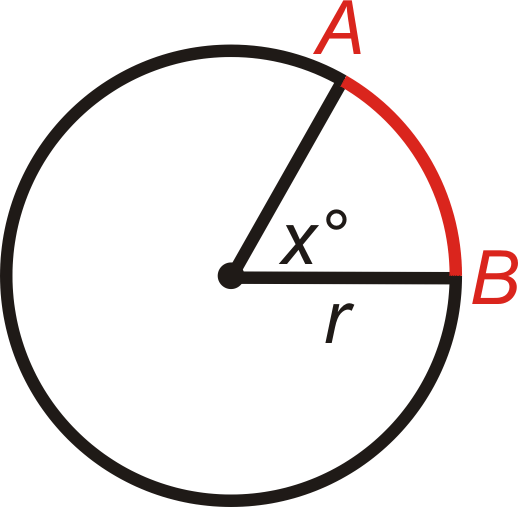
    F-D_D400АЕ 3102 ДК 7Д7А4Ф735ФД7 ДДФ076Д477Б82Ф5Д4С00Д48Д53424+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Формула довжини дуги: Довжина\(\widehat{AB}=\dfrac{m\widehat{AB}}{360^{\circ}}\cdot \pi d\) або\(\dfrac{m\widehat{AB}}{360^{\circ}}\cdot 2\pi r\).

    Що робити, якщо вам дали міру кута дуги кола? Як ви могли знайти довжину цієї дуги?

    Приклад\(\PageIndex{1}\)

    Знайти довжину дуги\(\widehat{PQ}\) в\(\bigodot A\). Залиште свої відповіді з точки зору\(\pi\).

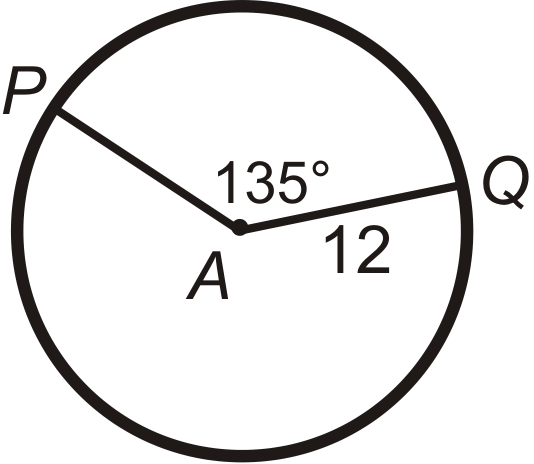
    Ф-д_6д7ф32А12С5Ф95Б741ДБ05Д6Д951Е2Д56С29Ф3951Б14Б0Е8Б10Ф8Ф52+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Скористайтеся формулою довжини дуги.

    \(\begin{aligned} \widehat{PQ}&=\dfrac{135}{360}\cdot 2\pi (12) \\ \widehat{PQ}&=\dfrac{3}{8}\cdot 24\pi \\ \widehat{PQ}&=9\pi \end{aligned}\)

    Приклад\(\PageIndex{2}\)

    Типова велика піца має діаметр 14 дюймів і розрізається на 8 частин. Подумайте про скоринку як про окружність піци. Знайдіть довжину скоринки для всієї піци. Потім знайдіть довжину скоринки для одного шматка піци, якщо вся піца розрізана на 8 частин.

    F-D_16Ф091 АФКА 758 ДД КАФ 412Д6 АД 4Д 72383Е6Д 14934C3C35201CE5532D+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Вся довжина скоринки, або окружність піци, знаходиться\(14\pi \approx 44 in.\) в\(\dfrac{1}{8}\) піці, один шматок мав би\(\dfrac{44}{8}\approx 5.5 inches\) скоринку.

    Приклад\(\PageIndex{3}\)

    Знайти довжину\(\widehat{PQ}\). Залиште свою відповідь з точки зору\(\pi\).

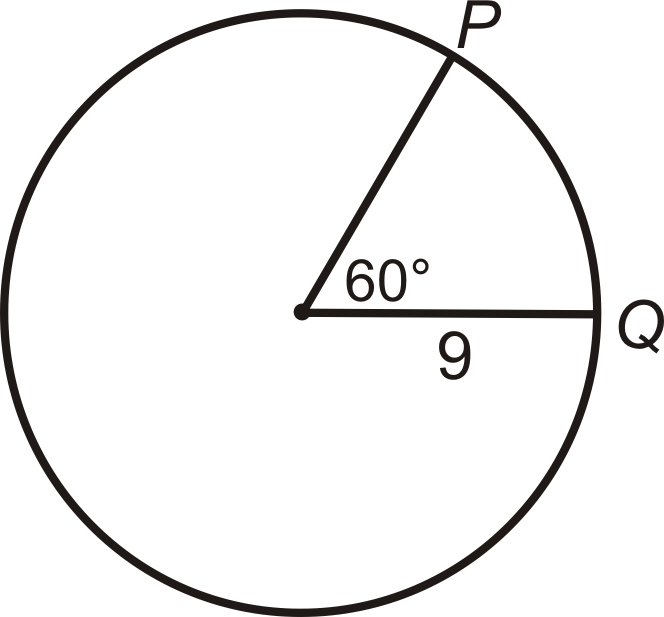
    F-D_09 АС 85Д9 ЕД 382178561Б2Д19С5Ф41Ф894016786 BEF826C16B30C+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    На малюнку центральний кут, який відповідає з\(\widehat{PQ}\) є\(60^{\circ}\). Це означає, що\(m\widehat{PQ}=60^{\circ}\). Подумайте про довжину дуги як частину окружності. Є\(360^{\circ}\) в колі, так що 60^ {\ circ}\) буде 16 з цього (\(60^{\circ}360^{\circ}=16\)). Тому довжина\(\widehat{PQ}\) дорівнює 16 від окружності. \ текст {довжина}\ widehat {PQ} =16\ cdot 2\ pi (9) =3\ pi\ текст {одиниці}\).

    Приклад\(\PageIndex{4}\)

    Довжина дуги кола дорівнює\(\widehat{AB}=6\pi\) і дорівнює 14 окружності. Знайдіть радіус кола.

    Рішення

    Якщо 6\ pi дорівнює 14 окружності, то загальна окружність дорівнює\(4(6\pi )=24\pi\). Щоб знайти радіус, підключіть це до формули окружності та вирішіть для r.

    \(\begin{aligned} 24\pi =2\pi r \\ 12 \text{ units }=r \end{aligned}\)

    Приклад\(\PageIndex{5}\)

    Знайдіть міру центрального кута або\(\widehat{PQ}\).

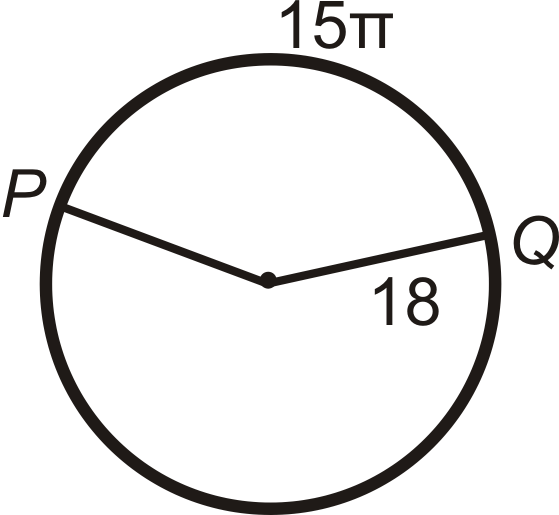
    F-д_Ф7Ф 550Е753092163ДБД 12Ф258д 89176294811ДБ29Е8Фе 01587C06255+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{5}\)

    Рішення

    Давайте підключимо те, що ми знаємо, до формули довжини дуги.

    \(\begin{aligned}15\pi &=m\widehat{PQ}360^{\circ}\cdot 2\pi (18) \\ 15&=m\widehat{PQ}10^{\circ} \\ 150^{\circ}&=m\widehat{PQ}\end{aligned}\)

    Рецензія

    Знайти довжину дуги\(\widehat{PQ}\) в\(\bigodot A\). Залиште свої відповіді з точки зору\(\pi\).

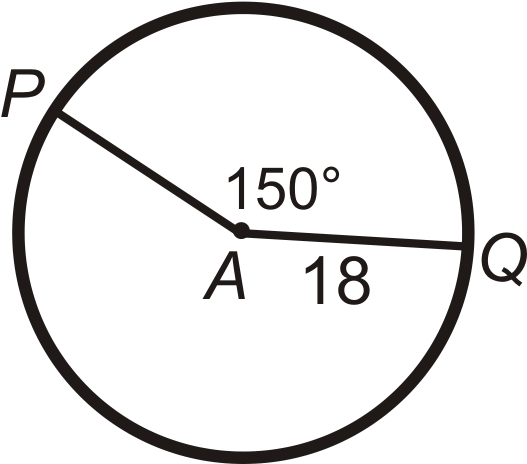
    1. F-D_F8E2369DA98B2F02CEA5D4DCFD 2D3A6A53А56ДФ 76116436FF29BC668+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{6}\)
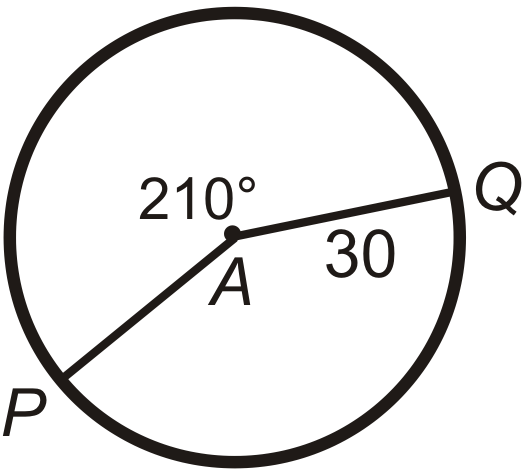
    2. F-D_2D2C11149120225E0F61C939d2A76 ДБ87Ф9121748715 ДФ2Б2Б010ДА+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
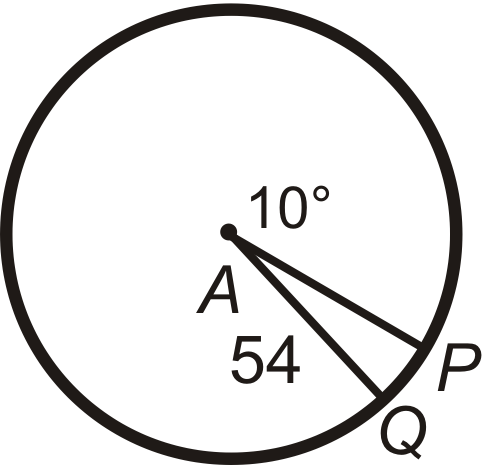
    3. F-д_7ЕФ9Ф9Д 66Е120А2С8КС8АА3Ф946АЦ5Е747Ф9ЕД671 Б2С5Е40Б16Д+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
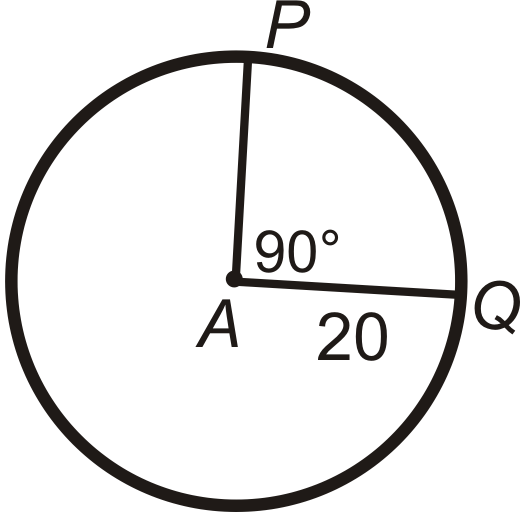
    4. F-D_851093 Ліжко Ф6261 ФК1 CF7387БФ 78А601С05Д364Е1С9051839 АФБ8ЕС86+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)

    Знайти\(PA\) (радіус) в\(\bigodot A\). Залиште свою відповідь з точки зору\(\pi \).

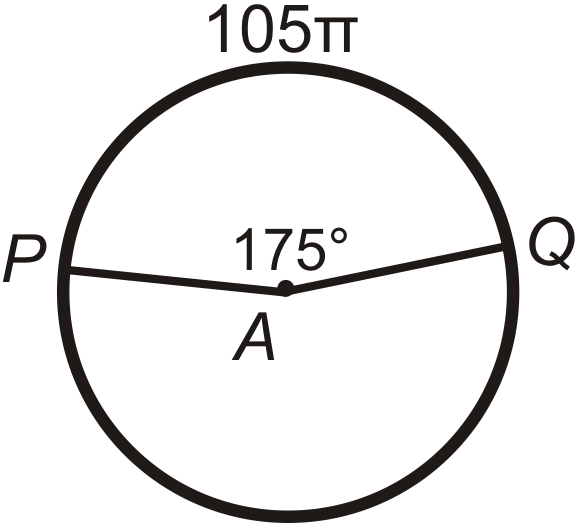
    1. F-D_EB6382519 ФЕ392222Е48ЕД 48ЕД 7678 А5Е8Д6С5Е53А8016ДД929А1А+зображення_крихіткий+зображення_крихітне зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
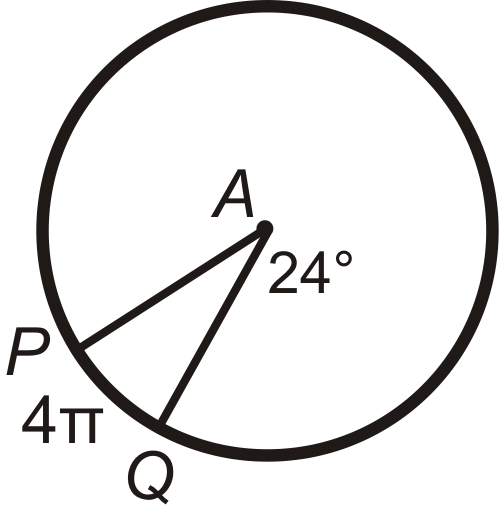
    2. F-д_7БА 6169Д8 АБ9А1АФ 209 Е67635379 ББ4А4А4С2ЕС0А97ЕФ1566511Е868Б8+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
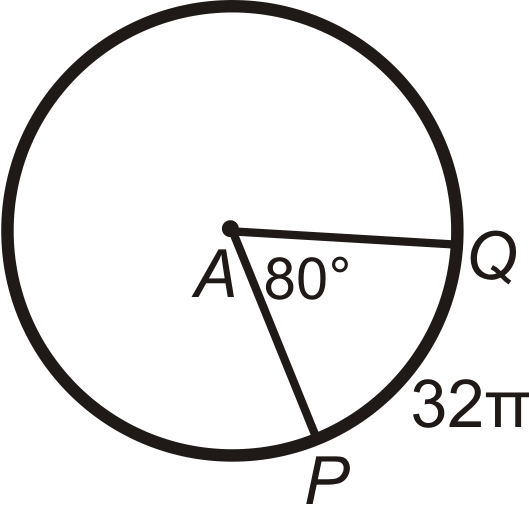
    3. Ф-д_С15Ф51Д9654БДА8Е2С11СА2БФЦ 63 Дед 978Е800к30дББ0716Ф26ЕБ57Е+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)

    Знайдіть центральний кут або\(m\widehat{PQ}\) в\(\bigodot A\). Округляйте будь-які десяткові відповіді до найближчої десятої.

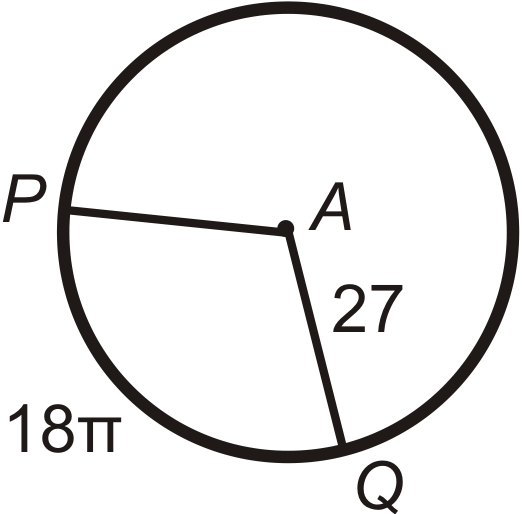
    1. F-д_41954Б765Ф39Ф 9695 ЕБ64Д3Е209Д6Ф56Д7Е874А56к593Д8Б7Е679380+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
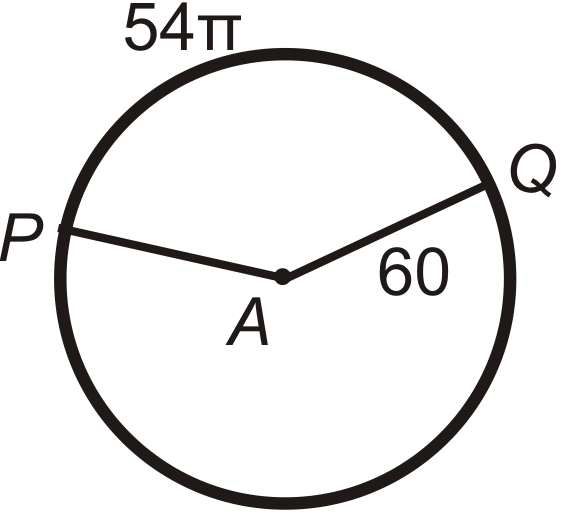
    2. F-д_63 А1749С641Ф3726ФЦ81120 ЕС7Б931665КС3Б4 ДБ798985ФФ 81C4E+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
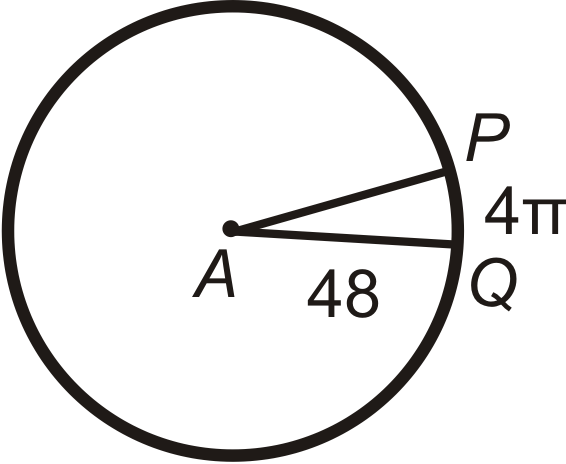
    3. F-D_AC157A3 АБФ 80000791590Ф9Ф9ДБ9ДБ9ДБ9Д2Д456А94490384Ф1Е22БК65Е3+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.9.

    Лексика

    Термін Визначення
    акорд Відрізок лінії, кінцеві точки якого знаходяться на колі.
    коло Сукупність всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    пі (Або\(\pi\)) Відношення окружності кола до його діаметру.
    радіус Відстань від центру до зовнішнього обідка кола.
    Дуга Дуга - це ділянка окружності кола.
    довжина дуги У обчисленні довжина дуги - це довжина кривої площини функції протягом інтервалу.
    Окружність Окружність кола - це міра відстані навколо зовнішнього краю кола.
    Дилатація Зменшити або збільшити цифру відповідно до масштабного коефіцієнта - це розширення.
    радіан Радіан - це одиниця кута, яка дорівнює куту, створеному в центрі кола, дуга якого по довжині дорівнює радіусу.
    Сектор Сектор кола - це частина кола, що міститься між двома радіусами кола. Сектори можна вимірювати в градусах.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи довжини дуги - основні

    Діяльність: Питання обговорення довжини дуги

    Навчальні посібники: Посібник з вивчення довжини кола та дуги

    Практика: Довжина дуги

    Реальний світ: як далеко до Лондона?