6.10: Площа секторів і сегментів

Площа частин кола.

Площа секторів і сегментів

Сектор кола - це область, обмежена двома радіусами і дугою між кінцевими точками радіусів. Якщо r - радіус, а\ widehat {AB} - дуга, що обмежує сектор, то площа сектора дорівнює\(A=\dfrac{m\widehat{AB} }{360^{\circ}}\cdot \pi r^2\).

Малюнок\(\PageIndex{1}\)

Відрізок кола - це площа кола, яка обмежена хордою і дугою з тими ж кінцевими точками, що і хорда. Площа відрізка дорівнює\(A_{\text{segment}}=A_sector−A_{\Delta ABC}\)

Малюнок\(\PageIndex{2}\)

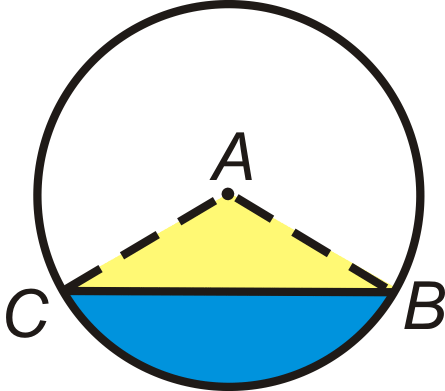
Що робити, якщо вам дали коло з двома радіусами, в якому область між цими двома радіусами була затінена? Як ви могли знайти площу цієї затіненої області кола?

Приклад\(\PageIndex{1}\)

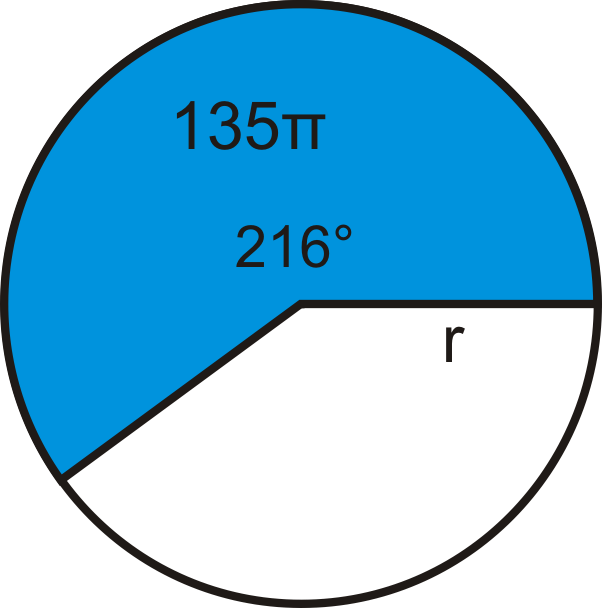
Площа сектора дорівнює,\(135 \pi\) а міра дуги дорівнює 216^ {\ circ}. Що таке радіус кола?

Малюнок\(\PageIndex{3}\)

Рішення

Підключіть те, що ви знаєте, до формули площі сектора і вирішіть для r.

\(\begin{aligned} 135 \pi &= \dfrac{216^{\circ}}{360^{\circ}}\cdot \pi r^2 \\ 135&=35\cdot r^2 \\ \dfrac{5}{3} \cdot 135 &=r^2 \\ 225 &=r^2 \rightarrow r=\sqrt{225}=15 \end{aligned}\)

Приклад\(\PageIndex{2}\)

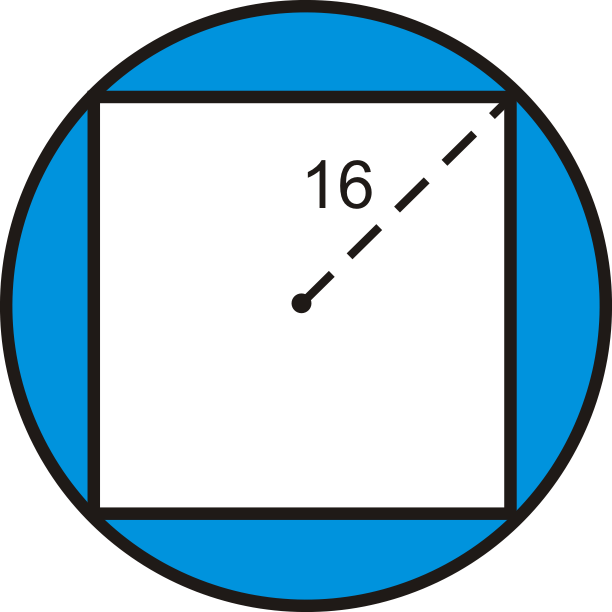
Знайдіть площу затіненої області. Чотирикутник - квадрат.

Малюнок\(\PageIndex{4}\)

Рішення

Радіус кола дорівнює 16, що також становить половину діагоналі квадрата. Отже, діагональ дорівнює 32, а сторони будуть\ dfrac {32} {\ sqrt {2}}\ cdot\ dfrac {\ sqrt {2}} {\ sqrt {2}} =16\ sqrt {2}, оскільки кожна половина квадрата є трикутником 45-45-90.

\(\begin{aligned}A_{\text{circle}}&=16^2 \pi =256 \pi \\ A_{\text{square}}&=(16\sqrt{2})^2=256\cdot 2=512 \end{aligned}\)

Площа затіненої області становить\(256 \pi −512 \approx 292.25\)

Приклад\(\PageIndex{3}\)

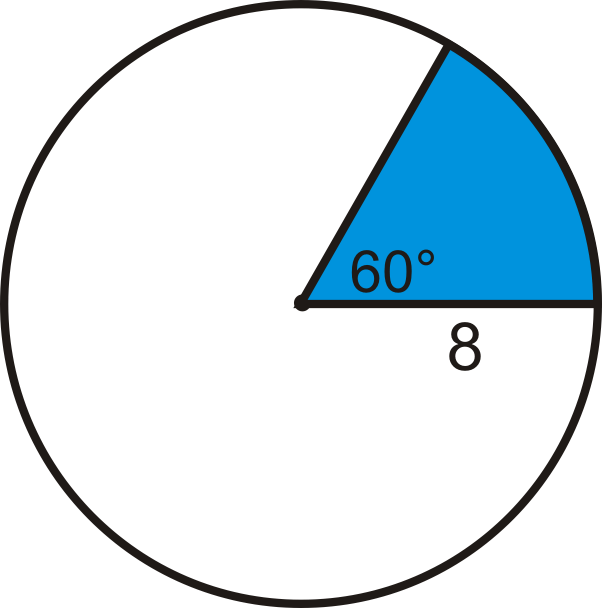
Знаходимо область синього сектора. Залиште свою відповідь з точки зору\(\pi \).

Малюнок\(\PageIndex{5}\)

Рішення

На малюнку центральний кут, який відповідає сектору\(60^{\circ}\). \(60^{\circ}\)становить 16 з\(360^{\circ}\), тому цей сектор становить 16 від загальної площі. \(\text{area of blue sector }=16\cdot \pi 8^2=\dfrac{32}{3} \pi\)

Приклад\(\PageIndex{1}\)

Площа сектора дорівнює,\(8 \pi\) а радіус кола дорівнює 12. Що таке центральний кут?

Рішення

Підключіть те, що ви знаєте, до формули площі сектора, а потім вирішіть для центрального кута, який ми будемо називати x.

Малюнок\(\PageIndex{6}\)

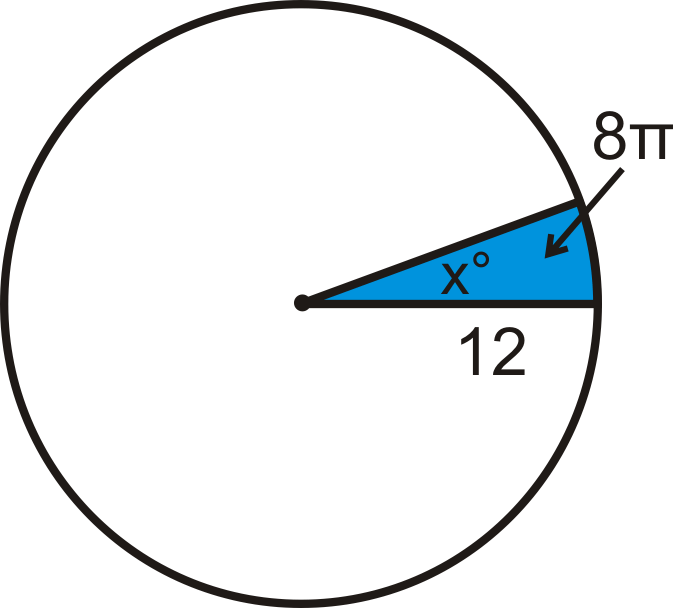
\(\begin{aligned}8 \pi &=\dfrac{x}{360^{\circ}}\cdot \pi 12^2 \\ 8 \pi &=\dfrac{x}{360^{\circ}}\cdot144 \pi \\ 8&=\dfrac{2x}{5^{\circ}} \\ x&=8\cdot \dfrac{5^{\circ}}{2}=20^{\circ} \end{aligned}\)

Приклад\(\PageIndex{1}\)

Знайдіть область синього відрізка нижче.

Малюнок\(\PageIndex{7}\)

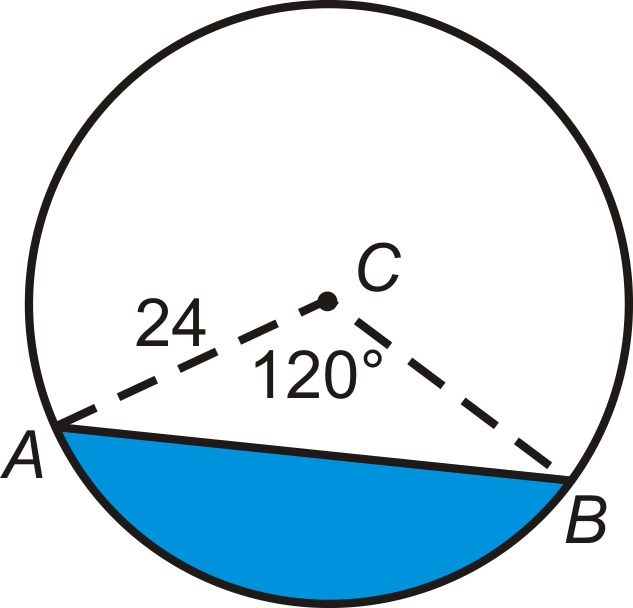
Рішення

Площа відрізка - площа сектора мінус площа рівнобедреного трикутника, зроблена радіусами. Якщо розділити рівнобедрений трикутник навпіл, то кожна половина - трикутник 30-60-90, де радіус - гіпотенуза. Висота\ DeltaABC дорівнює 12, а основа - 2 (123—√) = 243—√.

\ (\ почати {масив} {rlrl}
A_ {\ текст {сектор}} & =\ frac {120} {360}\ пі\ cdot 24^ {2} & A_ {\ трикутник} & =\ frac {1} {2} (24\ sqrt {3}) (12)\\
& =192\ pi & & = 144\ sqrt {3}
\ кінець {масив})

Площа відрізка дорівнює\(A=192\pi−144\sqrt{3}\approx 353.8 \text{ units}\).

Рецензія

Знайдіть область синього сектора або відрізка в A, залиште свої відповіді в терміні\ pi. Округляйте будь-які десяткові відповіді до найближчих сотих.

1. 
   

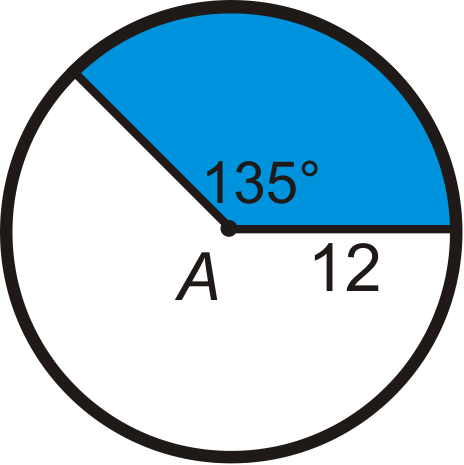
   Малюнок\(\PageIndex{8}\)

2. 

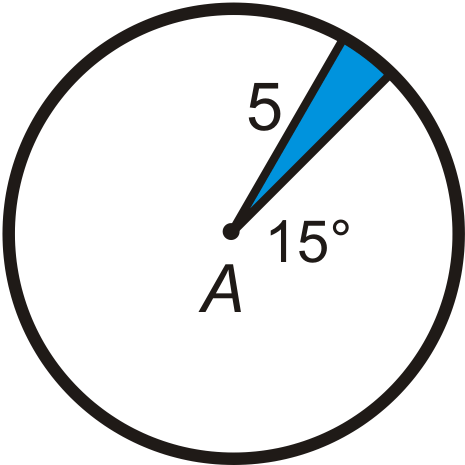
   Малюнок\(\PageIndex{9}\)

3. 

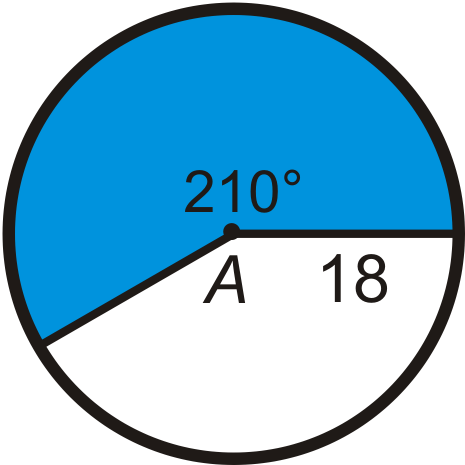
   Малюнок\(\PageIndex{10}\)

4. 

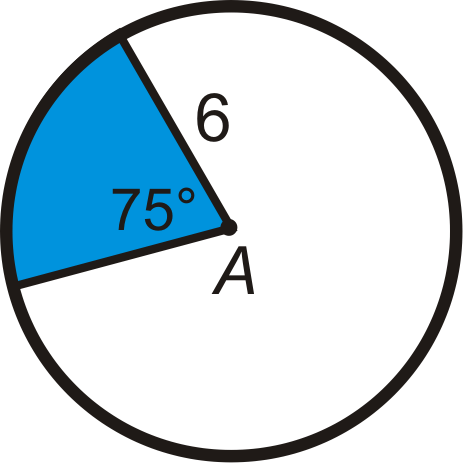
   Малюнок\(\PageIndex{11}\)

5. 

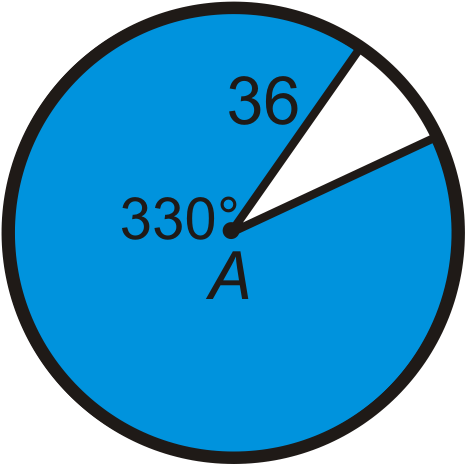
   Малюнок\(\PageIndex{12}\)

Знайдіть радіус кола. Залиште свою відповідь з точки зору\ pi.

6. 
   

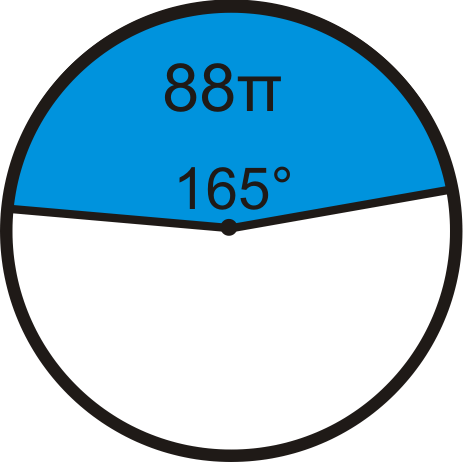
   Малюнок\(\PageIndex{13}\)

7. 

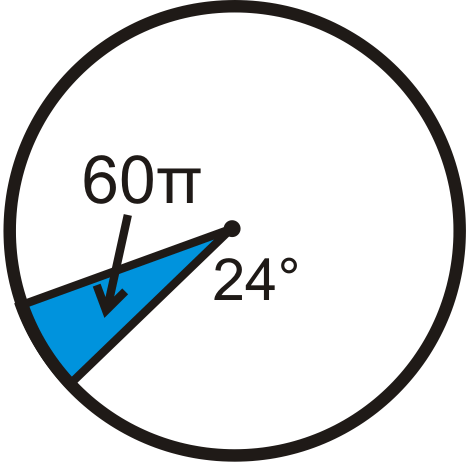
   Малюнок\(\PageIndex{14}\)

8. 

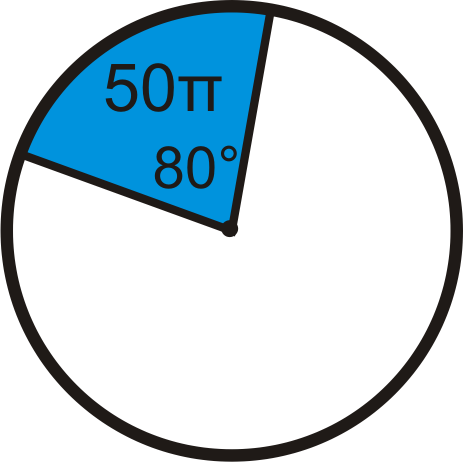
   Малюнок\(\PageIndex{15}\)

Знайдіть центральний кут кожного синього сектора. Округляйте будь-які десяткові відповіді до найближчої десятої.

9. 
   

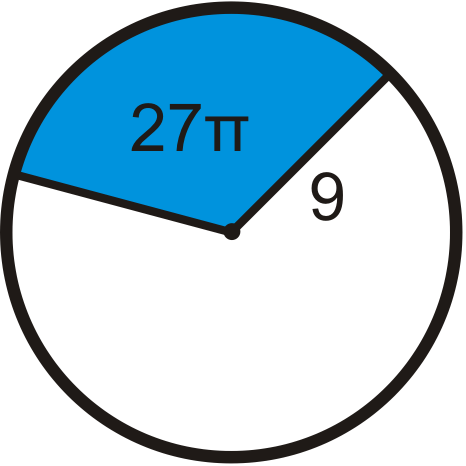
   Малюнок\(\PageIndex{16}\)

10. 

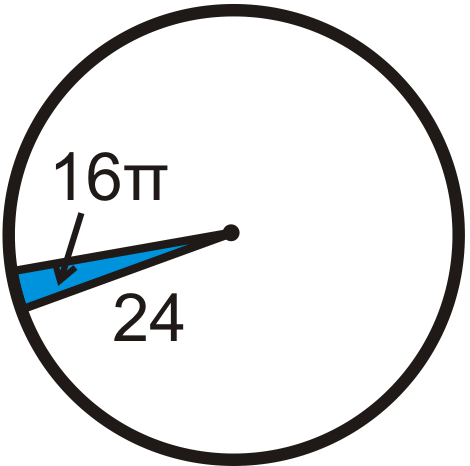
    Малюнок\(\PageIndex{17}\)

11. 

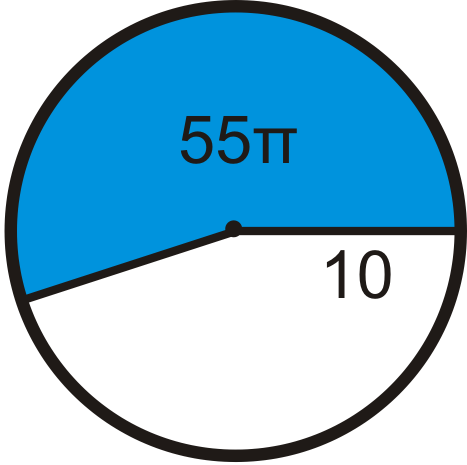
    Малюнок\(\PageIndex{18}\)

12. Знайдіть площу сектора в A, залиште свою відповідь у терміні\ pi.

    

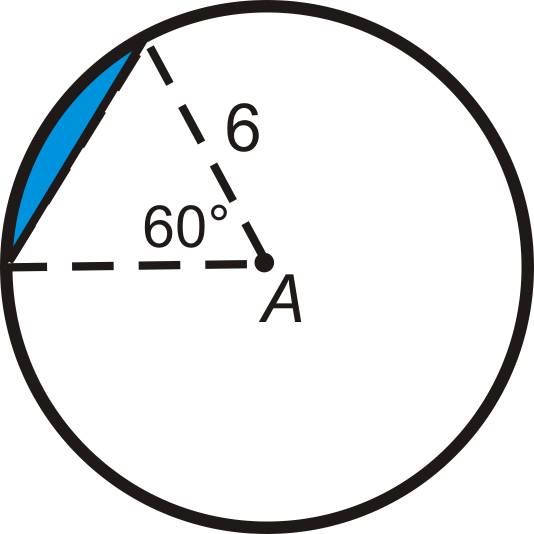
    Малюнок\(\PageIndex{19}\)

13. Знайти площу рівностороннього трикутника.
14. Знайдіть площу відрізка. Округлите відповідь до найближчої сотої.
15. Знайдіть площу сектора в A, залиште свою відповідь у терміні\ pi.
16. Знайдіть площу прямокутного трикутника.

    

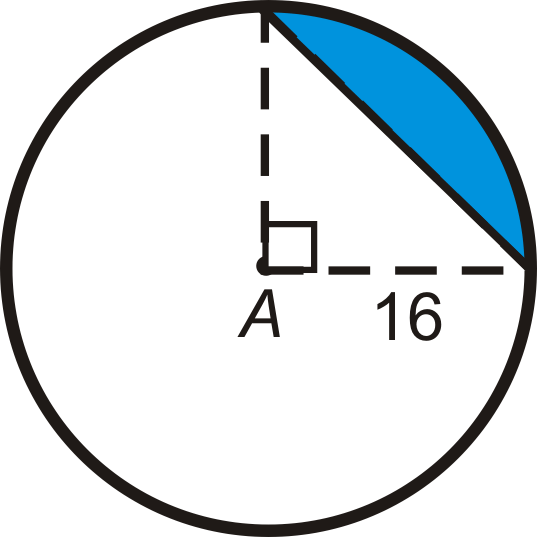
    Малюнок\(\PageIndex{20}\)

17. Знайдіть площу відрізка. Округлите відповідь до найближчої сотої.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 10.11.

Лексика

Термін	Визначення
акорд	Відрізок лінії, кінцеві точки якого знаходяться на колі.
коло	Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
діаметр	Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
пі	(Або\ pi) Відношення окружності кола до його діаметру.
радіус	Відстань від центру до зовнішнього обідка кола.
Дуга	Дуга - це ділянка окружності кола.
довжина дуги	У обчисленні довжина дуги - це довжина кривої площини функції протягом інтервалу.
радіан	Радіан - це одиниця кута, яка дорівнює куту, створеному в центрі кола, дуга якого по довжині дорівнює радіусу.
Коефіцієнт масштабування	Масштабний коефіцієнт - це відношення масштабу до вихідного або фактичного виміру, написаного в найпростішій формі.
Сектор	Сектор кола - це частина кола, що міститься між двома радіусами кола. Сектори можна вимірювати в градусах.
Сектор кола	Сектор кола - це область, обмежена двома радіусами і дугою між кінцевими точками радіусів.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи галузі секторів та сегментів - Основні

Діяльність: Сфера секторів та сегментів Питання обговорення

Навчальні посібники: Посібник з вивчення довжини кола та дуги

Практика: Область секторів і сегментів

Реальний світ: стежте за погодою!