Skip to main content
LibreTexts - Ukrayinska

6.7: Області комбінованих фігур за участю півкіл

  1. Last updated
  2. Save as PDF
  • Page ID
    54469

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Обчислити площі неправильної форми.

    Області об'єднаних фігур за участю кіл

    F-D_3ЕЕ70037 Додати B124BFB68C6F8C4C375E90117F976CC645E2863BB4B4C+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{1}\)

    Велика частина відкритого баскетбольного майданчика вже була перефарбована в зелений колір. Єдина частина, яку залишилося повторити, була коричнева клавіша. Малярам необхідно знати загальну площу простору, що залишився, щоб придбати достатню кількість фарби. З огляду на наведені нижче розміри, яку площу повинні використовувати працівники для розрахунку своїх поставок?

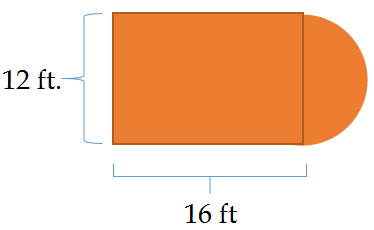
    F-D_6589129941d948e6263403850f46e82834БК2E15CFA406F6780A77A+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{2}\)

    У цій концепції ви дізнаєтеся, як знайти площу складових фігур, що містять кола.

    Знаходження площі композитних фігур

    Формула для пошуку площі прямокутника є\(A=lw\). Формула, щоб знайти площу кола є\(A=\pi r^2\). Щоб знайти площу складеної фігури, просто знайдіть площу кожної окремої фігури та додайте їх разом. Порядок, в якому ви обчислюєте площі, не має значення, і комутативна власність стверджує, що не має значення, в якому порядку ви їх додаєте.

    Давайте розглянемо приклад.

    Знайдіть площу малюнка нижче.

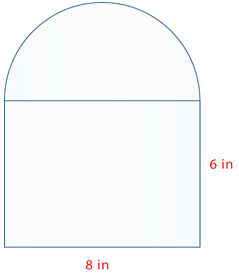
    F-D_834B50506D2C8C4D3D 68F57437E3B0E7A7DC FAE71CCB3FE8E39694+зображення_thumb_поштова листівка_крихіткий+зображення_thumb_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{3}\)

    Спочатку знайдіть площу прямокутника.

    \(\begin{aligned} A&=lw \\ A&=6(8) \\ A&=48\end{aligned}\)

    Площа прямокутника становить 48 квадратних дюймів.

    Далі, визнайте, що вам дали діаметр і потрібно розділити це на 2, щоб отримати радіус.

    \(\begin{aligned} A&=\pi r^2 \\ A&=3.14(4)^{2} \\ A&=3.14(16) \\ A&=50.24\text{ sq. in. } \end{aligned}\)

    Площа повного кола становить 50,24 квадратних дюймів.

    Потім знайдіть площу однієї половини кола, півкола, розділивши свою остаточну відповідь на 2.

    \(A=25.12\)

    Площа півкола дорівнює 25,12 квадратних дюймів.

    Нарешті, додайте дві області разом.

    \(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=48+25.12 \\ A&=73.12\text{ sq. in. } \end{aligned}\)

    Відповідь - складена фігура має площу 73,12 квадратних дюйма.

    Приклад\(\PageIndex{1}\)

    Раніше вам давали проблему з приводу відкритого баскетбольного майданчика, який потребує деякої фарби.

    Працівники мали такі розміри суду і повинні знати загальну площу, щоб з'ясувати свої поставки.

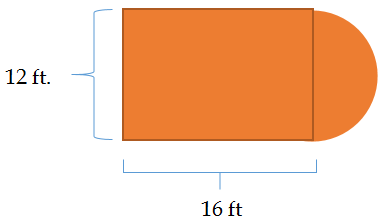
    F-D_8946AF2DCE7794B99116255D1E3cd544ad6199349F2925DAA875A2C+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{4}\)

    Рішення

    Спочатку знайдіть площу прямокутника.

    \(\begin{aligned}A&=lw \\ A&=16(12) \\ A&=192\end{aligned}\)

    Площа прямокутника становить 192 квадратних футів.

    Далі, визнайте, що вам дали діаметр і потрібно розділити це на 2, щоб отримати радіус. У задачі зазначено, що діаметр кола такий же, як ширина прямокутника, 3 фути.

    \(\begin{aligned} A&=\pi r^2 \\ A&=3.14(6)^{2} \\ A&=3.14(36) \\ A&=113.04\end{aligned}\)

    Площа для повного кола становить приблизно 113 квадратних футів.

    Потім пам'ятайте, що у вас є півколо і розділіть цю область на 2.

    \(A_{sc}=56.5\)

    Площа півкола становить 56,5 квадратних футів.

    Додайте дві області разом.

    \(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=192+56.5 \\ A&=248.5\text{ sq. ft. }\end{aligned}\)

    Відповідь полягає в тому, що складена фігура має область\(A=248.5\text{ square feet }\). Працівникам потрібно буде придбати достатню кількість фарби, щоб покрити 248,5 кв. футів.

    Приклад\(\PageIndex{2}\)

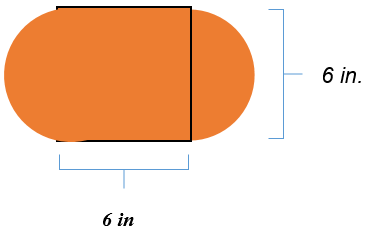
    На малюнку нижче два півкола з квадратом посередині. Квадрат має довжину сторони 6 дюймів.

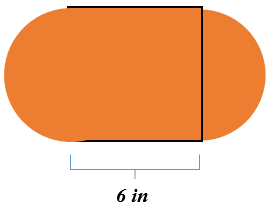
    F-D_C0CB792 CEECF27510DF5B5D31B57E825A138597A30F983626E4DEC+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{5}\)

    Рішення

    Далі визначаємо площу квадрата.

    \(\begin{aligned} A&=s^2 \\ A&=6^2 \\ A&=36\end{aligned}\)

    Площа квадрата становить 36 квадратних дюймів.

    Потім визнайте, що оскільки квадрат має чотири рівні сторони, діаметр кола також становить 6 дюймів.

    F-D_07134791e023f625068F4993853d3D3d76B451EE4B79489f0d959af510+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{6}\)

    Формула площі одного півкола - це формула площі кола, поділеної на 2.

    \(A_{sc}=\dfrac{\pi r^2}{2}\)

    Оскільки є два півкола однакового розміру, ви можете просто скласти їх разом, щоб в кінцевому підсумку отримати область для повного кола.

    Пам'ятайте, що вам дали діаметр, а не радіус, тому розділіть діаметр на 2.

    Потім скористайтеся формулою для площі кола.

    \(\begin{aligned} A&=\pi r^2 \\ A&=3.14(3)^{2} \\ A&=3.14(9) \\ A&=28.26\end{aligned}\)

    Площа двох півкіл, які утворюють одне повне коло, становить 28,26 квадратних дюймів.

    Нарешті, додайте дві області разом.

    \(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=36+28.26 \\ A&=64.26\end{aligned}\)

    Відповідь полягає в тому, що складена фігура має область\(A=64.26\text{ square inches }\)

    Приклад\(\PageIndex{3}\)

    Знайдіть складену площу прямокутника довжиною 5 футів і шириною 3 фути, з'єднану з півколом з тим же діаметром, що і ширина.

    Рішення

    Спочатку знайдіть площу прямокутника.

    \(\begin{aligned} A&=lw \\ A&=5(3) \\ A&=15\end{aligned}\)

    Площа прямокутника становить 15 квадратних футів.

    Далі, визнайте, що вам дали діаметр і потрібно розділити це на 2, щоб отримати радіус. У задачі зазначено, що діаметр кола такий же, як ширина прямокутника, 3 фути.

    \(\begin{aligned} A&=\pi r^2 \\ A&=3.14(1.5)^{2} \\ A&=3.14(2.25) \\ A&=7.065\end{aligned}\)

    Площа для повного кола становить 7.065 квадратних футів.

    Потім пам'ятайте, що у вас є півколо і розділіть цю область на 2.

    \(A_{sc}=3.53\)

    Площа півкола становить 3,53 квадратних футів.

    Додайте дві області разом.

    \(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=15+3.53 \\ A&=18.53\text{ sq. ft. }.\end{aligned}\)

    Відповідь полягає в тому, що складена фігура має область\(A=18.53 \text{ square feet }\).

    Приклад\(\PageIndex{4}\)

    Знайдіть складену площу квадрата з довжиною сторони 4 мм і півкола діаметром тієї ж довжини сторони, що і квадрат.

    Рішення

    Спочатку знайдіть площу квадрата.

    \(\begin{aligned} A&=s^2 \\ A&=4^2 \\ A&=16 \end{aligned}\)

    Площа квадрата становить 16 квадратних міліметрів.

    Далі, визнайте, що вам дали діаметр і потрібно розділити це на 2, щоб отримати радіус. У задачі зазначено, що діаметр кола такий же, як довжина сторони квадрата, 4 мм.

    \(\begin{aligned} A&=\pi r^2 \\ A&=3.14(2)^{2} \\ A&=3.14(4) \\ A&=12.56\end{aligned}\)

    Площа для повного кола становить 12,56 квадратних міліметрів.

    Потім пам'ятайте, що у вас є півколо і розділіть цю область на 2.

    \(A_{sc}=6.28\)

    Площа півкола становить 6,28 квадратних міліметрів.

    Додайте дві області разом.

    \(\begin{aligned} A&=AS+A_{sc} \\ A&=16+6.28 \\ A&=22.28\text{ sq. mm. }\end{aligned}\)

    Відповідь полягає в тому, що складена фігура має область\(A=22.28\text{ sq. mm. }\)

    Приклад\(\PageIndex{5}\)

    Знайдіть площу фігури, яка складається з квадрата і півкола. Квадрат має довжину сторони 8 дюймів. Діаметр кола такий же, як довжина сторони квадрата.

    Рішення

    Спочатку знайдіть площу квадрата.

    \(\begin{aligned} A&=s^2 \\ A&=8^2 \\ A&=64\end{aligned} \)

    Площа квадрата становить 64 квадратних дюйма.

    Далі, визнайте, що вам дали діаметр і потрібно розділити це на 2, щоб отримати радіус. Проблема стверджує, що діаметр кола такий же, як довжина сторони квадрата, 8 дюймів.

    \(\begin{aligned} A&=\pi r^2 \\ A&=3.14(4)^{2} \\ A&=3.14(16) \\ A&=50.24 \end{aligned}\)

    Площа для повного кола становить 50,24 квадратних дюймів.

    Потім пам'ятайте, що у вас є півколо і розділіть цю область на 2.

    \(A_{sc}=25.12\)

    Площа півкола дорівнює 25,12 квадратних дюймів.

    Додайте дві області разом.

    \(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=64+25.12 \\ A&=79.12\text{ square inches } \end{aligned}\)

    Відповідь полягає в тому, що складена фігура має область\(A=79.12\text{ sq. in. }\)

    Рецензія

    Знайдіть площу кожної об'єднаної фігури.

    1. Квадрат і півколо. Квадрат має довжину сторони 11 мм. Діаметр кола збігається зі стороною квадрата.
    2. Квадрат і півколо. Квадрат має довжину сторони 8,5 дюймів. Діаметр кола збігається зі стороною квадрата.
    3. Квадрат і півколо. Квадрат має довжину сторони 7,25 дюйма. Діаметр кола збігається зі стороною квадрата.
    4. Квадрат і півколо. Квадрат має довжину сторони 13 футів. Діаметр кола збігається зі стороною квадрата.
    5. Квадрат і півколо. Квадрат має довжину сторони 15.5 футів. Діаметр кола збігається зі стороною квадрата.
    6. Прямокутник і півколо. Прямокутник має довжину 8 футів і ширину 5 футів. Діаметр кола відповідає ширині.
    7. Прямокутник і півколо. Прямокутник має довжину 8,5 футів і ширину 6 футів. Діаметр кола відповідає ширині.
    8. Прямокутник і півколо. Прямокутник має довжину 9 дюймів і ширину 4,5 дюйма. Діаметр кола відповідає довжині.
    9. Прямокутник і півколо. Прямокутник має довжину 7 футів і ширину 4 фути. Діаметр кола відповідає довжині.
    10. Прямокутник і півколо. Прямокутник має довжину 5,5 футів і ширину 3.5 футів. Діаметр кола відповідає ширині.
    11. Трикутник і півколо. Трикутник має основу 5 дюймів і висоту 4 дюйми. Діаметр кола збігається з основою трикутника.
    12. Трикутник і півколо. Трикутник має основу 7 дюймів і висоту 6 дюймів. Діаметр кола збігається з основою трикутника.
    13. Трикутник і півколо. Трикутник має основу 5,5 дюймів і висоту 4 дюйми. Діаметр кола збігається з основою трикутника.

    Вирішіть кожну проблему.

    1. Роб малює великі горошок на аркуші на тлі шкільного мюзиклу. Він намалював 16 горошок, кожна радіусом 3 фути. Яку загальну площу покривають горошок?
    2. Бібліотекар має бібліотеку в своїй школі килимом. Бібліотека являє собою круглий зал діаметром 420 футів. Скільки квадратних футів килима їй потрібно буде замовити?

    Ресурси

    Лексика

    Термін Визначення
    Площа Площа - простір в межах периметра двомірної фігури.
    Коло Коло - це сукупність всіх точок на певній відстані від заданої точки в двох вимірах.
    Діаметр Діаметр - це міра відстані через центр кола. Діаметр дорівнює подвоєної мірі радіуса.

    Додаткові ресурси

    Відео: Площа і периметр

    Практика: Області комбінованих фігур із залученням півкіл

    Реальний світ: Стрільба кіл