Skip to main content
LibreTexts - Ukrayinska

6.6: Площа кола

  1. Last updated
  2. Save as PDF
  • Page ID
    54461

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Площа кола

    Щоб знайти площу кола, все, що вам потрібно знати, це його радіус. Якщо r - радіус кола, то його площа дорівнює\(A=\pi r^2\).

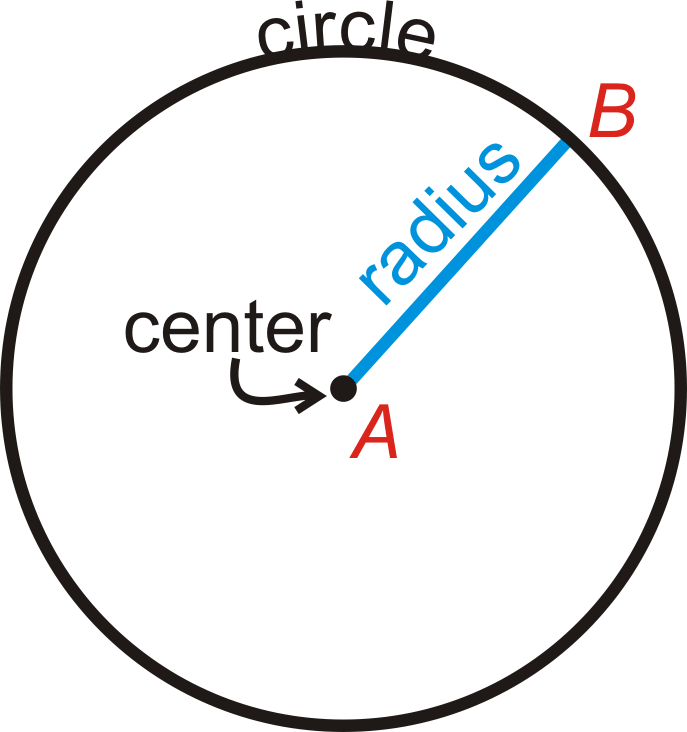
    Ф-Д_234Е9 КС5Ф3ААА0СА982Д5ФБ5ДБ5ДБ075217С3БК 5093884 БК 6КК41ФА+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Ми залишимо свої відповіді в терміні\(\pi\), якщо не вказано інше.

    Що робити, якщо вам дали радіус або діаметр кола? Як ви могли знайти кількість місця, яке займає коло?

    Приклад\(\PageIndex{1}\)

    Знайдіть площу кола діаметром 12 см.

    Рішення

    Якщо\(d=12\text{ cm }\), то\(r=6\text{ cm }\). Площа є\(A=\pi (6^2)=36\pi \text{ cm }^2\).

    Приклад\(\PageIndex{2}\)

    Якщо площа кола є\(20\pi \text{ units }\), який радіус?

    Рішення

    Підключіть область і вирішіть для радіуса.

    \(\begin{aligned} 20\pi &=\pi r^2 \\ 20&=r^2 \\ r&=\sqrt{20}=2\sqrt{5}\text{ units } \end{aligned}\)

    Приклад\(\PageIndex{3}\)

    Коло вписується в квадрат. Кожна сторона квадрата довжиною 10 см. Яка площа кола?

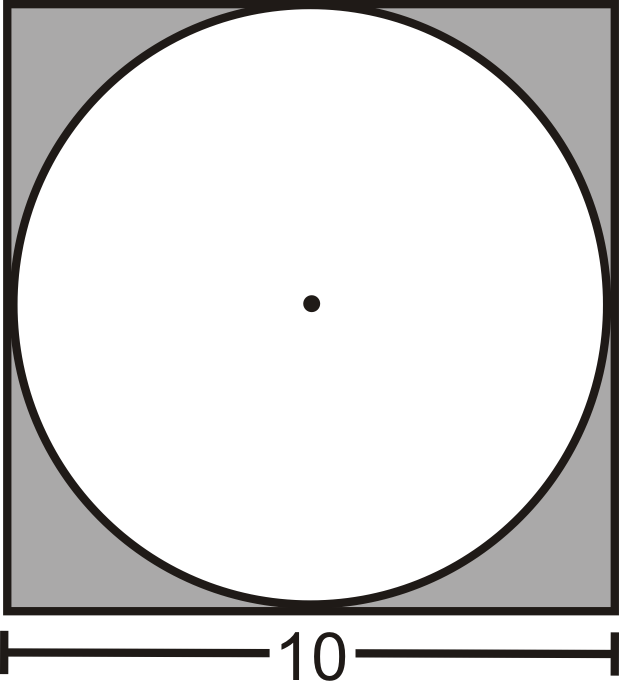
    F-D_C26733 АА6 Е50 БББ17Д9547А5Б63Б58264С222Е53 АФ 57CDC0494АФ+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Діаметр кола такий же, як довжина сторони квадрата. Тому радіус дорівнює 5 см.

    \(A=\pi 5^2=25\pi \text{ cm }^2\)

    Приклад\(\PageIndex{4}\)

    Знайдіть площу затіненої області з Прикладу 3.

    Рішення

    Площа затіненої області буде площею квадрата мінус площа кола.

    \(A=102−25\pi =100−25\pi \approx 21.46\text{ cm }^2\)

    Приклад\(\PageIndex{5}\)

    Знайти діаметр кола з площею\(36\pi \).

    Рішення

    По-перше, використовуйте формулу для площі кола, щоб вирішити для радіуса кола.

    \(\begin{aligned}A&=\pi r^2 \\ 36\pi &=\pi r^2 \\ 36&=r^2 \\ r&=6\end{aligned}\)

    Якщо радіус дорівнює 6 одиницям, то діаметр дорівнює 12 одиницям.

    Рецензія

    Заповніть наступну таблицю. Залиште всі відповіді в плані\(\pi\).

    радіус Площа окружність
    1. 2
    2. \(16\pi\)
    3. \(10\pi\)
    4. \(24\pi\)
    5. 9
    6. \(90\pi\)
    7. \(35\pi\)
    8. \(7\pi\)
    9. 60
    10. 36

    Знайдіть площу затіненої області. Округлите свою відповідь до найближчої сотої.

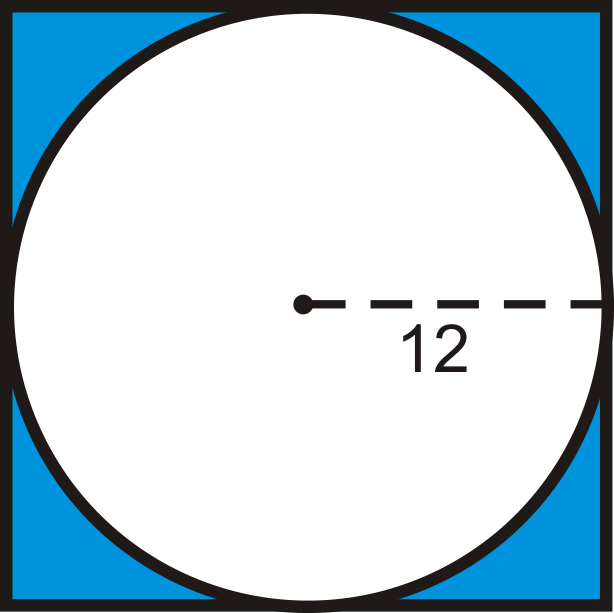
    1. F-D_6D85C3 ECE461A1A1AC5632843 ЕЦФ Ф 2DCF4D967D68CA471890E9082248+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{3}\)
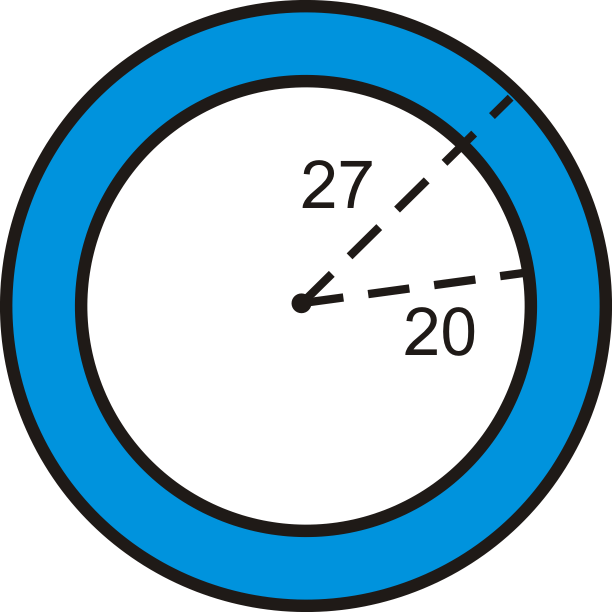
    2. F-D_3B6F51 BE8181D0779C9B529800 АБ 3D11F4DE07C97852C4E82E592A+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{4}\)
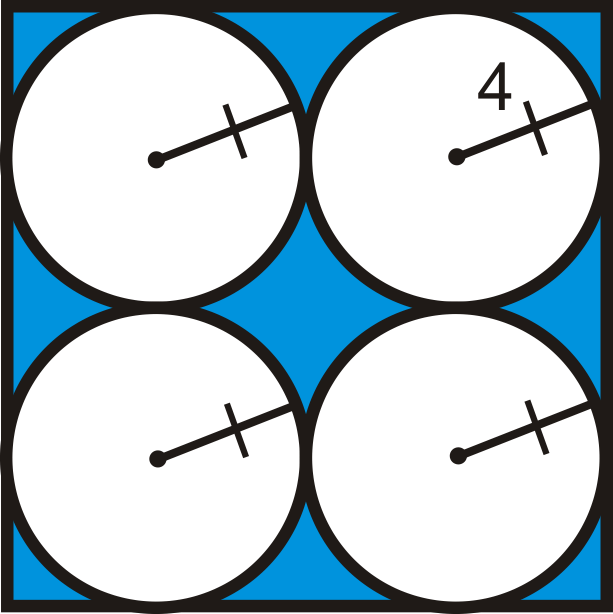
    3. F-D_C41 БД 33249E1 CFF 70119E9D капуста 75781 Е5 Е5 ЕАД 8АД 186ФБА0Ф3Б023Ф+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{5}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.10.

    Лексика

    Термін Визначення
    акорд Відрізок лінії, кінцеві точки якого знаходяться на колі.
    коло Безліч всіх точок, які знаходяться на однаковій відстані від певної точки, називається центром.
    окружність Відстань по колу.
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    пі (Або\(\pi\)) Відношення окружності кола до його діаметру.
    радіус Відстань від центру до зовнішнього обідка кола.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Визначаємо площу кола

    Види діяльності: Площа гуртка Дискусійні питання

    Навчальні посібники: Посібник з вивчення довжини кола та дуги

    Практика: Площа кола

    Реальний світ: Кільцеві сидіння