4.39: Формула відстані та алгебра

Last updated

Oct 27, 2022
Save as PDF
- 4.38: Відстань між паралельними лініями
- 4.40: Застосування формули відстані

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Використання теореми Піфагора для визначення відстаней

Припустимо, ви і ваш друг були на полювання на смітника. Починаючи з того ж місця, ви йшли 5 кварталів на схід і 3 квартали на північ. Ваш друг пройшов 7 кварталів на захід і 2 квартали на південь. Якби кожен блок був десяту частину милі завдовжки, чи могли б ви обчислити, наскільки далеко один від одного ви і ваш друг були? Як би ви це зробили?

Формула відстані

Щоб зрозуміти формулу відстані, спочатку розглянемо наступну проблему:

Знайдіть довжину відрізка, що з'єднує $(1, 5)$ і $(5, 2)$ .

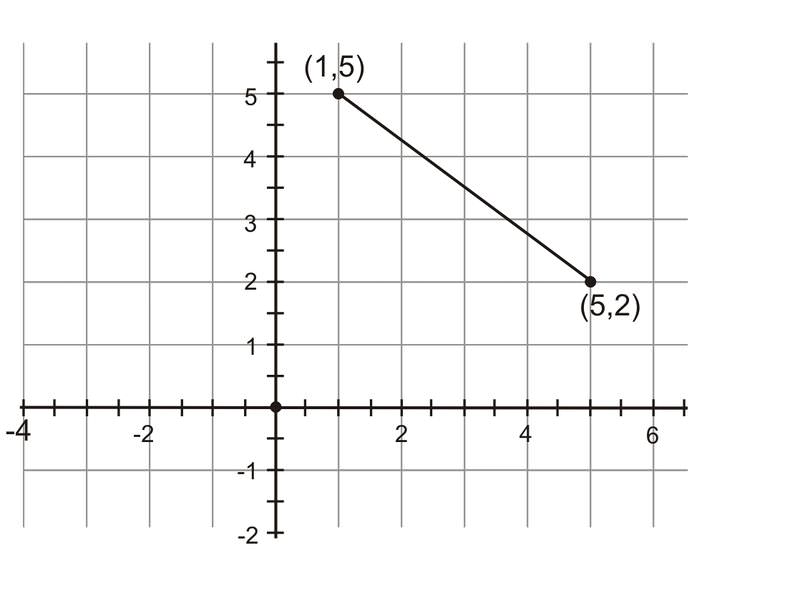
Ф-д_31д983д 3Е0А50Ф11371473913 ДБК 460Б6А3462507Е89Б3Д830АБ1+зображення_крихіткий+зображення_крихіткий.jpg — Малюнок $\PageIndex{1}$

Питання задає вам визначити довжину відрізка. Оскільки відрізок не паралельний будь-якій осі, його важко виміряти, враховуючи координатну сітку.

Однак можна вважати цей відрізок гіпотенузою прямокутного трикутника. Намалюйте вертикальну лінію і горизонтальну лінію. Знайдіть точку перетину. Ця точка представляє третю вершину в прямокутному трикутнику.

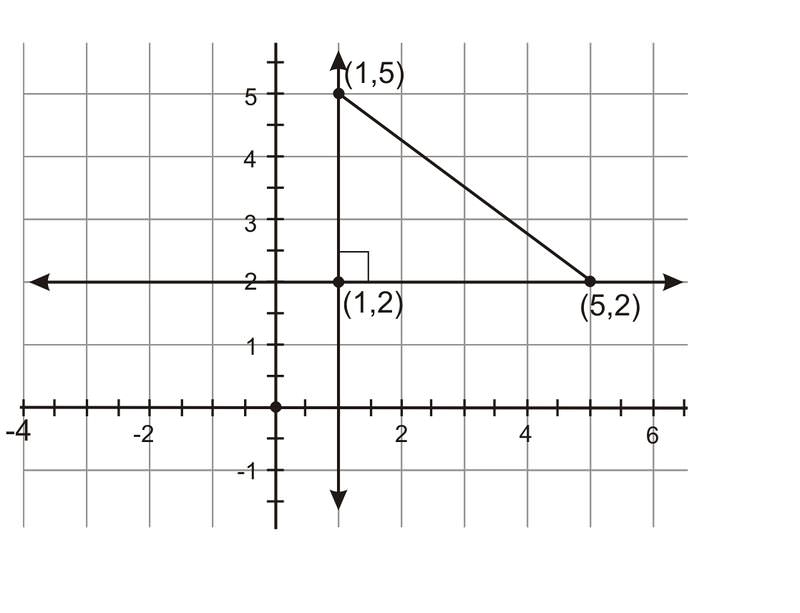
Ф-Д_63Б4ФД5647Е9Е6А3610384Ф96ФБ093988Б7Е5171548Ф465777А45519+зображення_крихіткий+зображення_крихіткий.jpg — Малюнок $\PageIndex{2}$

Можна легко порахувати довжини ніжок цього трикутника на сітці. Вертикальна ніжка тягнеться від $(1, 2)$ до $(1, 5)$ , тому вона $\mid5−2\mid=\mid3\mid=3\: units$ довга. Горизонтальна нога тягнеться від $(1, 2)$ до $(5, 2)$ , тому вона $\mid5−1\mid=\mid4\mid=4\: units$ довга. Використовуйте теорему Піфагора з цими значеннями для довжин кожного катета, щоб знайти довжину гіпотенузи.

$\begin{aligned} a^2+b^2 & =c^2 \\ 3^2+4^2 & =c^2 \\ 9+16 & =c^2 \\ 25 & =c^2 \\ \sqrt{25} & =\sqrt{c^2} \\ 5 & = c\end{aligned}$

Відрізок $(5, 2)$ з'єднує $(1, 5)$ і становить 5 одиниць довжини.

Математики спростили цей процес і створили формулу, яка використовує ці кроки для знаходження відстані між будь-якими двома точками в координатній площині. Якщо ви використовуєте формулу відстані, вам не доведеться малювати зайві лінії.

Формула відстані стверджує: Дано точки $(x_1,y_1)$ і довжина відрізка $(x_2,y_2)$ , що з'єднує ці дві точки, є $d=\sqrt{\left(y_{2}-y_{1}\right)^{2}+\left(x_{2}-x_{1}\right)^{2}}$ .

Давайте скористаємося формулою відстані для виконання наступних завдань:

Знайти відстань між $(–3, 5)$ і $(4, –2)$ .

Скористайтеся формулою відстані. Нехай $(x_1,y_1)=(−3,5)$ і $(x_2,y_2)=(4,−2)$ .

\ (\ почати {масив} {l}
d=\ sqrt {(-2-5) ^ {2} + (4- (-3)) ^ {2}}\ rightarrow\ sqrt {(-7) ^ {2} +7^ {2}}\
d=\ sqrt {98} =7\ sqrt {2}\ текст {одиниці}
\ кінець {масив}\)

О 8 ранку одного разу Амір вирішує пройтися по прямій лінії по пляжу. Після двох годин, не здійснюючи поворотів і подорожуючи з постійною швидкістю, Амір знаходився за дві милі на схід і чотири милі на північ від своєї відправної точки. Як далеко пройшов Амір і яка була його швидкість ходьби?

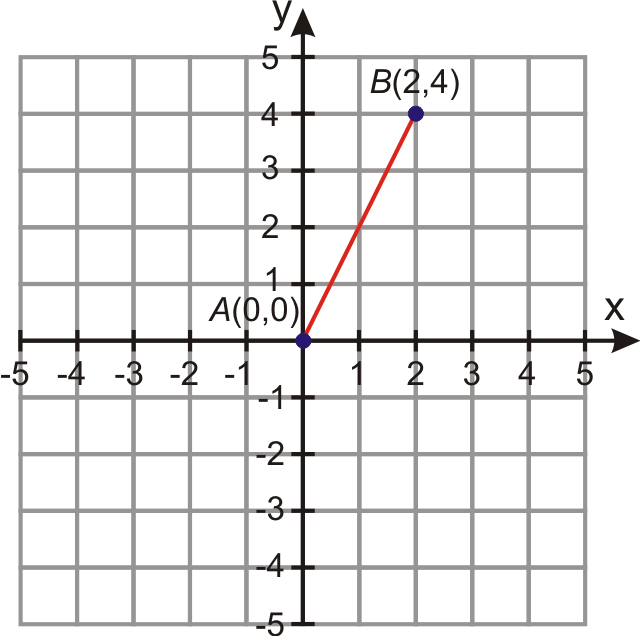
Ф-Д_ДД 78 КД017А6ДДА 9ЕЕ7837 ЕЕД А057Ф1570С565245АЕ 20599D5AD3E33C+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Покладіть маршрут Аміра на графіку координат. Ми можемо розмістити його відправну точку на початку, $A=(0,0)$ . Тоді його кінцева точка буде в точці $B=(2,4)$ . Відстань можна знайти за допомогою формули відстані.

$\begin{aligned} d&=\sqrt{(4−0)^2+(2−0)^2}=\sqrt{(4)^2+(2)^2}=\sqrt{16+4}=\sqrt{20} \\ d &=4.47\text { miles } \end{aligned}$ .

Оскільки Амір пройшов 4,47 милі за 2 години, його швидкість становить:

$Speed=\dfrac{4.47 \text{ miles }}{2 \text{ hours }}=2.24 \: mi/h$

Приклад $\PageIndex{1}$

Раніше вам сказали, що на полюванні на смітника, починаючи з того ж місця, ви йшли 5 кварталів на схід і 3 квартали на північ, а ваш друг пройшов 7 кварталів на захід і 2 квартали на південь. Кожен блок довжиною в десяту частку милі. Наскільки далеко один від одного були ви і ваш друг?

Рішення

Можливо, буде корисно намалювати графік, щоб візуалізувати ситуацію. Припускаючи, що початкова точка була в (0,0), а відстань між кожною точкою дорівнює одному блоку, якщо ви йшли 5 блоків на схід і 3 квартали на північ, ваші координати будуть $(-5, 3)$ . Ваш друг пройшов 7 кварталів на захід і 2 квартали на південь, так що їх координати будуть $(7,-2)$

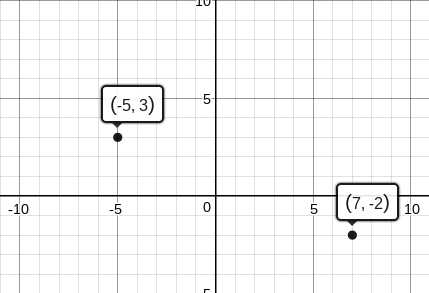
Тепер ви можете обчислити відстань між цими двома точками, використовуючи формулу відстані. Все, що вам потрібно зробити, це підключити точки до формули і вирішити.

\ (\ почати {вирівняний} d&=\ sqrt {\ ліворуч (y_ {2} -y_ {1}\ праворуч) ^ {2} +\ ліворуч (x_ {2} -x_ {1}\ праворуч) ^ {2}}\\

d&=\ sqrt {(−2−3) ^2+ (7− (−5)) ^2}\ стрілка вправо\ sqrt {(−5) ^2+12^2}\\

d&=\ sqrt {169} =13\ кінець {вирівняний}\)

Ви і ваш друг знаходяться на відстані 13 одиниць один від одного. Оскільки кожен блок становить десяту частину милі довжини, ви можете помножити 13 на одну десяту, щоб отримати фактичну відстань.

$13 \times \dfrac{1}{10}=\dfrac{13}{10}=1.3$

Ви і ваш друг знаходяться в 2,1 милі один від одного.

Приклад $\PageIndex{2}$

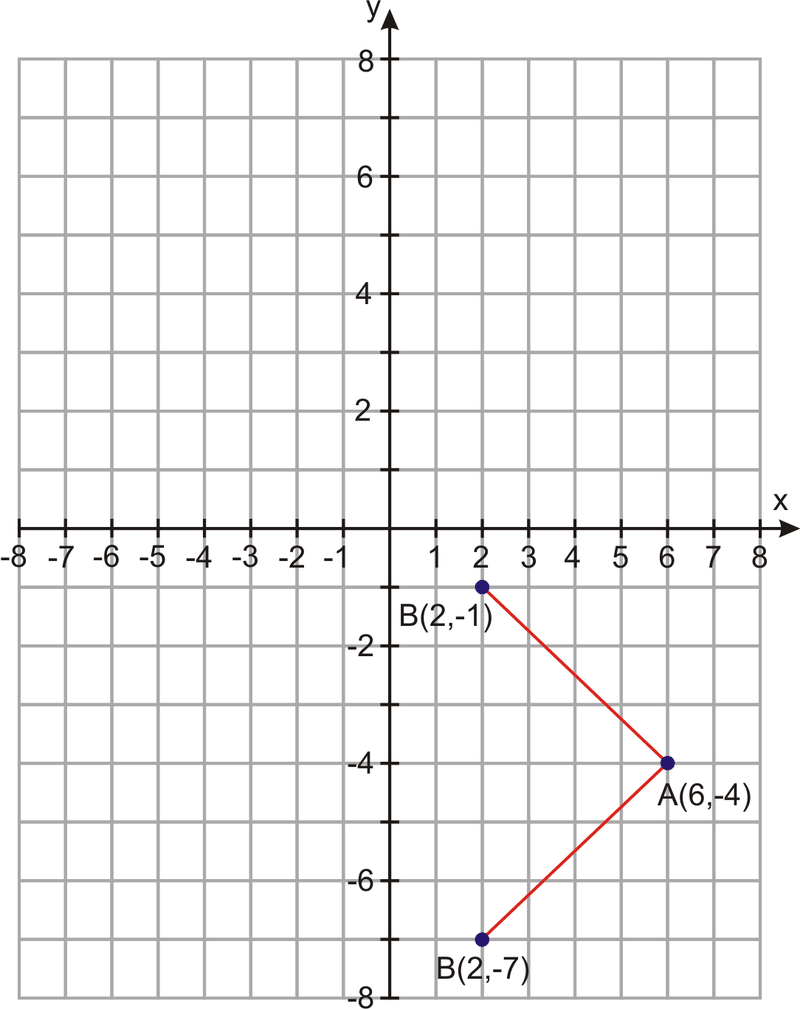
Точка $A=(6,−4)$ і точка $B=(2,k)$ . Яке значення $k$ таке, що відстань між двома точками дорівнює 5?

Рішення

Скористайтеся формулою відстані.

$d=\sqrt{(y_1−y_2)^2+(x_1−x_2)^2}\Rightarrow 5=\sqrt{(4−k)^2+(6−2)^2}$

\ (\ begin {вирівняний} Квадрат\: обидві\ :сторони\ :of\ :рівняння. &\ qquad& 5^2&= [\ sqrt {(4−k) ^2+ (6−2) ^2}] ^2\

Спростити. &\ qquad& 25&= (−4−k) ^2+16\\ Вилучити\: дужки\:. &\ qquad& 0&= k ^ 2+8к+16−9\\

Спростити. &\ qquad& 0&= к ^ 2+8к+7\\

Знайти\ :k\ :використовуючи\ :квадратичну\ :формулу. &\ qquad& k&=\ dfrac {−8\ пм\ sqrt {64−28}} {2} =\ dfrac {−8\ pm\ sqrt {36}} {2} =\ dfrac {−8\ pm6} {2}\ кінець {вирівняний}\)

$k=−7$ або $k=−1$ . Існує дві можливості для значення k. Давайте графуємо точки, щоб отримати наочне уявлення про наші результати.

F-D_655c94B9E01C99957C24БА 2634Е 608Ф0Ф5609Ф1Ф8Ф8Ф1Ф843271ADF4609AA+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{5}$

Рецензія

У 1—10 знайдіть відстань між двома точками.

$(x_1,y_1)$ і $(x_2,y_2)$
$(7, 7)$ і $(–7, 7)$
$(–3, 6)$ і $(3, –6)$
$(–3, –1)$ і $(–5, –8)$
$(3, –4)$ і $(6, 0)$
$(–1, 0)$ і $(4, 2)$
$(–3, 2)$ і $(6, 2)$
$(0.5, –2.5)$ і $(4, –4)$
$(12, –10)$ і $(0, –6)$
$(2.3, 4.5)$ і $(–3.4, –5.2)$

Знайти всі точки, що мають координату x -4 і відстань від точки $(4, 2)$ 10.
Знайти всі точки, які мають y-координату 3 і відстань $(–2, 5)$ від точки 8.
Мішель вирішує одного разу покататися на своєму велосипеді. Спочатку вона їде на своєму велосипеді через південь на 12 миль, а потім напрямок велосипедної стежки змінюється, і вона їде в новому напрямку на деякий час довше. Коли вона зупиняється, Мішель знаходиться в 2 милі на південь і в 10 милі на захід від своєї відправної точки. Знайдіть загальну відстань, яку Мішель пройшла від своєї відправної точки.

Змішаний відгук

Вирішити $(x−4)^2=121$ .
Що таке $GCF$ $21ab^4$ і $15a^7b^2$ ?
Оцініть $_10C_7$ і поясніть його значення.
Фактор $6x^2+17x+5$ .
Знайдіть площу прямокутника довжиною $(16+2m)$ і шириною $(12+2m)$ .
Фактор $x^2−81$ .

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 11.7.

Лексика

Термін	Визначення
Формула відстані	Відстань між двома точками\) (x_1, y_1)\) та\) (x_2, y_2)\) можна визначити як\) d=\ sqrt {(x_2−x_1) ^2+ (y_2−y_1) ^2}\).
Формула середньої точки	Формула середньої точки говорить, що для кінцевих точок $(x_1,y_1)$ і $(x_2,y_2)$ , середина є $(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2})$ .

Додаткові ресурси

Інтерактивний елемент

Відео: Формула дистанції

Діяльність: Питання обговорення формули відстані

Практика: Формула відстані та алгебра

Реальний світ: Карта SF - PythM