4.37: Формула відстані та теорема Піфагора
- Page ID
- 54701
Відкрийте довжини сторін трикутника за допомогою теореми Піфагора. Визначте відстань як гіпотенузу прямокутного трикутника. Визначте відстань між впорядкованими парами.
Під час прогулянки до школи одного дня ви вирішите використовувати свої знання теореми Піфагора, щоб визначити, наскільки вона знаходиться між вашим будинком і школою. Ви знаєте, що ви ходите 3 квартали на схід, а потім поверніть і пройдіть 7 кварталів на північ, щоб дістатися до школи. Чи можна використовувати теорему Піфагора, щоб допомогти вам визначити «пряму» відстань між вашим будинком і школою?
Визначення відстані за допомогою теореми Піфагора
Ви можете використовувати теорему Піфагора, щоб знайти відстань між двома точками.
Розглянемо пункти\((-1, 6)\) і\((5, -3)\). Якщо ми розмістимо ці точки на сітці і з'єднаємо їх, вони роблять діагональну лінію. Намалюйте вертикальну лінію вниз\((-1, 6)\) і горизонтальну лінію зліва, щоб створити\((5, -3)\) прямокутний трикутник.
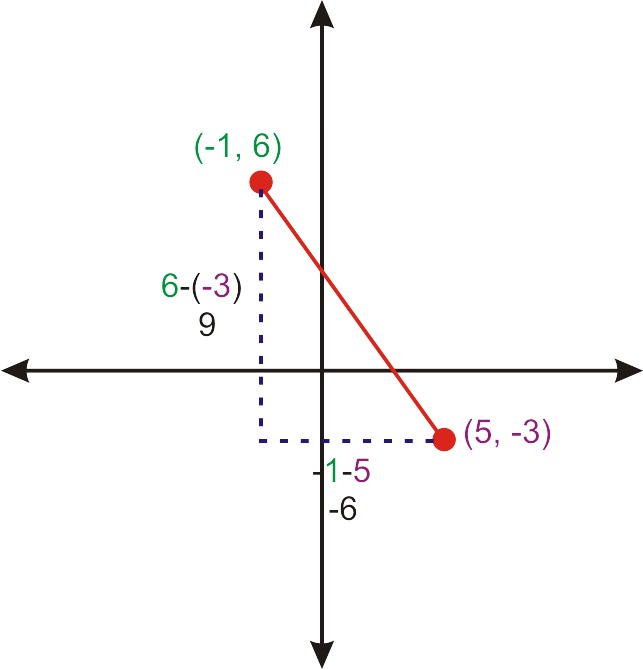
Тепер ми можемо знайти відстань між цими двома точками, використовуючи вертикальні та горизонтальні відстані, які ми визначили на графіку.
\(\begin{align*} 9^2+(−6)^2&=d^2 \\ 81+36&=d^2 \\ 117&=d^2 \\ \sqrt{117}&=d \\ 3\sqrt{13}&=d\end{align*}\)
Зверніть увагу, що значення x віднімали один від одного, щоб знайти відстань по горизонталі, а значення y віднімали один від одного, щоб знайти відстань по вертикалі. Якщо цей процес узагальнено для двох точок\ ((x_1, y_1) та\ ((x_2, y_2), виводиться формула відстані.
\((x_1−x_2)^2+(y_1−y_2)^2=d^2\)
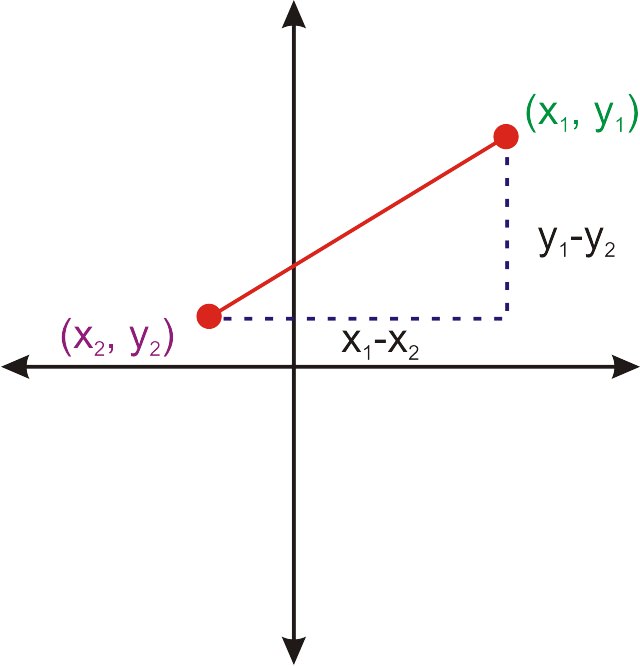
Це теорема Піфагора з вертикальними і горизонтальними відмінностями між\((x_1, y_1)\) і\((x_2, y_2)\). Взявши квадратний корінь з обох сторін вирішить праву сторону для d, відстань.
\(\sqrt{(x_1−x_2)^2+(y_1−y_2)^2}=d\)
Це формула відстані. Наступні проблеми показують, як застосувати формулу відстані.
Застосування формули відстані
1. Знайдіть відстань між двома точками.
\((4, 2)\)і\((-9, 5)\)
Підключіть кожну пару точок до формули відстані.
\(\begin{align*}d & =\sqrt{(4−(−9))^2+(2−5)^2} \\ &=\sqrt{13^2+(−3)^2} \\ &=\sqrt{169+9} \\ &=\sqrt{178}\end{align*}\)
2. Знайдіть відстань між двома точками.
\((-10, 3)\)і\((0, -15)\)
Підключіть кожну пару точок до формули відстані.
\(\begin{align*}d & =\sqrt{(−10−0)^2+(3−(−15))^2} \\ &=\sqrt{(−10)^2+(18)^2} \\ &=\sqrt{100+324} \\ &=\sqrt{424}=2\sqrt{106}\end{align*}\)
3. Знайдіть відстань між двома точками.
\((3, 1)\)і\((2, -7)\)
Підключіть кожну пару точок до формули відстані.
\(\begin{align*}d&=\sqrt{(3−2)^2+(1−(−7))^2} \\ &=\sqrt{(1)^2+(8)^2} \\ &=\sqrt{1+64} \\ &=\sqrt{65}\end{align*}\)
Приклад\(\PageIndex{1}\)
Раніше вас попросили використовувати свої знання теореми Піфагора, щоб визначити, наскільки вона знаходиться між вашим будинком і школою.
Рішення
Оскільки ви знаєте, що поїздка до школи передбачає ходьбу 3 кварталами на схід, а потім 7 блоків на північ, ви можете побудувати трикутник на системі координат з цих довжин, як це:
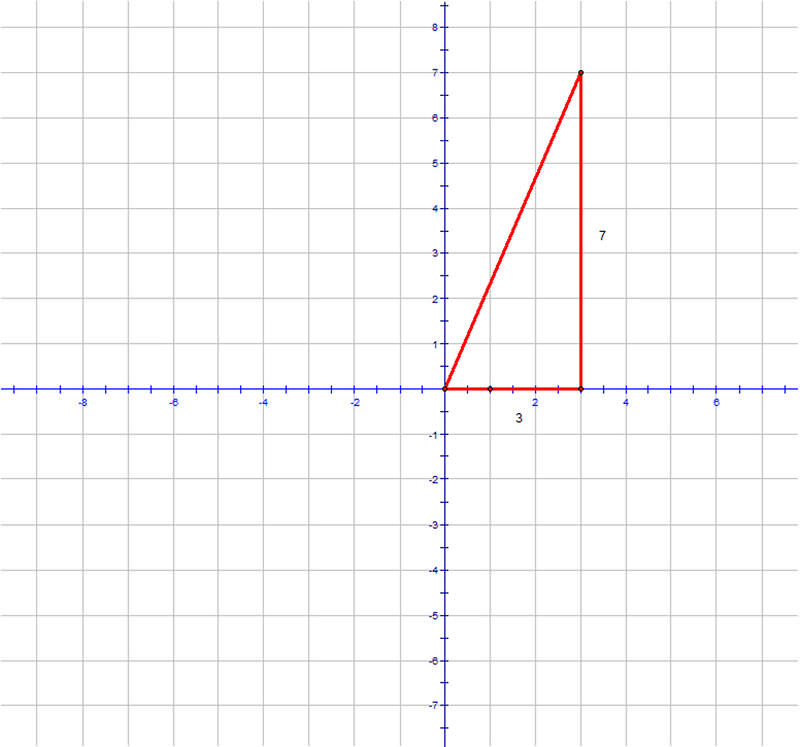
Оскільки ви пішли трьома кварталами на схід, школа має "\(x\)" координату 3. Так само, оскільки ви пішли 7 кварталів на північ, школа має\(y\) "" координату 7. Щоб знайти пряму відстань до школи, можна скористатися формулою відстані:
\(\begin{align*}d&=\sqrt{(3−0)^2+(7−0)^2} \\ &=\sqrt{(3)^2+(7)^2} \\ &=\sqrt{58}\end{align*}\)
Це пряма відстань приблизно 7,6 блоків.
Приклад\(\PageIndex{2}\)
Знайдіть відстань між двома точками.
\ (3, 1) і\ (2, -7)
Рішення
Підключіть кожну пару точок до формули відстані.
\(\begin{align*}d&=\sqrt{(3−2)^2+(1−(−7))^2 \\ &=\sqrt{(1)^2+(8)^2} \\ &=\sqrt{1+64} \\ &=\sqrt{65}\end{align*}\)
Приклад\(\PageIndex{3}\)
Знайдіть відстань між двома точками.
\ (5, -8) і\ (0, 3)
Рішення
Підключіть кожну пару точок до формули відстані.
\(\begin{align*}d&=\sqrt{(5−0)^2+(−8−(3))^2} \\ &=\sqrt{(5)^2+(−11)^2} \\ &=\sqrt{25+121} \\ =\sqrt{146}\end{align*}\)
Приклад\(\PageIndex{4}\)
Знайдіть відстань між двома точками.
\((2, 6) \)і\((2, 9)\)
Рішення
Підключіть кожну пару точок до формули відстані.
\(\begin{align*}d &=\sqrt{(2−2)^2+(6−9)^2} \\ &=\sqrt{(0)^2+(−3)^2 \\ &=\sqrt{9} \\ =3\end{align*}\)
Рецензія
Знайдіть відстань між кожною парою точок. Округляйте кожну відповідь до найближчої десятої.
- \((2, 4)\)і\((5, 10)\)
- \((1, 5)\)і\((8, 9)\)
- \((-2, 3)\)і\((6, 4)\)
- \((5, 7)\)і\((5, 10)\)
- \((8, 12)\)і\((15, 12)\)
- \((1, -4)\)і\((25, -2)\)
- \((5, -6)\)і\((3, 7)\)
- \((12, -9)\)і\((-1, 5)\)
- \((-3, 14)\)і\((8, 10)\)
- \((-11, 3)\)і\((-5, 1)\)
- \((5, 2)\)і\((11, 13)\)
- \((8, 10)\)і\((9, -6)\)
Знайдіть периметр кожного трикутника. Округляйте кожну відповідь до найближчої десятої.
- \(A(3,−5),\:B(−5,−8),\:C(−2,7)\)
- \(A(5,3),\:B(2,−7),\:C(−1,5)\)
- \(A(1,2),\:B(1,5),\:C(4,5)\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.4.
Лексика
| Термін | Визначення |
|---|---|
| Формула відстані | Відстань між двома точками\((x_1,y_1)\) і\((x_2,y_2)\) може бути визначено як\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\). |
Додаткові ресурси
Інтерактивний елемент
Відео: Формула відстані
Практика: Формула відстані та теорема Піфагора
Реальний світ: Все залежить від відстані