4.38: Відстань між паралельними лініями

Last updated
Save as PDF

Page ID: 54812

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Довжина перпендикулярного відрізка між паралельними лініями.

Всі вертикальні лінії мають форму\(x=a\), де\(a\) знаходиться\(x\) -перехоплення. Щоб знайти відстань між двома вертикальними лініями, порахуйте квадрати між двома лініями. Ви можете використовувати цей метод і для горизонтальних ліній. Всі горизонтальні лінії мають форму\(y=b\), де\(b\) знаходиться\(y\) -перехоплення.

Взагалі, найкоротша відстань між двома паралельними лініями - це довжина перпендикулярного відрізка між ними. Перпендикулярних відрізків між двома паралельними лініями нескінченно багато, але всі вони будуть однакової довжини.

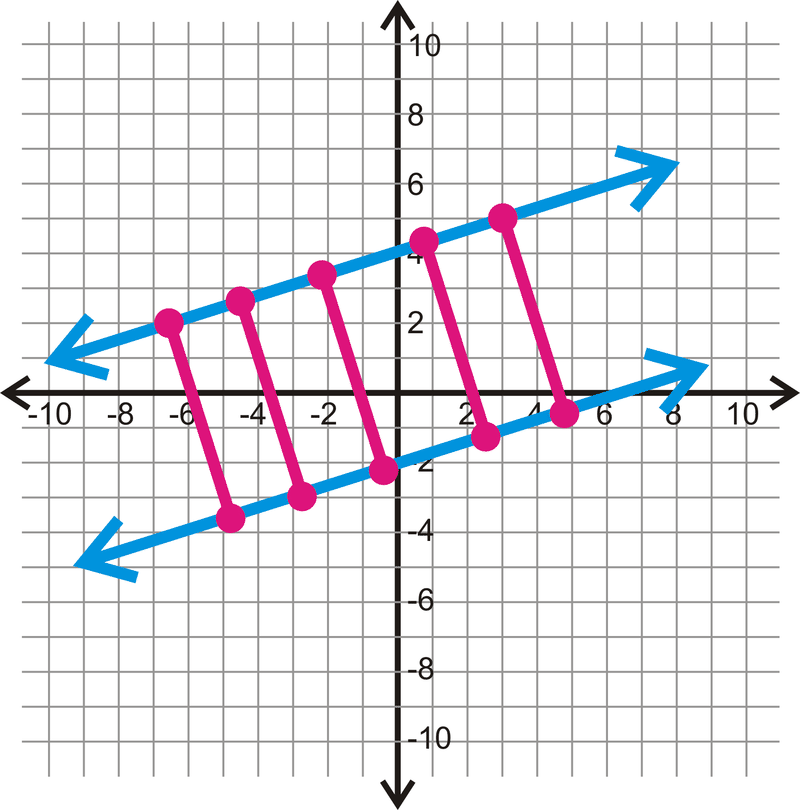
Ф-д_А 5654А10Ф6ЕФ82Ф03Б3А166Е4С290Д7ФА1582402ЕА756ФК0200к16Ф+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Пам'ятайте, що відстані завжди позитивні!

Приклад\(\PageIndex{1}\)

Знайти відстань між\(x=3\) і\(x=-5\).

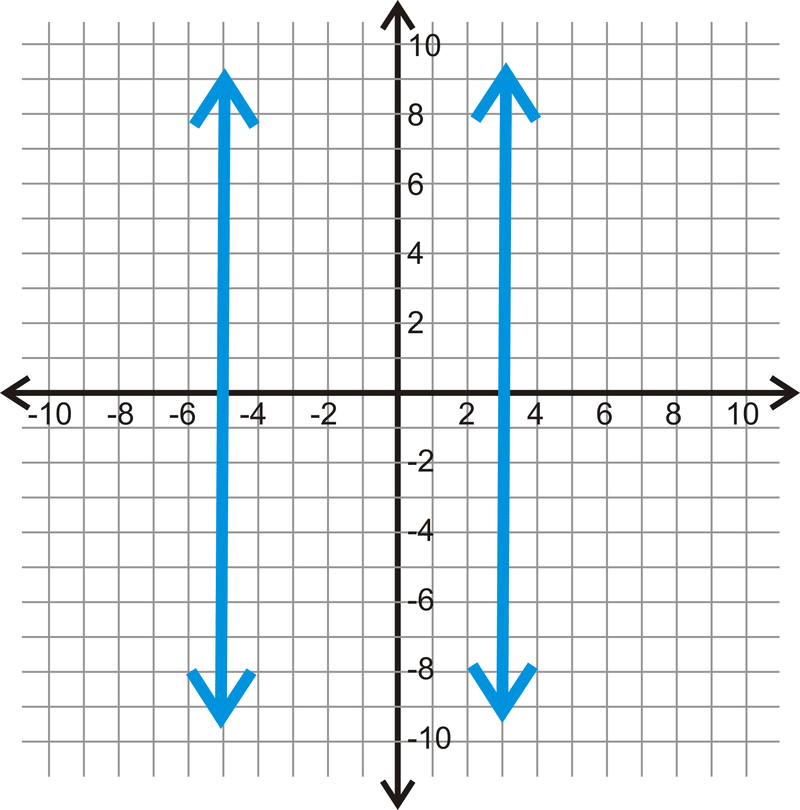
F-д_73А5 ЕД ФБ5А83Е601А9684А35С3Е4Д9135Д085876А977ЕБ14БФ1Б0ЕА+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Рішення

Дві лінії\(3 – (-5)\) одиниць один від одного, або 8 одиниць один від одного.

Приклад\(\PageIndex{2}\)

Знайти відстань між\(x=-5\) і\(x=-10\).

Рішення

Дві лінії\(-5 – (-10)\) одиниць один від одного, або 5 одиниць один від одного.

Приклад\(\PageIndex{3}\)

Знайти відстань між\(y=5\) і\(y=-8\).

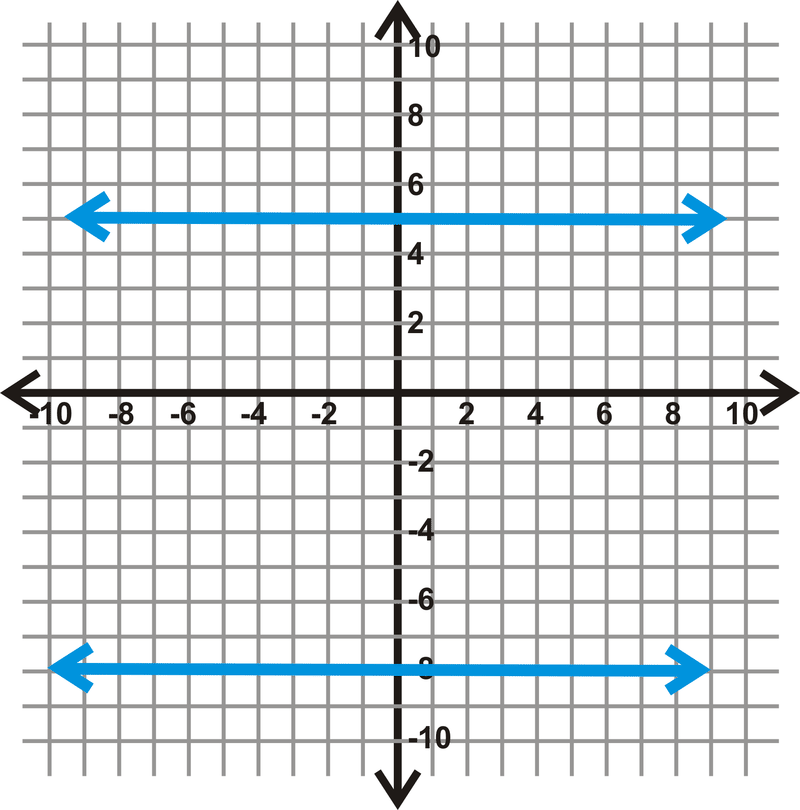
F-D_01841C05D72 ЕФ3С9С43Е45А95КС0 ЕЕ4391Д30Б9916842Б204+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Рішення

Дві лінії\(5 – (-8)\) одиниць один від одного, або 13 одиниць один від одного.

Приклад\(\PageIndex{4}\)

Знайти відстань між\(y=x+6\) і\(y=x−2\).

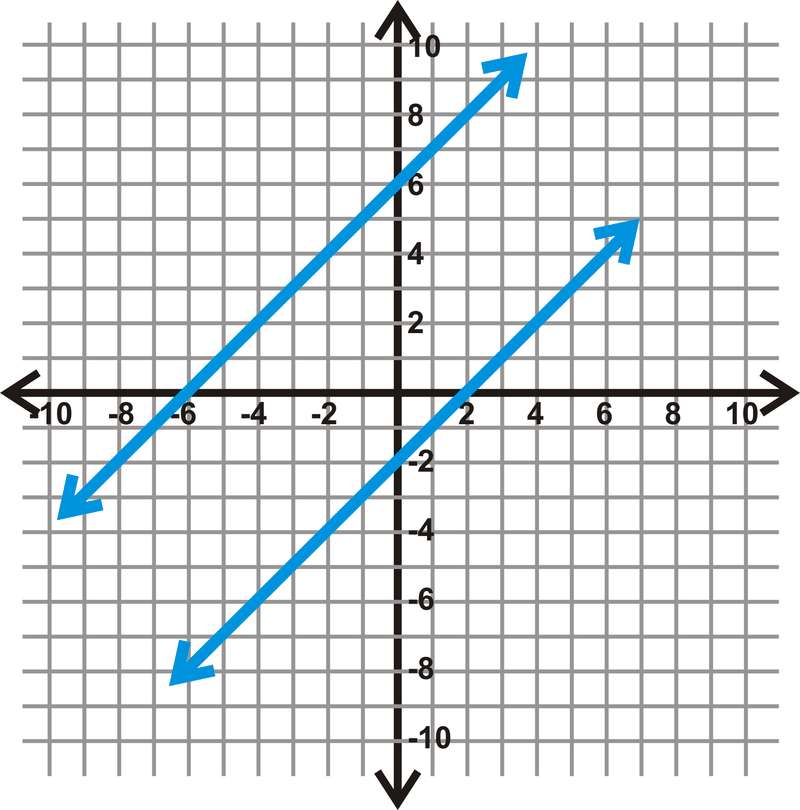
F-Д_ДДА 43СЕ 8031БД9Д34ЕЦ5С4 Фе 9А68Б6Б40С180 CF987ФДФ 4A0477A0D3A+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Рішення

Крок 1: Знайдіть перпендикулярний нахил.

\(m=1\), Отже\(m_{\perp} =-1\).

Крок 2: Знайдіть y-перехоплення верхньої лінії,\(y=x+6\).

Перехоплення є\((0, 6)\).

Крок 3: Використовуйте нахил і відлік вниз 1 і вправо 1, поки не вдарите\(y=x−2\).

Завжди піднімається/запускайте однакову суму для\(m=1\) або\(m=-1\).

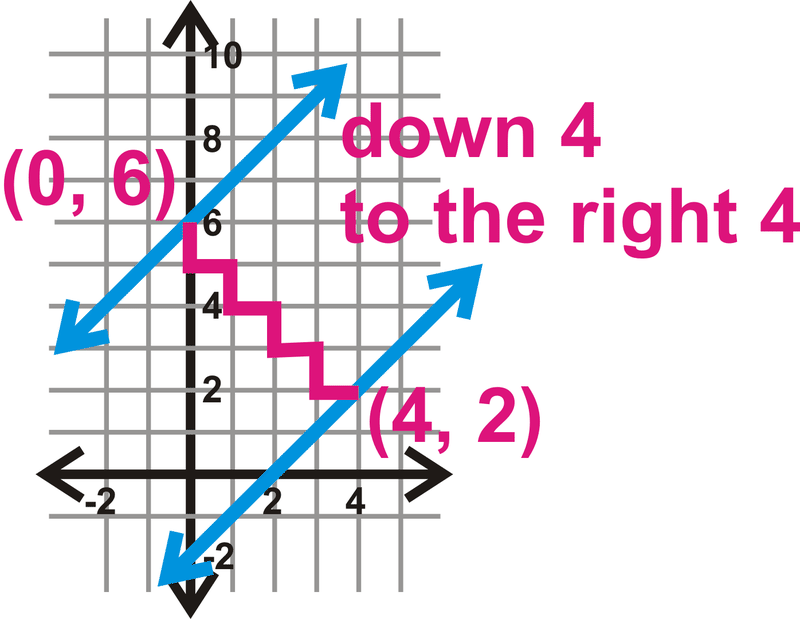
F-D_66AC 1Ф309 ПК-ДБ9ББ4А8Д56722 постійного струму DD0F5D4EA2C94F5A4051D7775+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Крок 4: Використовуйте ці дві точки у формулі відстані, щоб визначити, наскільки далеко розташовані лінії.

\(\begin{align*} d&=\sqrt{(0−4)^2+(6−2)^2} \\ &=\sqrt{(−4)^2+(4)^2} \\ &=\sqrt{16+16} \\ &=\sqrt{32}=5.66\: units\end{align*}\)

Приклад\(\PageIndex{5}\)

Знайти відстань між\(y=-x−1\), і\(y=-x−3\).

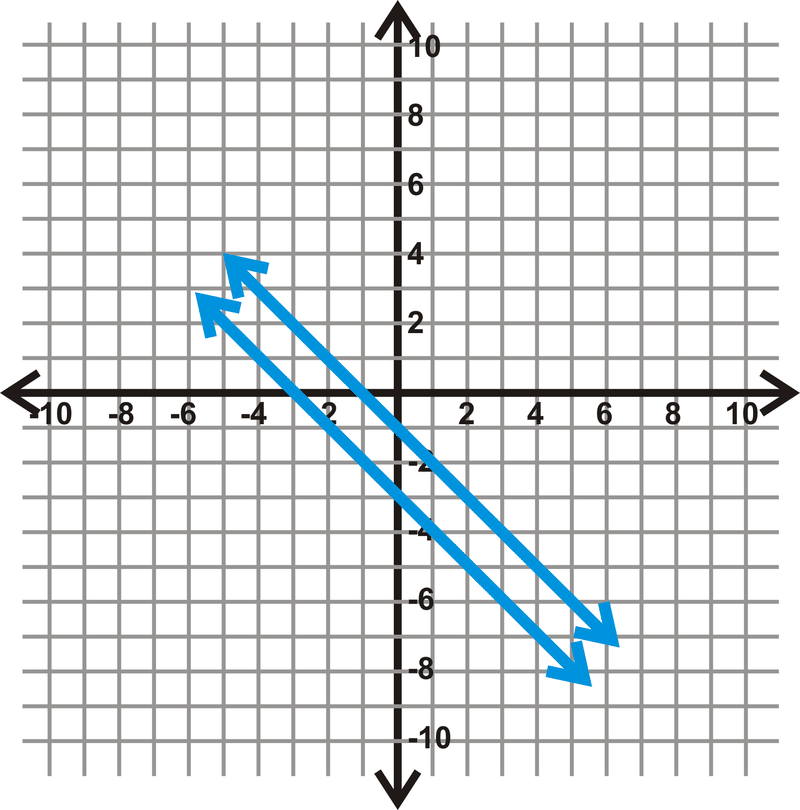
F-д_17а69 кб 952 С6Д5Е771А1БФ 8579ФБ3 ACD295E0436375DA06B960FDCCE+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Рішення

Крок 1: Знайдіть перпендикулярний нахил.

\(m=-1\), Отже\(m_{\perp} =1\).

Крок 2: Знайдіть y-перехоплення верхньої лінії,\(y=-x−1\).

Перехоплення є\((0, -1)\).

Крок 3: Використовуйте нахил і відлік вниз 1 і вліво 1, поки не вдарите\(y=x−3\).

F-д_Е7 КБА 0Е239341827 ЕС5 ДФФ 12А53279Е6985239990663 БК2E3E41E002+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{7}\)

Крок 4: Використовуйте ці дві точки у формулі відстані, щоб визначити, наскільки далеко розташовані лінії.

\(\begin{align*} d&=\sqrt{(0−(-1))^2+(-1−(-2))^2} \\ &=\sqrt{(1)^2+(1)^2} \\ &=\sqrt{1+1} \\ &=\sqrt{2}=1.41\: units \end{align*}\)

Рецензія

Використовуйте кожен графік нижче, щоб визначити, наскільки далеко один від одного кожна пара паралельних ліній.

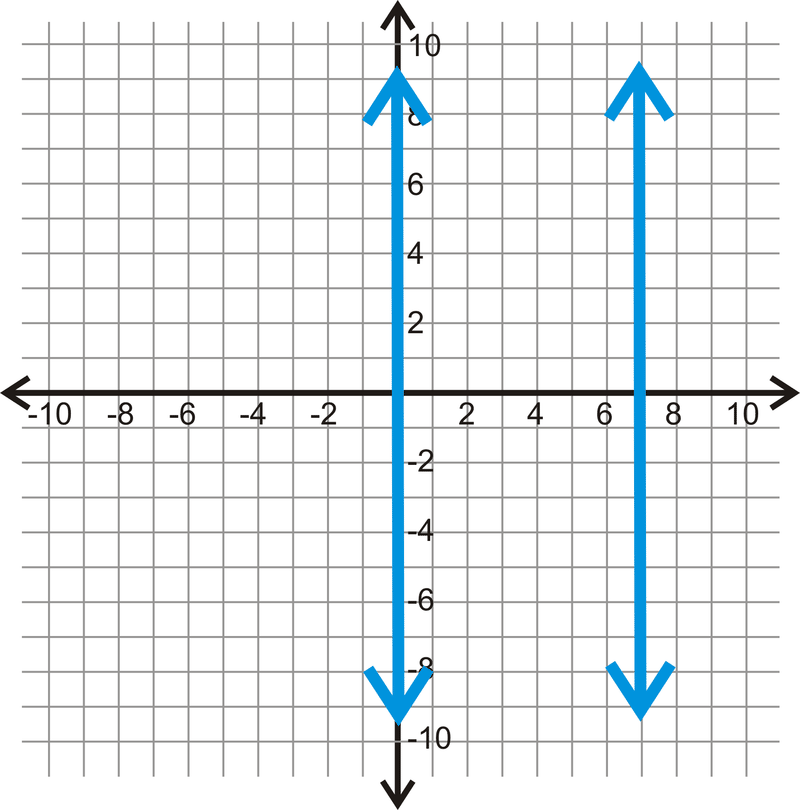
Малюнок\(\PageIndex{8}\)
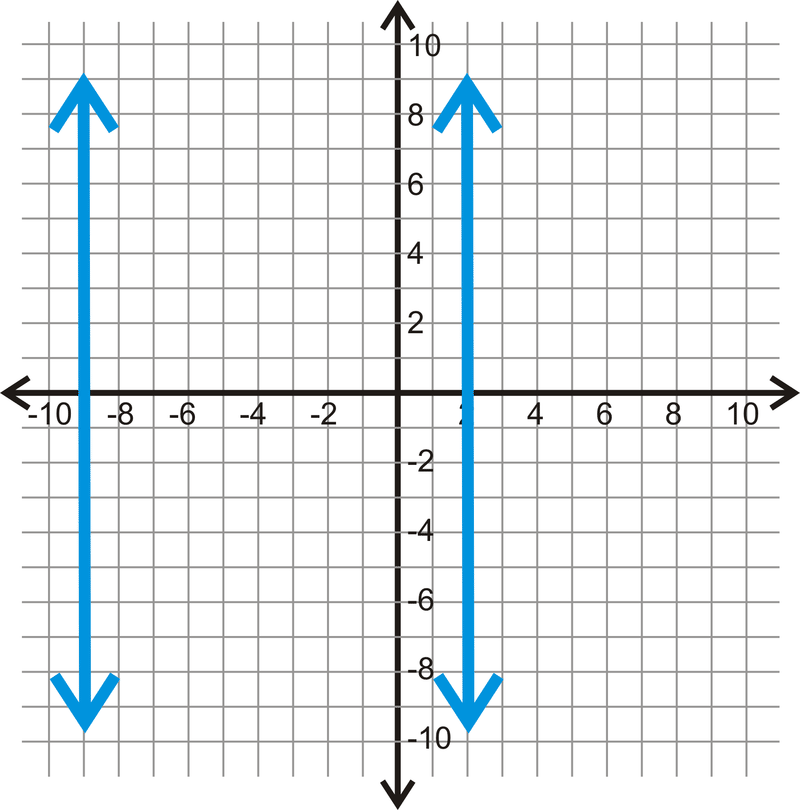
Малюнок\(\PageIndex{9}\)
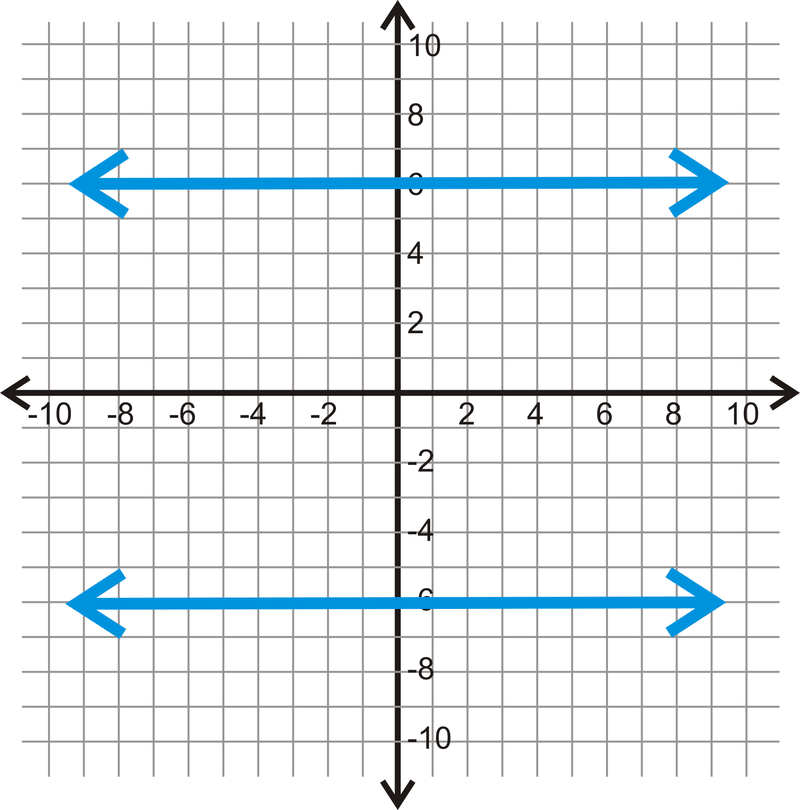
Малюнок\(\PageIndex{10}\)
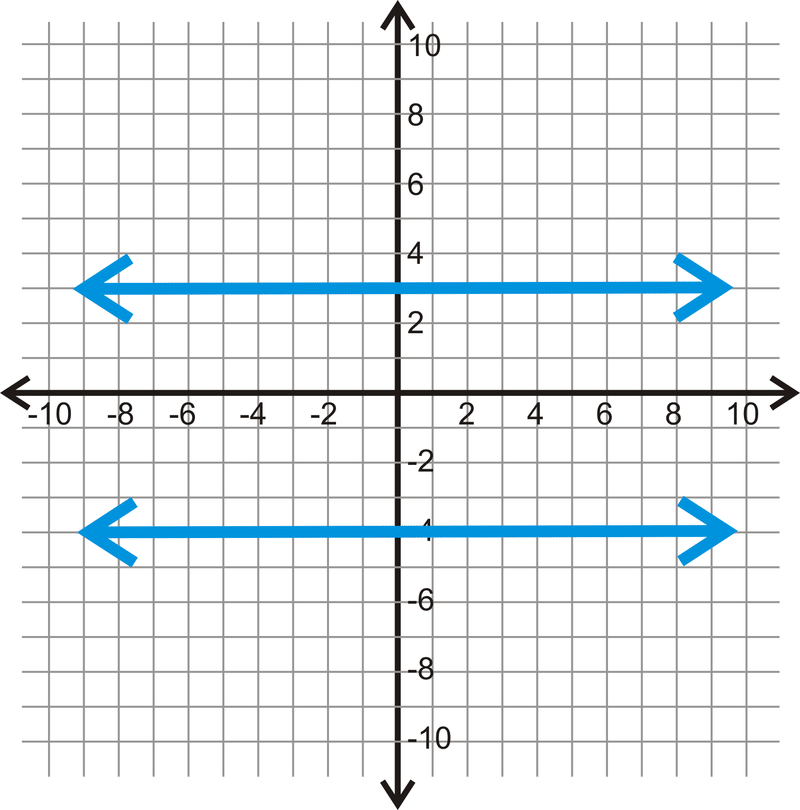
Малюнок\(\PageIndex{11}\)

Визначте найкоротшу відстань між кожною парою паралельних ліній. Округлите відповідь до найближчої сотої.

\(x=5\),\(x=1\)
\(y=−6\),\(y=4\)
\(y=3\),\(y=15\)
\(x=−10\),\(x=−1\)
\(x=8\),\(x=0\)
\(y=7\),\(y=−12\)

Знайти відстань між заданими паралельними лініями.

\(y=x−3\),\(y=x+11\)
\(y=−x+4\),\(y=−x\)
\(y=−x−5\),\(y=−x+1\)
\(y=x+12\),\(y=x−6\)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 3.11.

Ресурси

Лексика

Термін	Визначення
Формула відстані	Відстань між двома точками\((x_1,y_1)\) і\((x_2,y_2)\) може бути визначено як\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\).
Перпендикуляр	Перпендикулярні лінії - це лінії, які перетинаються під\(90^{\circ}\) кутом. Твір ухилів двох перпендикулярних ліній дорівнює -1.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи пошуку відстані між паралельними лініями - основні

Діяльність: Відстань між паралельними лініями Питання обговорення

Навчальні посібники: лінії в координатній площині

Практика: Відстань між паралельними лініями

Реальний світ: Вигортання