4.1: Класифікувати трикутники

Last updated
Save as PDF

Page ID: 54714

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Класифікувати трикутники як гострі, праві, тупі або рівнокутні і як шкала, рівнобедрений або рівносторонній. Використовуйте класифікації, щоб знайти відсутню інформацію.

Класифікація трикутників

Трикутник - це будь-яка замкнута фігура, виконана трьома відрізками лінії, що перетинаються в їх кінцевих точках. Кожен трикутник має три вершини (точки, де зустрічаються сегменти), три сторони (відрізки) та три внутрішні кути (утворені на кожній вершині). Всі наступні форми - це трикутники.

F-д_д8c6379c0e8f8869385631c4846a2d049 тадддб530c1ad7344df8de3+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Сума внутрішніх кутів у трикутнику дорівнює\(180^{\circ}\). Це називається теоремою про суму трикутника і обговорюється далі в концепції «Теорема про суму трикутника».

Кути можна класифікувати за своїми розмірами як гострі, тупі або правильні. У будь-якому трикутнику два кути завжди будуть гострими. Третій кут може бути гострим, тупим або правим. Класифікуємо кожен трикутник за цим кутом.

Прямокутний трикутник: Трикутник з одним прямим кутом.

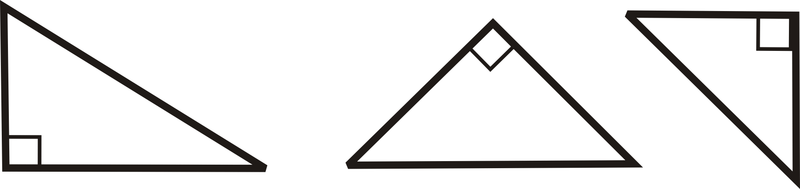
F-D_8 ЕД 52Е1А2 Е7ЕБ5458712Д830ФБ Б 37БФ 014С53ЕА4 ЦБД 7CF844B3BD+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Тупий трикутник: трикутник з одним тупим кутом.

F-д_БФК 9480А30Б71 А6509С5А7191А0А71838Д82131С46Е769Е88Б192+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Гострий трикутник: трикутник, де всі три кути є гострими.

F-D_14754 ЕЕЕД 5 ФБ 5АА517Ф5 АБФ 2Е2340Б050Е0044Б1Б77А9631Е02+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Рівнокутний трикутник: трикутник, де всі кути конгруентні.

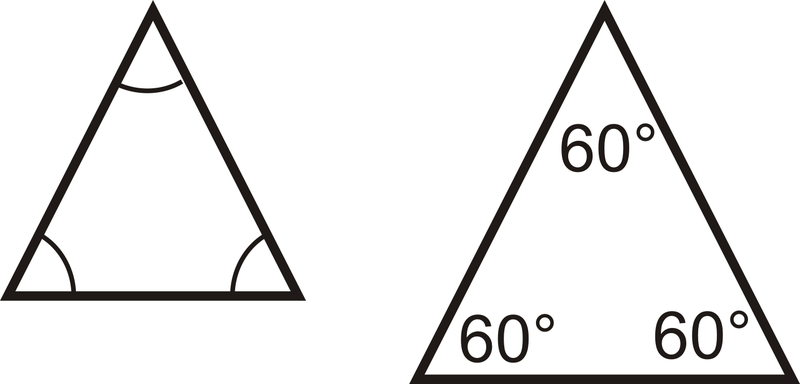
Ф-д_ліжко 2де 60Б04531 ББФ 632САДС682990 ФА58212Е 89А805017ДФ6ДБ275+зображення_крихіткий+зображення_крихітка_крихітка_png — Малюнок\(\PageIndex{5}\)

Також можна класифікувати трикутник по його сторонам.

Scalene трикутник: трикутник, де всі три сторони мають різну довжину.

F-D_D3B6E310DC 467173153 АФ 26 ББД 29 ББД 5691 АБ7Ф9 ЕЕЦ5982Ф3C62004+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Рівнобедрений трикутник: трикутник з принаймні двома конгруентними сторонами.

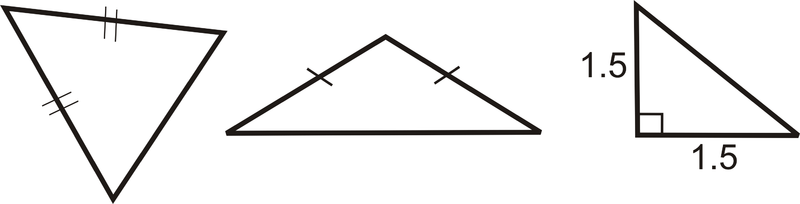
F-D_8061 А0 ДБ95831615Б94ДК 372Е69С354А0Д480Ф20697 ABFE 640616F5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{7}\)

Рівносторонній трикутник: трикутник з трьома конгруентними сторонами.

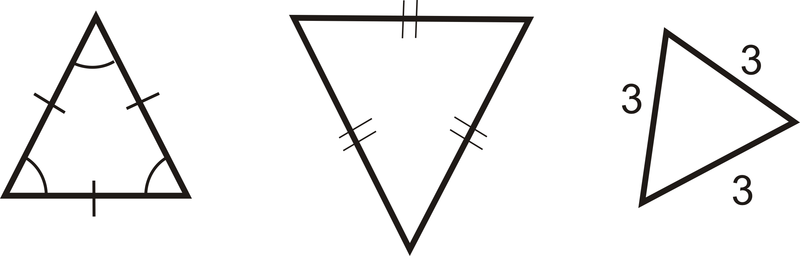
F-D_02249522B7113A5D03711 БЕ43379 ФЕА 3СЕ9БФ011 БД26ДА011ЕФ664D+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{8}\)

Відзначимо, що з визначень рівносторонній трикутник - це також рівнобедрений трикутник.

Що робити, якщо вам дали кутові заходи та/або довжини сторін трикутника? Як би ви описали трикутник на основі цієї інформації?

Приклад\(\PageIndex{1}\)

Які з наведених нижче фігур не є трикутниками?

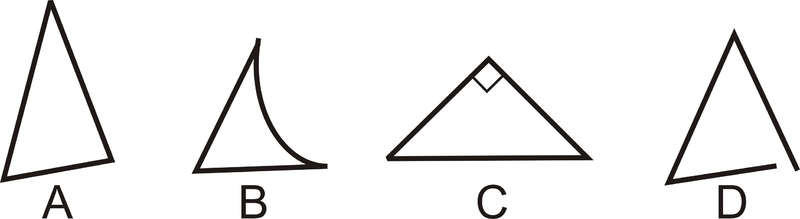F-д_FF51 ДБФ 573731 ФЦ7 АФ 363 ЕД5Е2Б8Е927АФДФ 4699803713427E9+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{9}\)

Рішення

B - це не трикутник, оскільки він має одну вигнуту сторону. D не замкнутий, тому це теж не трикутник.

Приклад\(\PageIndex{2}\)

Скільки трикутників на схемі нижче?

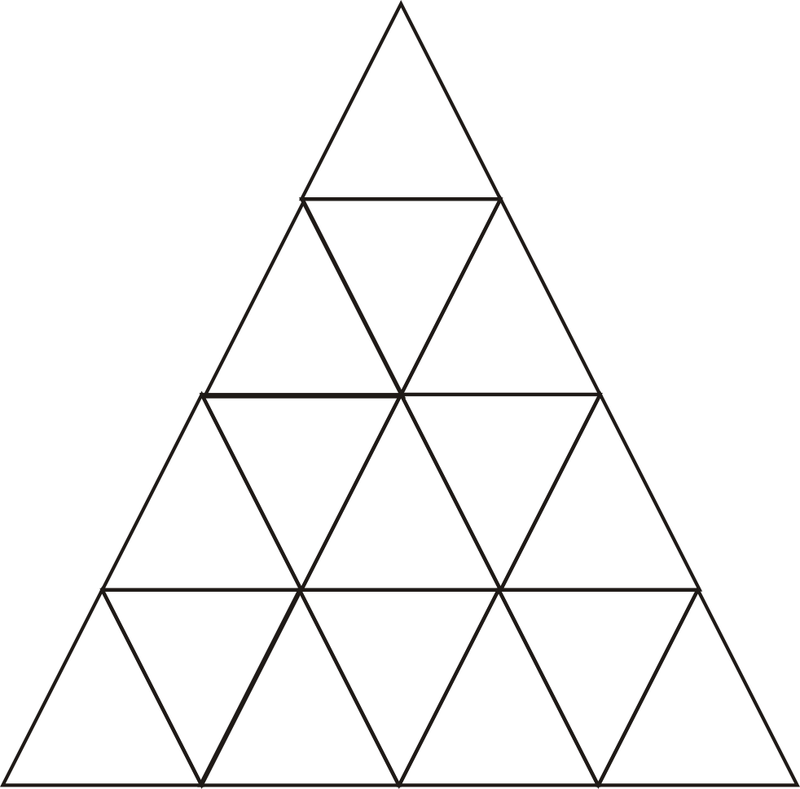F-D_80720053E15144ФФ+ФФ 165ФФ Ф 0307Ф80311А395164Ф7011Ф+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{10}\)

Рішення

Почніть з підрахунку найменших трикутників, 16.

Тепер порахуйте трикутники, які утворені 4 меншими трикутниками, 7.

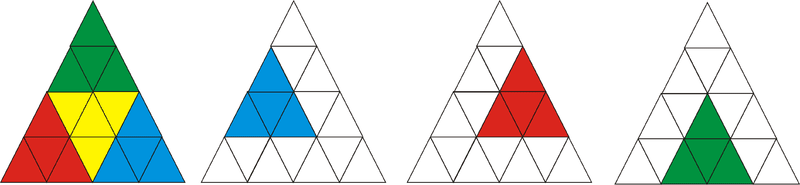F-д_95БФБ2221533Д9Б22079 АФ1Д0Е8Б1Ф27Д53Е5719Е69КФА54С6Ф77ААФ+зображення_крихіткий+зображення_крихіткий.PNG

Далі порахуйте трикутники, які утворені 9 дрібних трикутників, 3.

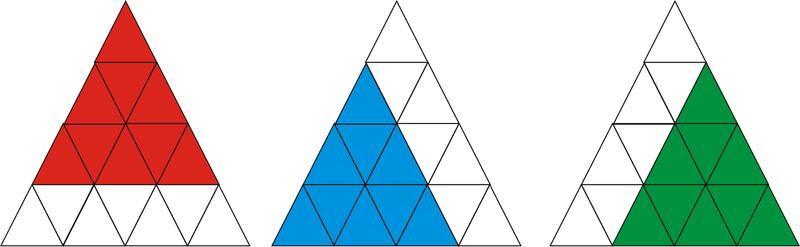
Ф-Д_БФ 1182Е36Д2А1С82Б1С37568А673Б04ББ Деф 9А4Ф9А57КД 686D16C6+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{12}\)

Нарешті, є один трикутник, утворений усіма 16 меншими трикутниками. Склавши ці цифри воєдино, отримуємо\(16+7+3+1=27\).

Приклад\(\PageIndex{3}\)

True або false: Рівносторонній трикутник рівнокутний.

Рішення

Правда. Рівносторонні трикутники мають внутрішні кути, які всі конгруентні, тому вони рівнокутні.

Приклад\(\PageIndex{4}\)

Який термін найкраще описує\(\Delta RST\) нижче?

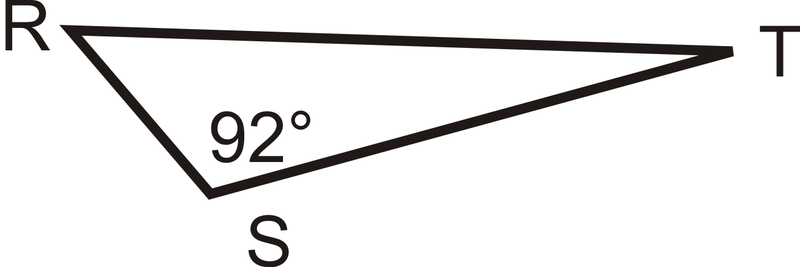
Ф-Д_12ФД1С76Е6БДС3426 ФДБ28АД 15Е4Ф53Е8316491056ДА7Ф65А68Д7С9+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{13}\)

Рішення

Цей трикутник має один позначений тупим кутом\(92^{\circ}\). Трикутники можуть мати тільки один тупий кут, тому це тупий трикутник.

Приклад\(\PageIndex{5}\)

Класифікувати трикутник за його сторонами і кутами.

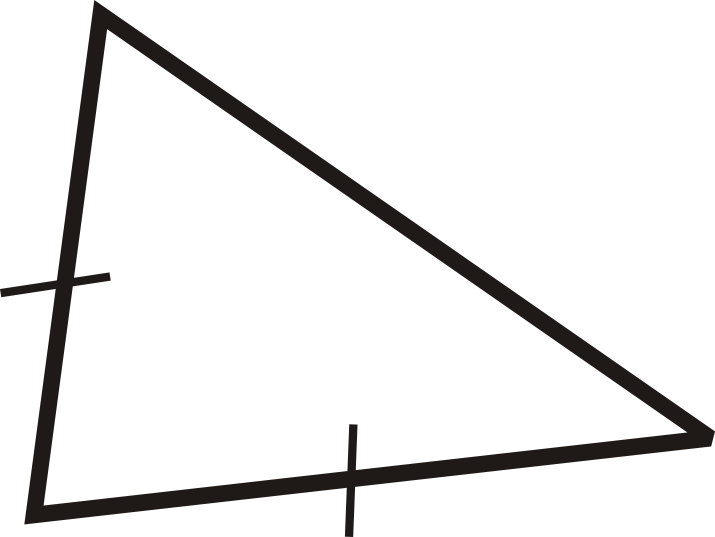
F-D_A38EBF9 ЕЕЕФ 5Е8 ДДБ 0ДД2С0674760С870А09Д222СБ31А7Д63АЕБ1С3+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{14}\)

Рішення

Ми бачимо, що є дві конгруентні сторони, тому вона рівнобедрена. За кутами всі вони виглядають гостро. Ми говоримо, що це гострий рівнобедрений трикутник.

Рецензія

Для питань 1-6 класифікуйте кожен трикутник за його сторонами та кутами.

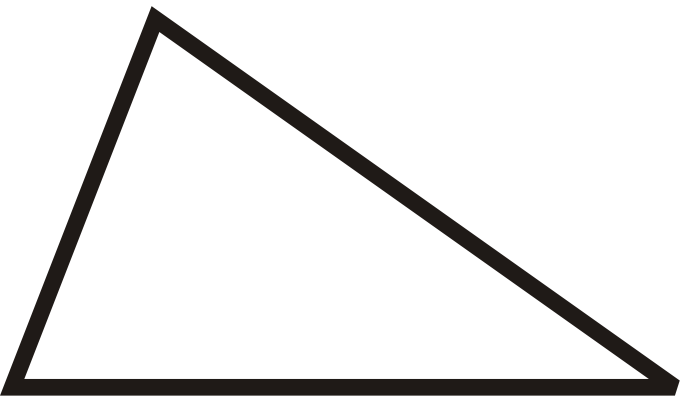
Малюнок\(\PageIndex{15}\)
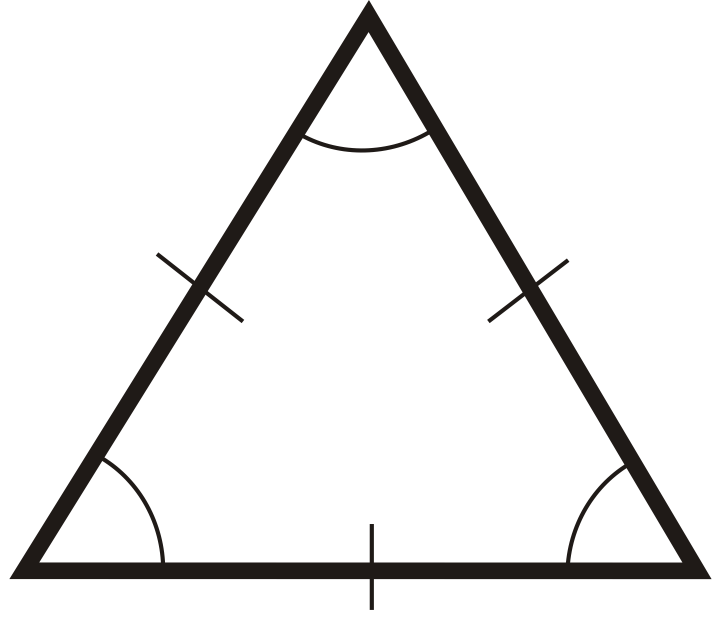
Малюнок\(\PageIndex{16}\)
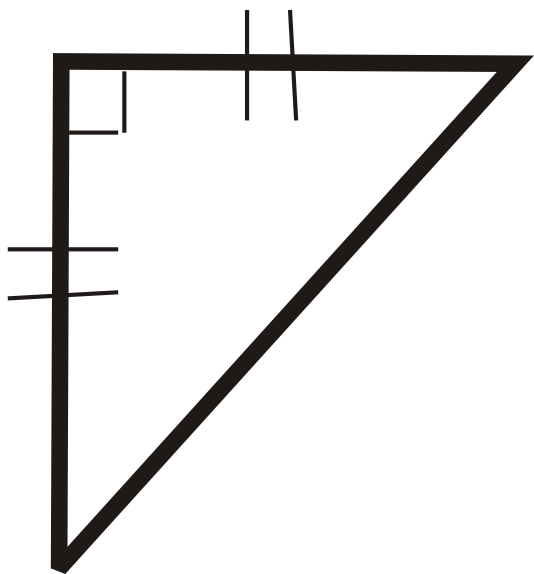
Малюнок\(\PageIndex{17}\)
Малюнок\(\PageIndex{18}\)
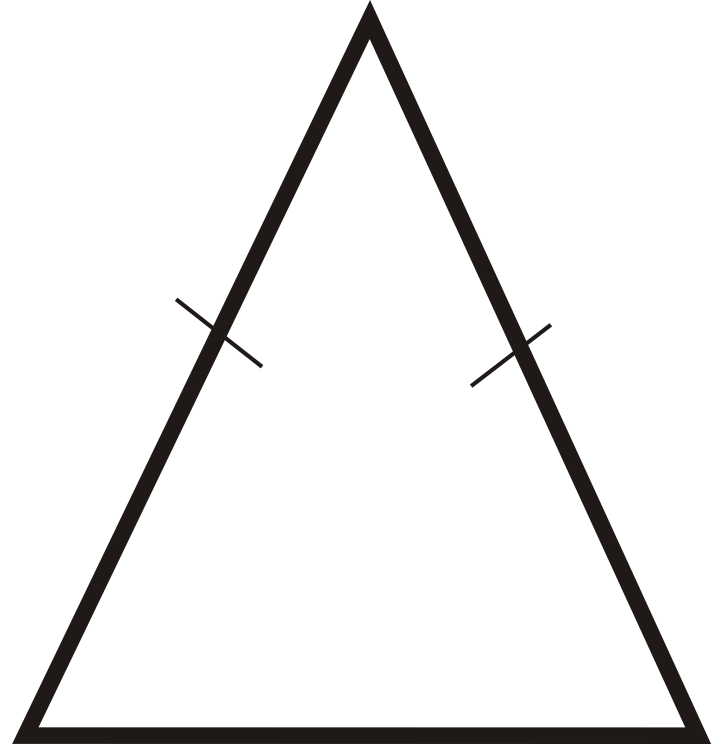
Малюнок\(\PageIndex{19}\)
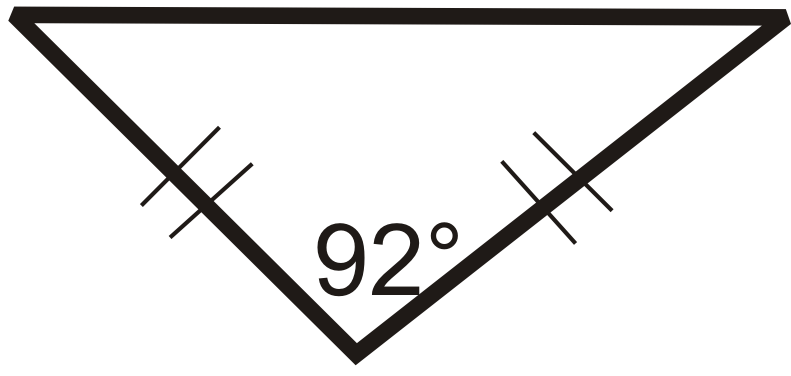
Малюнок\(\PageIndex{20}\)
Чи можете ви намалювати трикутник з прямим кутом і тупим кутом? Чому чи чому ні?
У рівнобедреному трикутнику можуть кути, протилежні конгруентним сторонам, тупими?

Для 9-10 визначте, чи є твердження істинним чи хибним.

Тупі трикутники можуть бути рівнобедреними.
Прямокутний трикутник гострий.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.11.

Ресурси

Лексика

Термін	Визначення
Гострий трикутник	Гострий трикутник має три кути, кожен з яких вимірює менше 90 градусів.
рівнокутний трикутник	Трикутник з усіма конгруентними кутами.
рівносторонній трикутник	Трикутник з трьома конгруентними сторонами.
Рівнобедрений трикутник	Рівнобедрений трикутник - це трикутник, у якого рівно дві сторони мають однакову довжину.
Тупий трикутник	Тупий трикутник - це трикутник з одним кутом, який більше 90 градусів.
Сценовий трикутник	Скальний трикутник - це трикутник, в якому всі три сторони мають різну довжину.
Трикутник	Трикутник - це багатокутник з трьома сторонами і трьома кутами.
Внутрішні кути	Внутрішні кути - це кути всередині фігури.
Прямокутний	Прямим кутом називається кут, рівний 90 градусам.
Рівносторонній	Багатокутник рівносторонній, якщо всі його сторони мають однакову довжину.
Рівнокутні	Багатокутник є рівнокутним, якщо всі кути однакові.

Додаткові ресурси

Інтерактивний елемент

Відео: Кутові відносини і типи трикутників

Види діяльності: Класифікація трикутників Питання обговорення

Навчальні посібники: Полігони Навчальний посібник

Практика: Класифікувати трикутники

Реальний світ: Мости над неспокійною водою