Skip to main content
LibreTexts - Ukrayinska

4.26: Теорема нерівності трикутника

  1. Last updated
  2. Save as PDF
  • Page ID
    54702

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Чи можуть будь-які три довжини зробити трикутник? Відповідь - ні. Наприклад, довжини 1, 2, 3 не можуть зробити трикутник\(1+2=3\), тому що вони всі лежать на одній лінії. Довжини 4, 5, 10 також не можуть зробити трикутник, тому що\(4+5=9<10\). Подивіться на фотографії нижче:

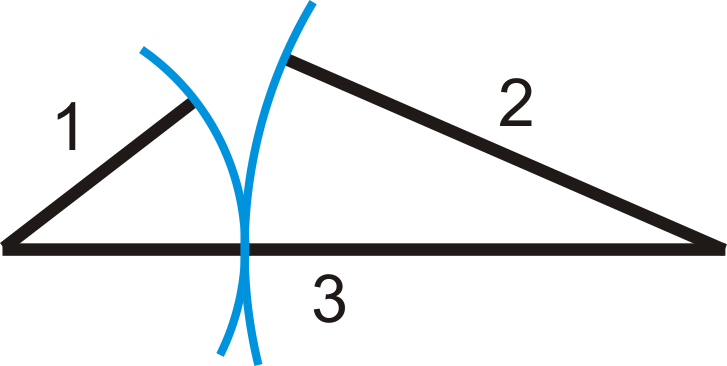
    F-D_46ЕФА 779Ф239 CDDC8С7Ф53Б45938Ф064ЕБ62ДБ7Б7Б4AD165+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Дуги показують, що дві сторони ніколи не зустрінуться, утворюючи трикутник.

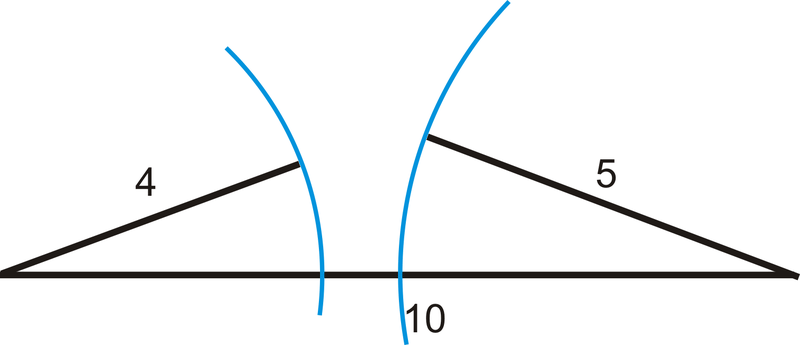
    F-D_EB5692D безкоштовно EEEC0d92E21A32b4FCE819855d481889 А30545522EA1C29+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Щоб вийшов трикутник, дві сторони повинні скласти, щоб бути більше третьої сторони. Це називається теоремою нерівності трикутника. Це означає, що якщо ви знаєте дві сторони трикутника, є лише певні довжини, якими може бути третя сторона. Якщо дві сторони мають довжину\(a\) і\(b\), то довжина третьої сторони, s, має діапазон\( a−b<s<a+b\).

    Що робити, якщо вам дали три довжини, як 5, 7 і 10? Як ви могли визначити, чи сторони з цими довжинами утворюють трикутник?

    Приклад\(\PageIndex{1}\)

    Чи роблять довжини 4.1, 3.5, 7.5 трикутник?

    Рішення

    Використовуйте теорему нерівності трикутника. Перевірте, щоб переконатися, що менші два числа складаються більше, ніж найбільше число.

    \(4.1+3.5>7.5\)і\(7.6>7.5\) так у ес ці довжини зробити трикутник.

    Приклад\(\PageIndex{2}\)

    Чи роблять довжини 4, 4, 8 трикутник?

    Рішення

    Використовуйте теорему нерівності трикутника. Перевірте, щоб переконатися, що менші два числа складаються більше, ніж найбільше число.

    \(4+8=12\)і\(12>11\) так так ці довжини зробити трикутник.

    Приклад\(\PageIndex{3}\)

    Чи роблять довжини 4, 11, 8 трикутник?

    Рішення

    Використовуйте теорему нерівності трикутника. Перевірте, щоб переконатися, що менші два числа складаються більше, ніж найбільше число.

    \(4+8=12\)і\(12>11\) так так ці довжини зробити трикутник.

    Приклад\(\PageIndex{4}\)

    Знайдіть довжину третьої сторони трикутника, якщо дві інші сторони 10 і 6.

    Рішення

    Теорема нерівності трикутника також може допомогти вам знайти діапазон третьої сторони. Дві наведені сторони - 6 і 10. Третя сторона, s, повинна бути між\(10−6=4\) і\(10+6=16\). Іншими словами, діапазон значень для\(s\) є\(4<s<16\).

    F-д_22д9 ДАФ ББФ 3АЦ56АФ ФС42ДДА 13БЦК 94201КБ32Е5Д751ЕФ15А798366+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Зверніть увагу, що діапазон не менше 4, і не дорівнює 4. Третя сторона може бути 4.1 тому що\(4.1+6>10\). З тієї ж причини s не може бути більше 16, але це може\(15.9, 10+6>15.9\).

    Приклад\(\PageIndex{5}\)

    Підстава рівнобедреного трикутника має довжину 24. Що можна сказати про довжину кожної ноги?

    Рішення

    Щоб вирішити цю задачу, пам'ятайте, що рівнобедрений трикутник має дві конгруентні сторони (ноги). Треба переконатися, що сума довжин ніжок більше 24. Іншими словами\(x\), якщо довжина ноги:

    \(\begin{align*} x+x&>24 \\ 2x&>24 \\ x&>12\end{align*}\)

    Кожна ніжка повинна мати довжину більше 12.

    Рецензія

    Визначити, чи можуть набори довжин нижче скласти трикутник. Якщо ні, то вкажіть чому.

    1. 6, 6, 13
    2. 1, 2, 3
    3. 7, 8, 10
    4. 5, 4, 3
    5. 23, 56, 85
    6. 30, 40, 50
    7. 7, 8, 14
    8. 7, 8, 15
    9. 7, 8, 14.99

    Якщо задано дві довжини сторін трикутника, визначте діапазон довжини третьої сторони.

    1. 8 і 9
    2. 4 і 15
    3. 20 і 32
    4. 2 і 5
    5. 10 і 8
    6. \(x\)і\(2x\)
    7. Ніжки рівнобедреного трикутника мають довжину по 12 кожна. Що можна сказати про довжину підстави?

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 5.7.

    Ресурси

    Лексика

    Термін Визначення
    Теорема про нерівність трикутника Теорема нерівності трикутника стверджує, що для того, щоб зробити трикутник, дві сторони повинні скласти більше, ніж третя сторона.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Теорема нерівності трикутника

    Види діяльності: Питання обговорення теореми нерівності трикутника

    Навчальні посібники: нерівності в трикутниках Навчальний посібник

    Практика: Теорема нерівності трикутника

    Реальний світ: Теорема нерівності трикутника