Skip to main content
LibreTexts - Ukrayinska

4.14: САС

  1. Last updated
  2. Save as PDF
  • Page ID
    54715

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Два набори відповідних сторін і включені кути доводять конгруентні трикутники.

    Бічний кут-бічний постулат

    Якщо дві сторони і включений кут в один трикутник конгруентні двом сторонам, а включений кут в інший трикутник, то два трикутника є конгруентними. (Коли кут знаходиться між двома заданими сторонами багатокутника, він називається включеним кутом.)

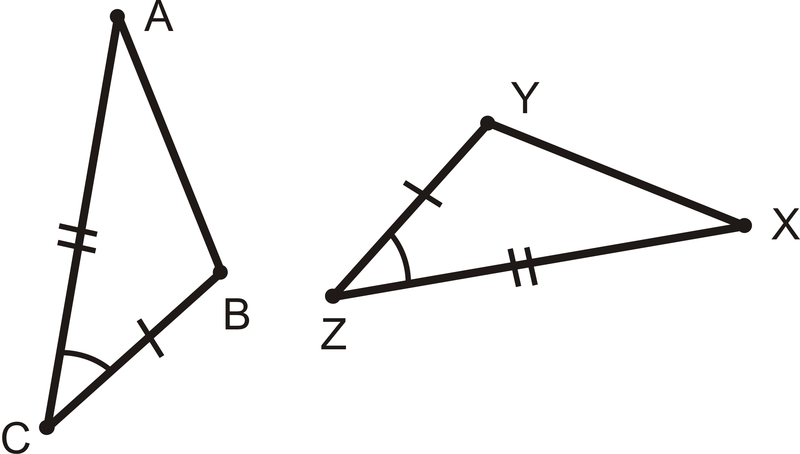
    F-D_77CA1D4D5A96259729F68 CFF 461702E9C92B5ABB6018335683FA888+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    \(\overline{AC}\cong \overline{XZ}\),\(\overline{BC}\cong YZ\), і\(\angle C\cong \angle Z\), потім\(\Delta ABC\cong \Delta XYZ\).

    Це називається Постулатом Side Angle-Side (SAS), і це ярлик для доведення того, що два трикутники є конгруентними. Розміщення слова Angle є важливим, оскільки воно вказує на те, що кут, який ви задаєте, знаходиться між двома сторонами.

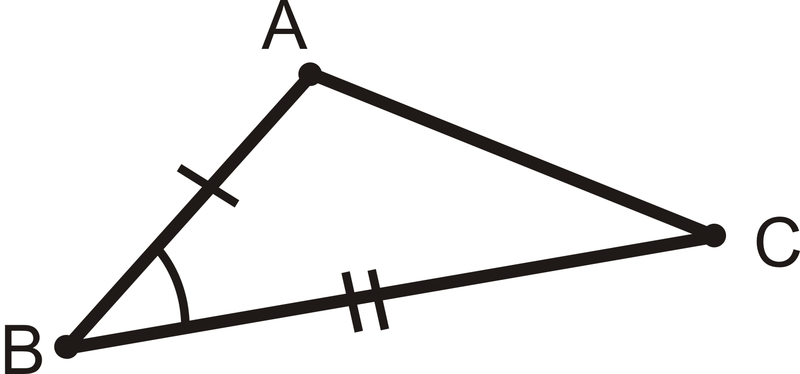
    F-D_CEE2C890Ф31Б8AE0 CAEFB7CD8C4E176F3B464AE58AECA28DB82AE6D1+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    \(\angle B\)буде включений кут для сторін\(\overline{AB}\) і\(\overline{BC}\).

    Що робити, якщо вам дали два трикутники і надали лише дві їх довжини сторін і міру кута між цими двома сторонами? Як ви могли визначити, чи два трикутники були конгруентними?

    Приклад\(\PageIndex{1}\)

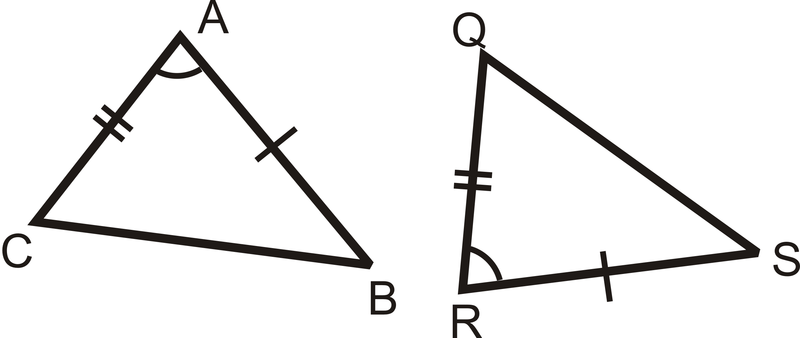
    Чи є пара трикутників конгруентна? Якщо так, напишіть заяву про конгруентність і чому.

    F-D_852448 ЕАА7Е9493Д8517А0КБ61Б8Б84 ФААА41Е910ФБДК4777А47325+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Пара трикутників конгруентна постулатом SAS. \(\Delta CAB\cong \Delta QRS\).

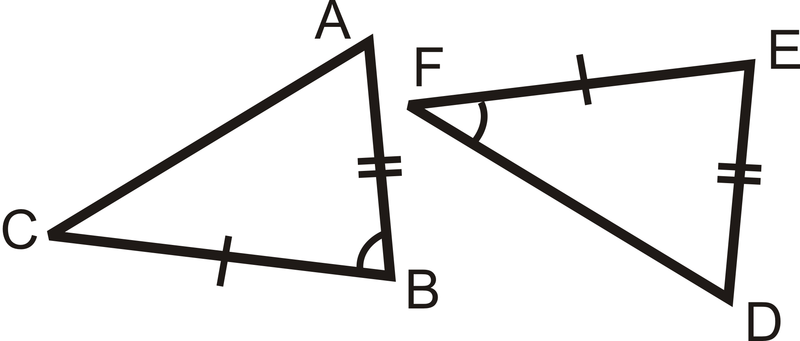
    Приклад\(\PageIndex{2}\)

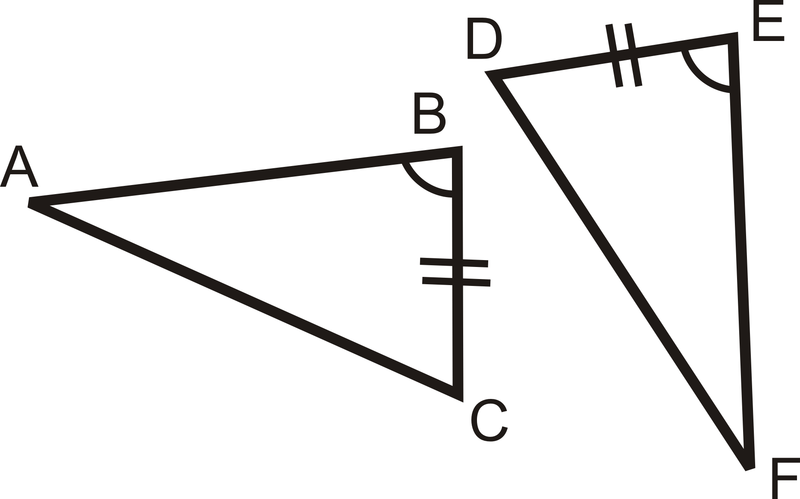
    Вкажіть додаткову інформацію, необхідну для того, щоб показати, що кожна пара трикутників є конгруентною.

    F-D_Бад 366Ф4АД 886Б8КД01Е6Д 3ФФ ФСД 17ФД 9АФ8Д300533Б9 CFB63D8D+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Ми знаємо, що одна пара сторін і одна пара кутів конгруентні з діаграми. Для того, щоб знати, що трикутники конгруентні SAS, ми повинні знати, що пара сторін на іншій стороні кута є конгруентними. Отже, ми повинні це знати\(\overline{EF}\cong \overline{BA}\).

    Приклад\(\PageIndex{3}\)

    Заповніть пропуски в доказі нижче.

    Дано:

    \(\overline{AB}\cong \overline{DC},\: \overline{BE}\cong \overline{CE}\)

    Доведіть:\(\Delta ABE\cong \Delta ACE\)

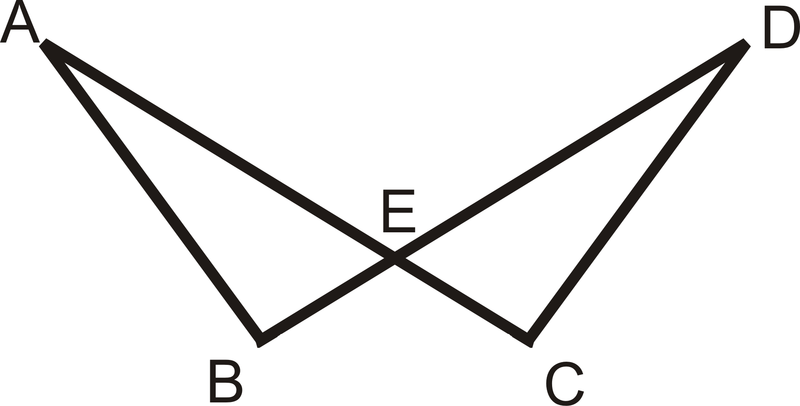
    F-D_575A2E0593763E6ФБ86А98БФ20А6Б8ФД06С9ДБКБ90С53E838A+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Заява Причина
    1. 1.
    2. \(\angle AEB\cong \angle DEC\) 2.
    3. \(\Delta ABE\cong \Delta ACE\) 3.
    Заява Причина
    1. \(\overline{AB}\cong \overline{DC},\: \overline{BE}\cong \overline{CE}\) 1. Враховується
    2. \(\angle AEB\cong \angle DEC\) 2. Теорема вертикального кута
    3. \(\Delta ABE\cong \Delta ACE\) 3. Постулат SAS

    Приклад\(\PageIndex{4}\)

    Яку додаткову інформацію вам потрібно показати, що ці два трикутники конгруентні, використовуючи Постулат SAS\(\angle ABC\cong \angle LKM\),\(\overline{AB}\cong LK\overline{AB}\),\(\overline{BC}\cong \overline{KM}\), або\(\angle BAC\cong \angle KLM\)?

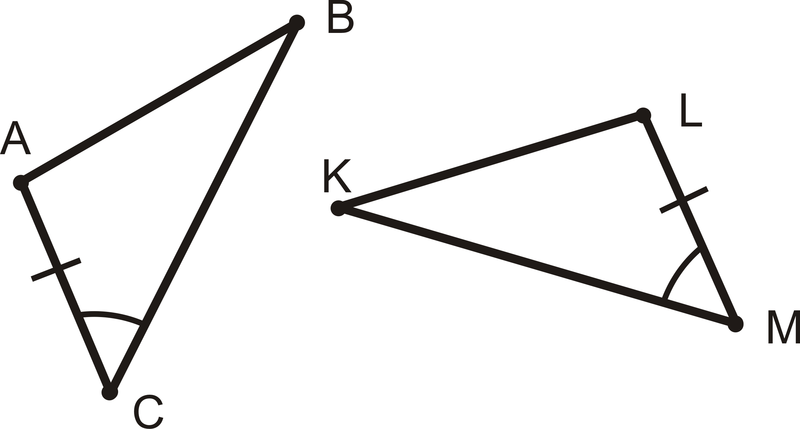
    F-D_502A8288A0AE68D09D4 АФК 39181 ФКД 57c1f33b123ed042870 в кабіному+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Для Постулату SAS потрібна сторона з іншого боку кута. В\(\Delta ABC\), тобто\(\overline{BC}\) і в\(\Delta LKM\) тому є\(\overline{KM}\). Відповідь є\(\overline{BC}\cong \overline{KM}\).

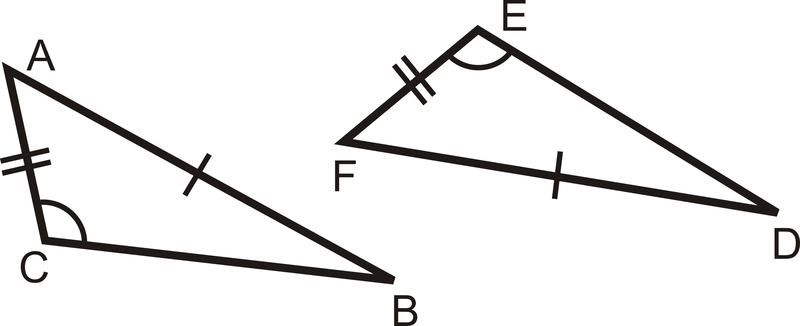
    Приклад\(\PageIndex{5}\)

    Чи є пара трикутників конгруентна? Якщо так, напишіть заяву про конгруентність і чому.

    Ф-Д_30Б11А88А9С03КБ6А693 АФБ0ФД 465ФД9Б106К8044832С43А1С9Е+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Хоча трикутники мають дві пари сторін і одну пару кутів, які є конгруентними, кут не знаходиться в одному місці в обох трикутників. Перший трикутник підходить до SAS, а ось другий трикутник - SSA. Недостатньо інформації, щоб ми знали, чи є ці трикутники конгруентними.

    Рецензія

    Чи є пари трикутників конгруентними? Якщо так, напишіть заяву про конгруентність і чому.

    1. Ф-д_а30д374А5ДА 5273АФ9Ф11Б1Ф0344К1ФЧ006Е1964А318Д0АА80А4+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
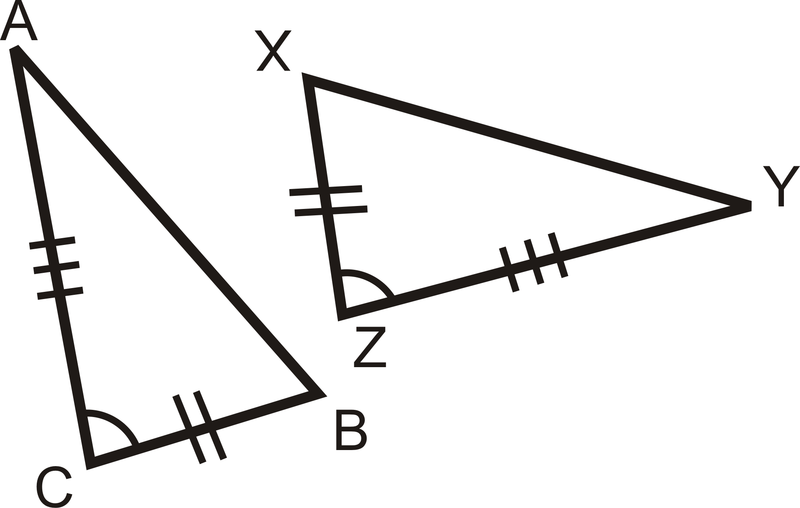
    2. F-д_дед 93С2Б13СБ 498 СБ02Б6 АЕКА 551 ЕФАД 75С28Ф15АД 011504166D0D0DF+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
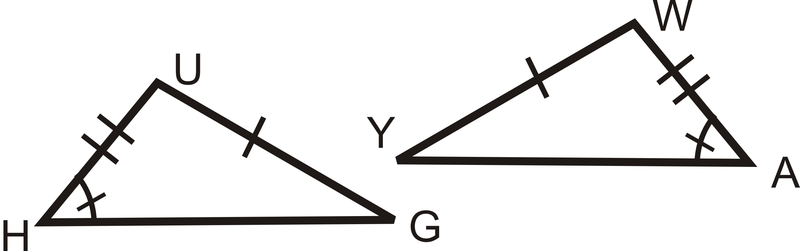
    3. F-д_17ЕФ 62378D001251FE 3259568A026 BE853Б683Е6261Д9Б554C506+зображення_крихіткий+зображення_крихіткий_png
      Малюнок\(\PageIndex{7}\)

    Вкажіть додаткову інформацію, необхідну для того, щоб показати, що кожна пара трикутників є конгруентною SAS.

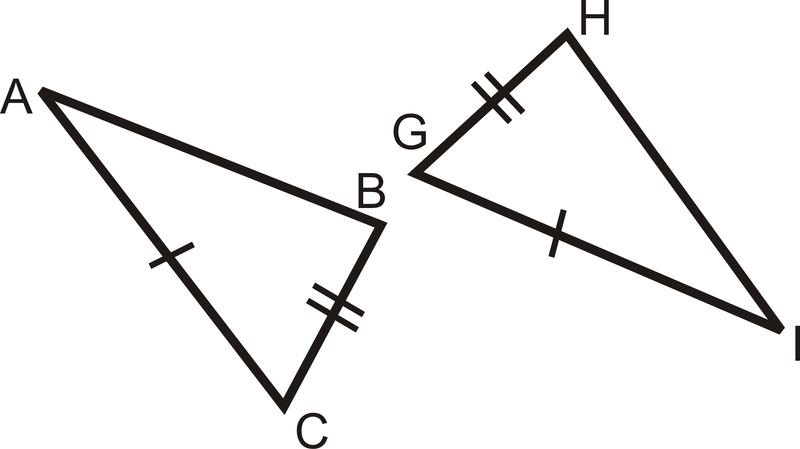
    1. F-D_241 цеб 6317Д76 CFD44148А92Б63368 ФК3С0 Ди028Ф9Б5ФК2Д6859287+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
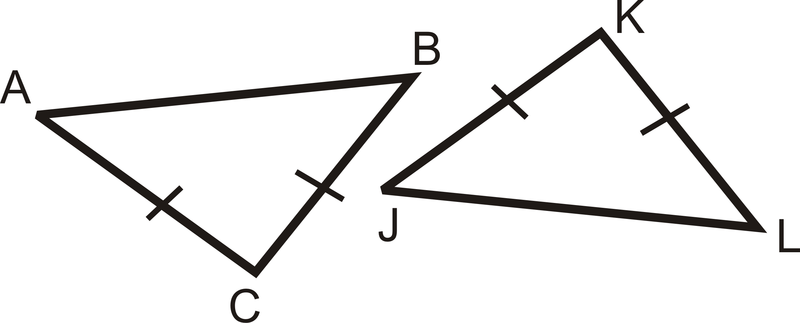
    2. F-Д_ФК 90Б95065ДААБ 8СБ558 CFF 608472А845Б94Д58Д2372BE4E0F39+зображення_крихітка_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
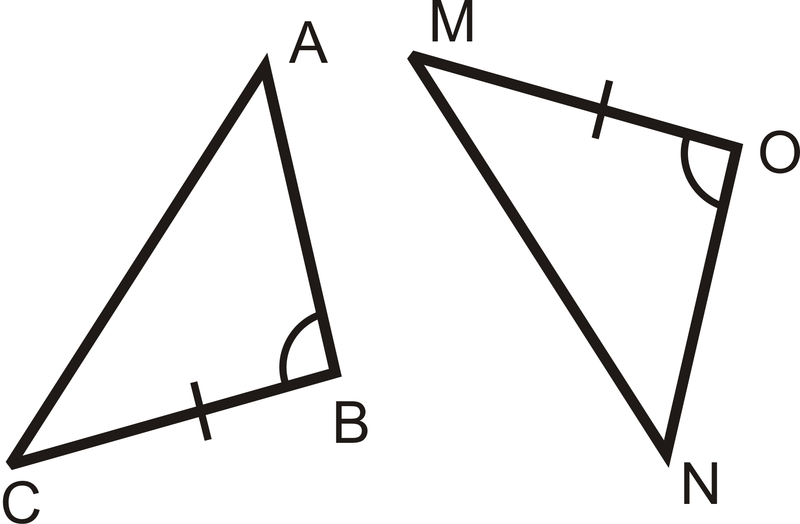
    3. F-д_AB6F7D67E291 змінного струму FF7083cd17dc65e64bfcddfdfe 85941d6d00d388ce5+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)

    Заповніть пропуски в докази нижче.

    1. Дано:
      • \(B\)є середньою точкою\(\overline{DC}\)
      • \(\overline{AB}\perp \overline{DC}\)

      Доведіть:\(\Delta ABD\cong \Delta ABC \)

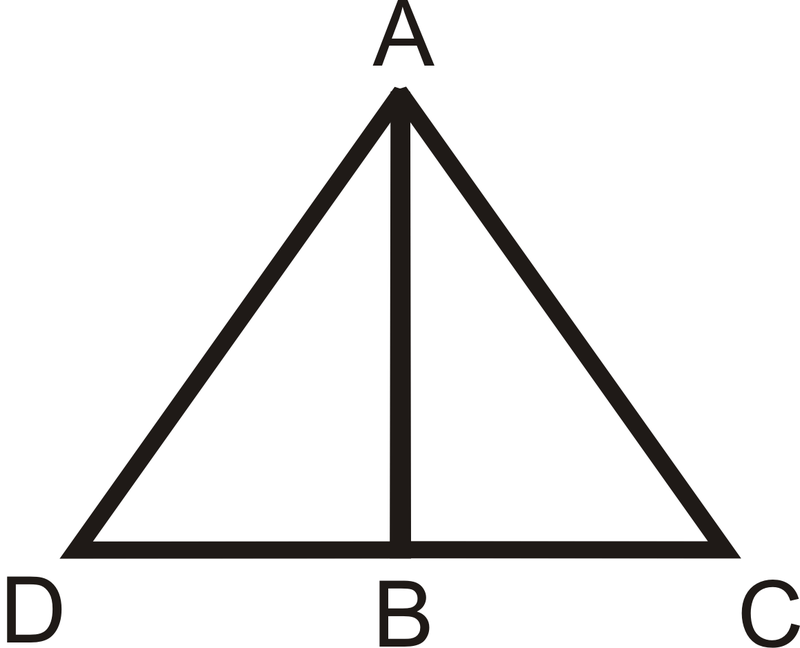
      F-D_150648577D2E3777 CAF 7E05299F91A609AC 26271341 ACD63182+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
    Заява Причина
    1. \(B\)є середньою точкою\(\overline{DC},\: \overline{AB}\perp \overline{DC}\) 1.
    2. 2. Визначення середньої точки
    3. \(\angle ABD\)і\(\angle ABC\) є прямими кутами 3.
    4. 4. Всі прямі кути є\ cong\)
    5. 5.
    6. \(\Delta ABD\cong \Delta ABC\) 6.
    1. Дано:
      • \(\overline{AB}\)є кутовою бісектрисою\(\angle DAC\)
      • \(\overline{AD}\cong \overline{AC}\)

      Доведіть:\(\Delta ABD\cong \Delta ABC \)

      F-D_150648577D2E3777 CAF 7E05299F91A609AC 26271341 ACD63182+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
    Заява Причина
    1. 1.
    2. \(\angle DAB\cong \angle BAC\) 2.
    3. 3. Рефлексивний\(PoC\)
    4. \(\Delta ABD\cong \Delta ABC\) 4.
    1. Дано:
      • \(B\)є середньою точкою\( \overline{DE}\) і\(\overline{AC}\)
      • \(\angle ABE\)є прямим кутом

      Доведіть:\(\Delta ABE\cong \Delta CBD \)

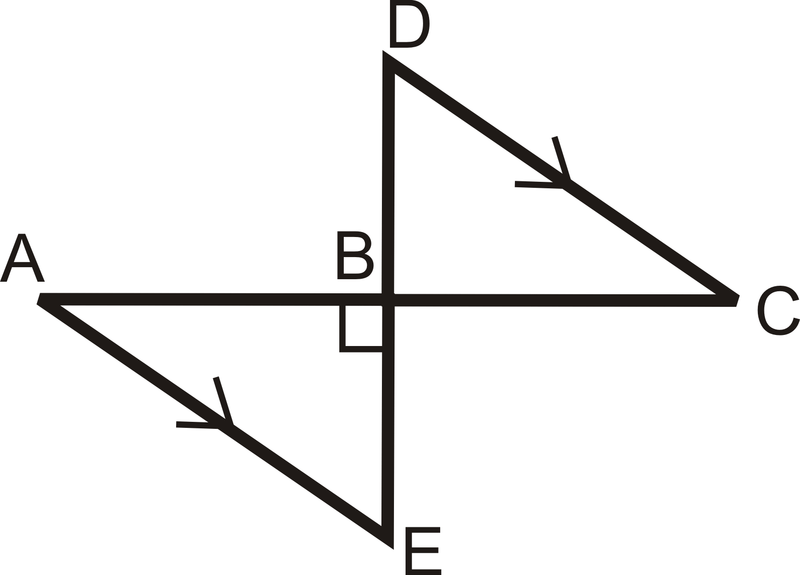
      Ф-д_Б5831Б67Д99Б1Ф53Е36С306А39698362Д66ФБК 498Ф121314055C8C65+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
    Заява Причина
    1. 1. Враховується
    2. \(\overline{DB}\cong \overline{BE},\: \overline{AB}\cong \overline{BC}\) 2.
    3. 3. Визначення прямого кута
    4. 4. Теорема вертикального кута
    5. \(\Delta ABE\cong \Delta CBD\) 5.
    1. Дано:
      • \(\overline{DB}\)є кутовою бісектрисою\(\angle ADC\)
      • \(\overline{AD}\cong \overline{DC}\)

      Доведіть:\(\Delta ABD\cong \Delta CBD\)

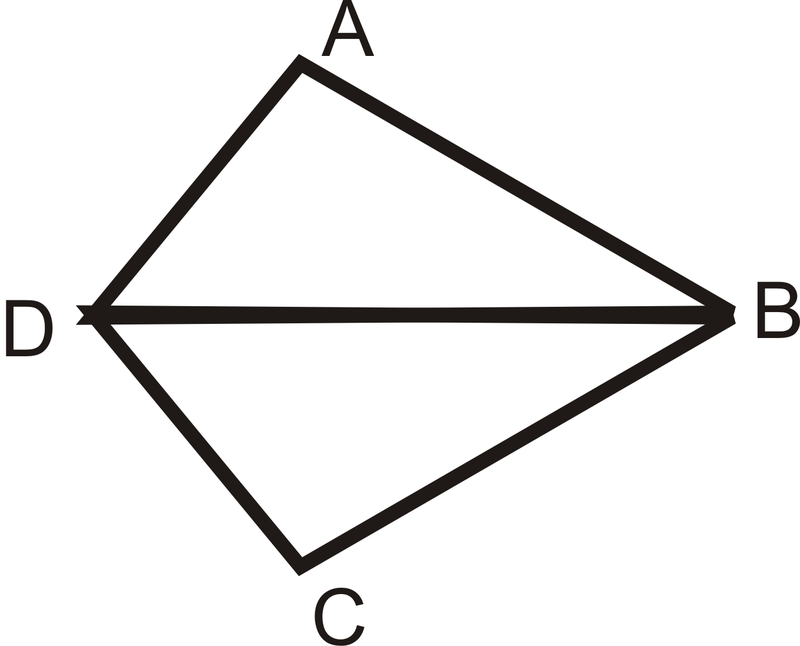
      F-D_9A6BCFD03D0BE2A3А8Б015232Ф2ЕЕ6581Д1ДД687336 BE3C5DAC 795+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
    Заява Причина
    1. 1.
    2. \(\angle ADB \cong \angle BDC\) 2.
    3. 3.
    4. \(\Delta ABD\cong \Delta CBD\) 4.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 4.7.

    Ресурси

    Лексика

    Термін Визначення
    Базові кути Базові кути рівнобедреного трикутника - це кути, утворені підставою і однією ніжкою трикутника.
    Конгруентний Конгруентні фігури ідентичні за розміром, формою і мірою.
    Рівносторонній трикутник Рівносторонній трикутник - це трикутник, у якого всі три сторони мають однакову довжину.
    У комплекті Кут Вхідний кут в трикутник - це кут між двома відомими сторонами.
    SAS SAS означає сторону, кут, сторону, і відноситься до того, що дві сторони і включений кут трикутника відомі.
    Бічний кут бічного трикутника Бічний кут бічний трикутник - це трикутник, де дві сторони і кут між ними відомі величини.
    Конгруентність трикутника Конгруентність трикутника виникає, якщо 3 сторони в одному трикутнику конгруентні 3 сторонам в іншому трикутнику.
    Жорстке перетворення Жорстке перетворення - це перетворення, яке зберігає відстань і кути, воно не змінює розмір або форму фігури.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Вступ до конгруентних трикутників

    Діяльність: Питання обговорення конгруентності трикутника SAS

    Навчальні посібники: Посібник з вивчення конгруентності три

    Практика: SAS

    Реальний світ: Конгруентність трикутника SSS